Презентация на тему: Решение линейных уравнений, содержащих неизвестное под знаком модуля

Решение линейных уравнений, содержащих неизвестное под знаком модуля Чернова Галина Петровна учитель математики 1 категории«СОШ №4» г. Новочебоксарска

ЦЕЛЬ РАБОТЫРассмотреть примеры уравнений, содержащих неизвестное под знаком модуля с точки зрения геометрического смысла модуля и алгебраического определения модуля.Научиться применять эти методы при решении уравнений, содержащих неизвестное под знаком модуля.

Этапы работы над проектом:Теоретическая часть работы.Исследовательская проблема.Практическая часть работы.Итог работы.

Теоретическая основа проекта.Именно математика даёт надёжные правила: кто им следует- тому не опасен обман чувств Л. Эйлер

Любое действительное число можно изобразить точкой на числовой прямой.Расстояние этой точки от начала отсчета на этой прямой равноположительному числу или нулю, если точка совпадает с началом числовой прямой Расстояние от начало отсчета до точки, изображающей данное число на числовой прямой, называется модулем этого числа.Модуль числа а обозначается ׀а ׀

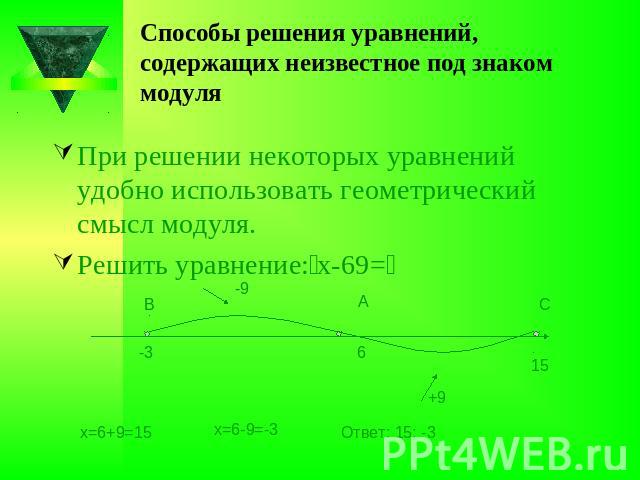
Способы решения уравнений, содержащих неизвестное под знаком модуляПри решении некоторых уравнений удобно использовать геометрический смысл модуля.Решить уравнение:׀х-6׀=9

Способы решения уравнений, содержащих неизвестное под знаком модуля.При решении уравнений, содержащих несколько выражений под знаком модуля, удобнее пользоваться алгебраическим определением модуля:Модулем положительного числа и нуля является само число; модулем отрицательного числа является противоположное ему положительное число.

Решите уравнение:׀2х-12׀+׀6х+48׀=160Решение:Найдём корни(нули) каждого выражения, содержащего знак модуля: 2х-12=0 6х+48=0 х=6 х=-8б) найденные значения х разбивают числовую прямую на три промежутка:в)решение данного уравнения рассматриваем в каждом промежутке отдельно:

х<-8в этом промежутке оба неравенства, стоящие под знаком модуля, отрицательны.

-8≤х≤6в данном промежутке первое выражение, стоящее под знаком модуля, отрицательно, а второе – положительно.число 25 не принадлежит данному промежутку

х>6оба выражения, стоящие под знаком модуля, положительныОтвет: -24,5 ; 15,8

Решение уравнений.

Проверим вместе:Ответ: -4; 10Ответ: -17; 22

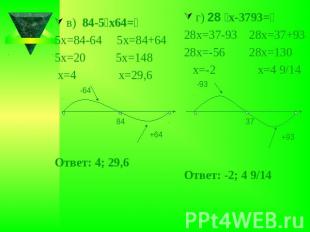
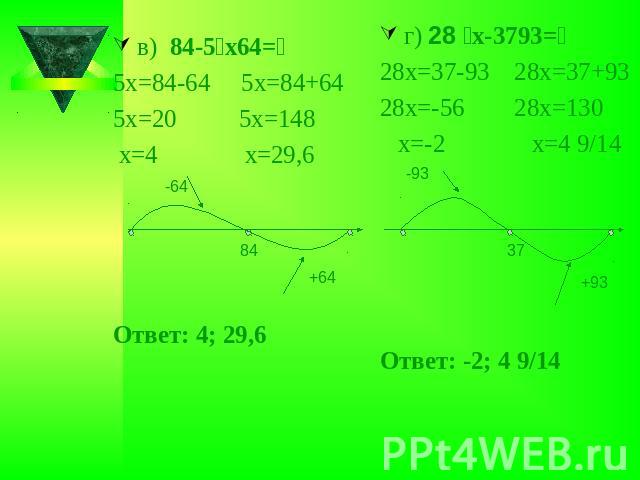
Ответ: 4; 29,6Ответ: -2; 4 9/14

Ответ: -10 ¹/¹¹; 5 4/7

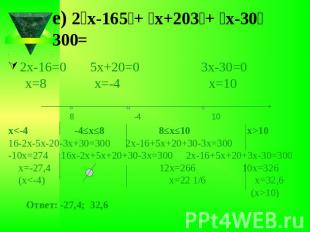
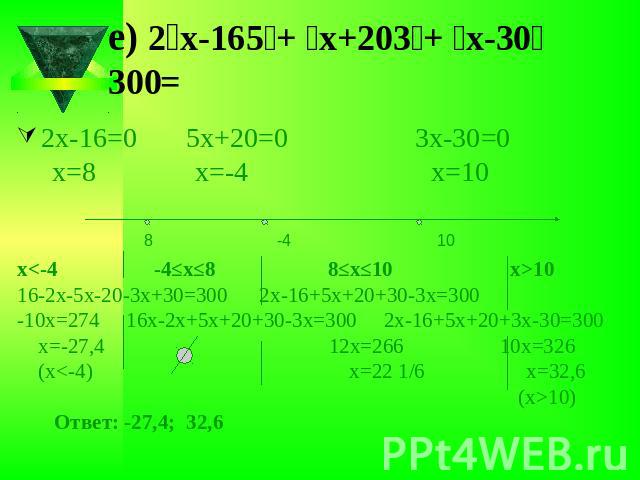
е) ׀2х-16׀+ ׀5х+20׀ +׀3х-30׀ =3002х-16=0 5х+20=0 3х-30=0 х=8 х=-4 х=10х<-4 -4≤х≤8 8≤х≤10 х>1016-2х-5х-20-3х+30=300 2х-16+5х+20+30-3х=300-10х=274 16х-2х+5х+20+30-3х=300 2х-16+5х+20+3х-30=300 х=-27,4 12х=266 10х=326 (х<-4) х=22 1/6 х=32,6 (х>10) Ответ: -27,4; 32,6

15х-105=0 12х-288=015х=105 12х=288 х=7 х=24 х<7 7≤х≤24 х>24105-15х-12х+288=536 15х-105-12х+288=536 15х-105+12х-288=536 -27х=142 3х=353 27х=928 х=-5 8/27 х=117 2/3 х=34 10/27 (х <7) (х>24)Ответ: -5 8/27; 34 10/27

з)׀36-12х׀-׀5х+20׀-׀7х-35׀=240х<-4 -4≤х≤ 3 3≤х≤ 5 х>5-12х+36 -12х+36 12х-36 12х-36+ 5х-20 -5х-20 -5х-20 -5х-20+ 7х-35 +7х-35 +7х-35 -7х +350х=240 -10х=259 14х=331 0х=240 х=-25,9 х=23 9/14Ответ: нет решения

Подведём итог работыИспользуя два смысла модуля: геометрический и алгебраический, мы научились решать уравнения, содержащие неизвестные под знаком модуля и закрепили это на примерах.