Презентация на тему: Решение систем двух линейных уравнений с двумя переменными различными способами

Решение систем двух линейных уравнений с двумя переменными различными способами учитель математики МОУ «Средняя школа №12» Кузнецова Т. Н.

Цель урока: Продолжить формирование навыков сознательного выбора способа решения системы Развивать потребность в нахождении рациональных способов решения Воспитывать умение контролировать внимание на всех этапах урока

Психологическая установка учащимся 1. Продолжаем отрабатывать навыки решения систем уравнений; продолжаем учиться решать; формируем математическую интуицию, которая поможет ориентироваться в способах решения систем. 2. На уроке можно ошибаться, сомневаться, консультироваться. 3. Дать самому себе установку: «Понять и быть тем первым, который увидит ход решения».

I. Проверка домашнего задания В каком виде чаще всего нам предлагается запись системы линейных уравнений? а1х + b1y = c1 а2х + b2y = c2 2. Какова связь между коэффициентами? Если а1/а2=b1/b2≠c1/c2 Нет решений Если а1/а2=b1/b2=c1/c2 Много решений Если а1/а2≠b1/b2≠c1/c2 Единственное решение

Вопрос: Установите связь между коэффициентами: а) 6x – 5y = 4, б) 3х – у = 5, в) х – у = 3, 12x – 10y = 5; 12х – 4у = 20; 3х + у = а) 6/12 = -5/(-10)≠4/5 не имеет решения б) 3/12 = -1/(- 4) = 5/20 бесчисленное множество решений в) 1/3 ≠ -1/1≠3/5 одно решение

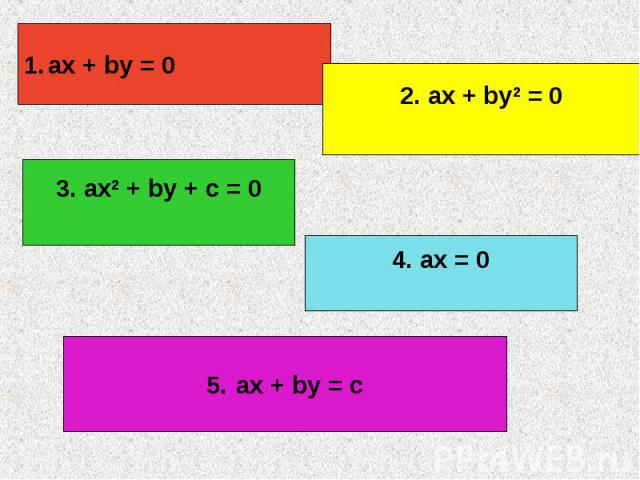
II. Повторение пройденного материала Закончи определение: «Линейным уравнением с двумя переменными называется уравнение вида…»

Сколько вы изучили способов решения системы линейных уравнений?

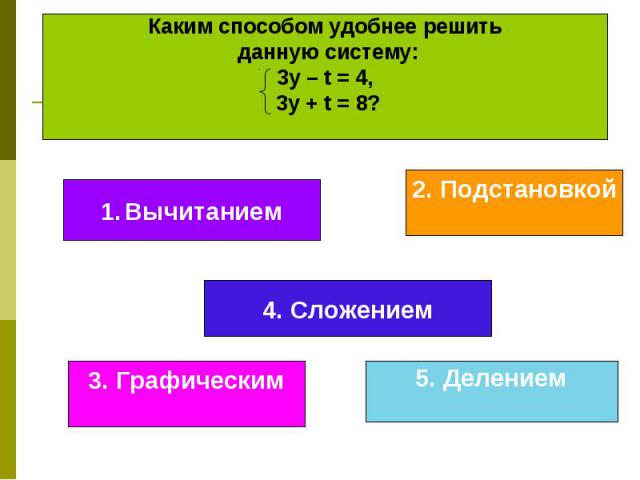
Каким способом удобнее решить данную систему: 3у – t = 4, 3у + t = 8?

Выберите систему линейных уравнений, удовлетворяющих условию: сумма чисел равна 81, а их разность равна 15. а) у + х = 15, б) х + 81 = у, в) х – 15 = у, у– х = 81. х - у = 15. х + у = 81. г) х + у = 81, д) х – 15 = у, х – у = 15. х + 81 = у. в), г)

Выразите одну переменную через другую 1. 4х – у = 3 у = 4х – 3 2. – 6х + 2у = 1 у = 3х + 1 3. 0,5х – 3,5у = 7 х = 14 + 7у 4. – а/6 – 2b= -6 а = 36 + 12b 4. Х + (2у)/5 = -3 х = -0,6 – 0,4у 5.Х/15 + у/12=0 у = - 0,8

III. Решить систему уравнений 2х + у = 5, 3х + 4у = 10. (2; 1) 2. у – х = 0, 3х + у = 8. б) (2;2)

IV. Самостоятельная работа Найдите решение системы уравнений: Уровень «А» Уровень «B» а) У=3х, а) 4х – у = 9, 4х + 5у = 38. 3х + 7 = -1. б) 2х – у = 2, б) 3х – у = 7, 3х + у = 8. 2х + 3у = 1 Уровень «С» а) 2х – у = 4, 3х + 7 = 6. б) 5х + 3у = -2, 7х – 4у = 30.

Самопроверка Уровень «А» а) (2;6) б) (2;2) Уровень «B» а) (2; - 1) б) (2 ; -1) Уровень «С» а) (2;0) б) (2; - 4)

VIII Домашнее задание: № 1163, №1168(а), № 1172(а) П 42-44 повторить.

Подведение итогов урока В каком виде чаще всего предлагается запись систем линейных уравнений? Какова связь между коэффициентами? Уравнение какого вида называется линейным уравнением с двумя переменными? Сколько вы изучили способов решения систем линейных уравнений?  

Спасибо за внимание!