Презентация на тему: Объем прямоугольного параллелепипеда 11 класс

МОУ «Средняя общеобразовательная школа с. Погорелка Шадринский район Курганская областьОБЪЕМ ТЕЛУчитель математики первой квалификационной категории Кощеев М.М.

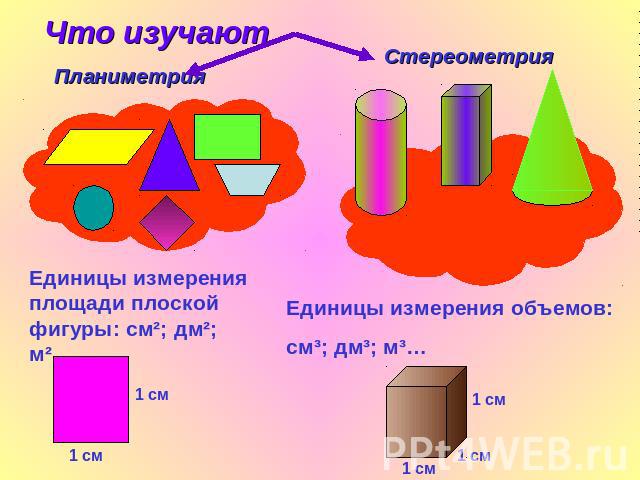
ПЛОСКИЕО БЪЕМНЫЕ

ПЛОСКИЕ ФИГУРЫТРЕУГОЛЬНИККВАДРАТПРЯМОУГОЛЬНИККРУГЧЕТЫРЕХУГОЛЬНИК

КУБЦИЛИНДРПАРАЛЛЕПИПЕД

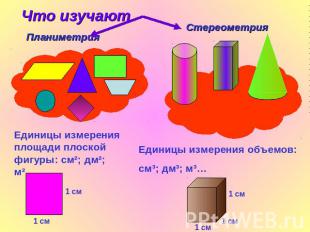
Единицы измерения площади плоской фигуры: см²; дм²; м²…Единицы измерения объемов:см³; дм³; м³…

Объем прямоугольного параллелепипеда

Цель урока:Усвоить понятие объёма пространственной фигуры;Запомнить основные свойства объёма;Узнать формулы объёма прямоугольного параллелепипеда и прямоугольной призмы.

Чтобы найти объём многогранника, нужно разбить его на кубы с ребром, равным единице измерения.

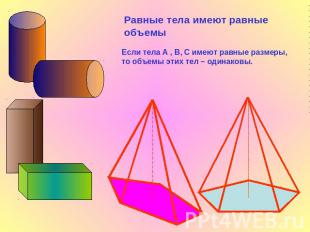
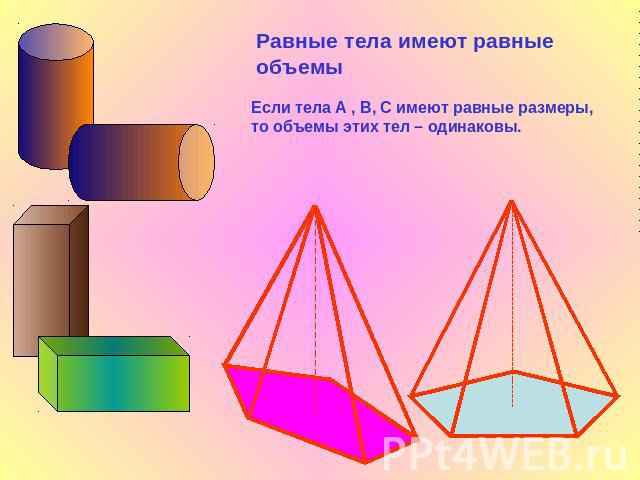
Равные тела имеют равные объемыЕсли тела А , В, С имеют равные размеры, то объемы этих тел – одинаковы.

Если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей.

Напомним формулу объёма прямоугольного параллелепипеда.

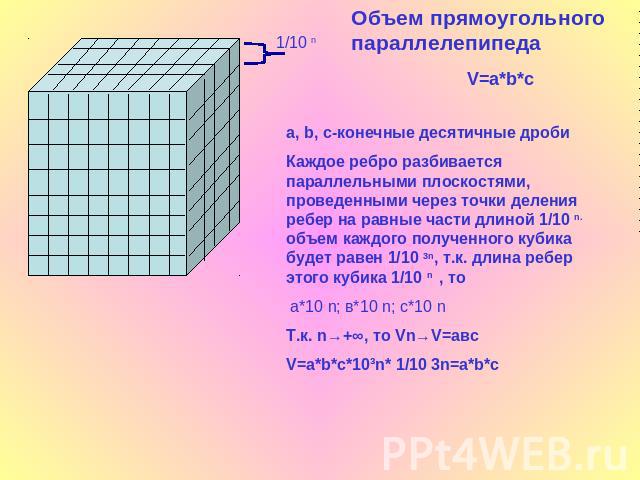
Объем прямоугольного параллелепипедаa, b, c-конечные десятичные дробиКаждое ребро разбивается параллельными плоскостями, проведенными через точки деления ребер на равные части длиной 1/10 n. объем каждого полученного кубика будет равен 1/10 3n, т.к. длина ребер этого кубика 1/10 n , то а*10 n; в*10 n; с*10 nТ.к. n→+∞, то Vn→V=авсV=a*b*c*10³n* 1/10 3n=a*b*c

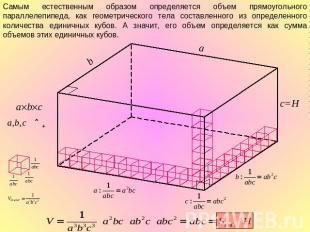
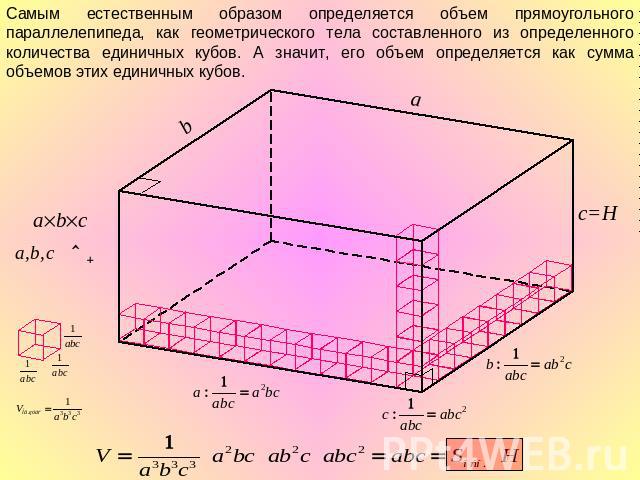
Самым естественным образом определяется объем прямоугольного параллелепипеда, как геометрического тела составленного из определенного количества единичных кубов. А значит, его объем определяется как сумма объемов этих единичных кубов.

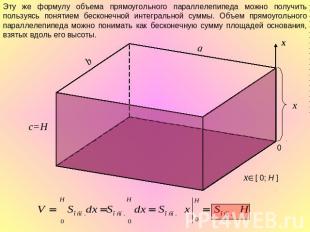
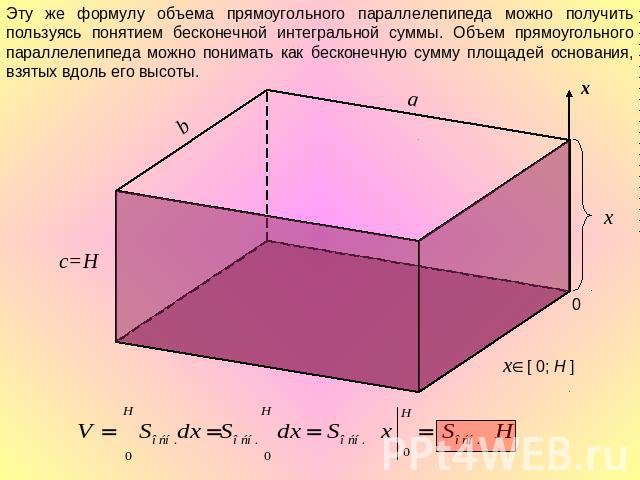
Эту же формулу объема прямоугольного параллелепипеда можно получить пользуясь понятием бесконечной интегральной суммы. Объем прямоугольного параллелепипеда можно понимать как бесконечную сумму площадей основания, взятых вдоль его высоты.

Построим сечение прямоугольного параллелепипеда , проходящее через диагонали верхнего и нижнего основанийСледствие 1: Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.V=Soc*h, т.к. Sос.=a*b;h=cСледствие 2: Объем прямой призмы, основанием которой является прямоугольный треугольник равен произведению площади основания на высоту.Т.к. ∆ABD-1/2 □АВСД→SABD=½SABCD→VABC=½SABCД*h==SABD*h

Понятие объема.Понятие объема в пространстве вводится аналогично понятию площади для фигур на плоскости.Определение 1.  объемом тела называется положительная величина, характеризующая часть пространства, занимаемую телом, и обладающая следующими свойствами: равные тела имеют равные объемы; при параллельном переносе тела его объем не изменяется; если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей; за единицу объема принят объем куба, ребро которого равно единице длины;Определение 2.  Тела с равными объемами называются равновеликими. Из свойства 2 следует, что если тело с объемом V1 содержится внутри тела с объемом V2, то V1 < V2.

№647 б) Тело R состоит из тел Р и Q, имеющих соответственно объемы V1, V2. Выразить объем V тела R через V1 V2 если б) тела Р и Q имеют общую часть, объем которой равен 1/3V1

№ 648 а), Найти объем прямоугольного параллелепипеда, стороны основания которого равны а и b, а высота равна h, если а=11, b=12, h=15

Решение: Пусть ребро куба равно а, тогда из треугольника АДС АС2=а2+а2=2а2, Рассмотрим треугольник АСС1, найдем АС1

№ 651 Кирпич имеет форму прямоугольного параллелепипеда с измерениями 25см, 12см и 6,5см. Плотность кирпича равна 1,8г/cм3. Найти его массу.

№ 658 Найдите объем прямой призмы АВСА1В1С1, если <ВАС=900, ВС=37см, АВ=35см, АА1=1,1дмДано: АВСА1В1С1- прямая призма. <ВАС=900 ВС=37см, АВ=35см, АА1=1,1дм

Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.

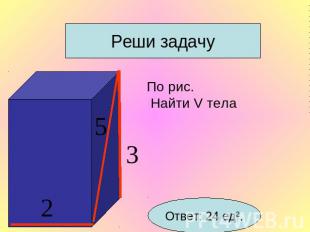
По рис. Найти V тела

Домашнее задание Домашнее заданиеП. 74, 75, № 656, 658, 648, 649

БиблиографияЛ.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев «Геометрия, 10-11», М., Просвещение, 2007В.Я. Яровенко «Поурочные разработки по геометрии», Москва, «ВАКО», 2006