Презентация на тему: Происхождение обыкновенной дроби

Происхождение обыкновенной дроби Выполнила Гертнер Элизабет 6 «В» классРуководитель Федорова Е.Ю.

Цель работы: выяснить происхождение обыкновенной дроби

Обыкновенная дробь Правильная дробь Смешанное число: числитель знаменатель Неправильные дроби

Древние математические документы Кожаный свиток г.Фивы 1700гг. Папирус Ринда написан (1849-1801г. до н.э.), переписан писцом Ахмесом (1788-1580г. до н.э.) Клинописные тексты Вавилона , вырезанные в камне 668-626гг. до н.э. «Математика в девяти книгах» Чжан Цан II в. до н.э.

Появление первых словесных дробей-долей: «Половина», «десятина», «осьмина», «ломаная»…Простейшие дроби: 1/2, 1/4, 2/3, 3/4 описывали больше качество предмета, чем его количество в старом китайском языке: 1/3- «меньшая половина», 2/3- «большая половина» На Руси винная мера: ведро=2 полведра, полведра=2 четверти; «десятина», «осьмина» - земельная мера площади половина четверти как земельной меры обозначалась словом осьмина Нельзя было сказать «осьмина книги» или «полведра пути»у римлян асс первоначально - 1/12 денежно-весовой единицы 3/12 …….. 3 унции = четверть 4/12 ……..4 унции = треть 6/12……...6 унций = половинав вавилонской системе символы 1/2, 1/3, 2/3 являлись изображением сосудовВ Египте единицей площади был сетат (квадрат со стороной 100локтям)1/4 сетата называлась «ломаной» Абстрактное понятие дроби: 1/2, 1/10,1/8, 1/4

ЕГИПЕТ все документы содержат только единичные дроби Под знаком ставили символ, изображающий знаменатель Индивидуальных знаки Кожаный свиток- ключ к пониманию первых стадий вычислений с дробями 2/5=1/5+1/15, 2/21=1/14+1/422/13=1/8+1/52+1/104 2/83=1/60+1/332+1/415+1/498

ВАВИЛОН ПРИМЕНЯЛИ ШЕСТИДЕСЯТЕРИЧНЫЕ ДРОБИ денежная и весовая единицы измерения разделялись на 60 равных частей:10талант = 60 мин, 1 мина =60 шекель. Доли шестидесятые были привычны для вавилонян: 1/60, 1/3600, 1/603В Вавилоне письменная шестидесятеричная нумерация состояла из двух знаков: ▼ – значение 1 «единица», 60, 602, 603… определялось по содежанию задачи. ◄ -10 «десять»Число 62 писали: ▼ ▼▼ с пробелом. Сохранилось деление часа на 60 минут, минуты на 60 секунд, окружности на 360 градусов, градусы на 60 минут, минуты на 60 секунд

Рим Римляне пользовались только конкретными двенадцатеричными дробями. Асс - единица измерения веса, а также денежной единица. Асс делился на 12 равных частей. Каждая часть называлась унция. унция делилась: 2 семунции, 4 сициликуса, 6 секстул, 24 скрупула и144силиквы Слово скрупулёзность произошло от «скрупула», означает точность и акуратность (например, в английском прилагательное скрупулёзный — scrupulous, во французском — scrupuleux).

Греция Греки употребляли египетские и шестидесятеричные дроби. К V в. до н.э. греки умели производить все действия с дробями, но числами их не признавали. Сначала дроби выражали словами, позднее стали применять записи:Герон и Диофант (ок. I в.) употребляли дробную черту, но сверху писали знаменатель, а под чертой – числитель. Например, 5/3 означало три пятых В греческих сочинениях по математике дробей не встречалось. Греческие математики создали учение об отношениях величин, о равенстве таких отношений. Правильное соотношение размеров возводимых ими дворцов и храмов придавало этим зданиям ту необыкновенную красоту, которая и сегодня восхищает нас. В Древней Греции получают своё начало обыкновенные дроби и впервые происходит расширение множества целых чисел.

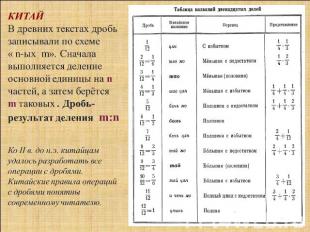
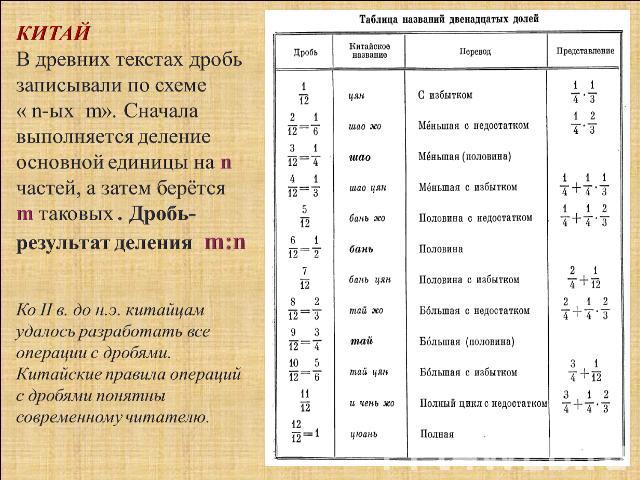
КИТАЙ В древних текстах дробь записывали по схеме « n-ых m». Сначала выполняется деление основной единицы на n частей, а затем берётся m таковых . Дробь-результат деления m:nКо II в. до н.э. китайцам удалось разработать все операции с дробями. Китайские правила операций с дробями понятны современному читателю.

Индия В Индии дроби известны очень давно. Ещё в середине II тысячелетия до н.э. упоминаются такие дроби как 1/2, 3/4, 1/16 Индийцы записывали дроби так, как это делается в настоящее время: числитель над знаменателем, только без дробной черты. Друг от друга дроби отделялись вертикальными и горизонтальными линиями. Дробь записывалась: в смешанной дроби целая часть писалась над дробью. Индийцы развили теорию обыкновенной дроби. Обыкновенные дроби индийцев наряду с египетскими единичными и вавилонскими шестидесятеричными перешли к арабам.

ИСЛАМ Дроби в арабской математике считались такими же числами, как и натуральные числа. Записывали их вертикально, как индийцы: знаменатель под числителем, целую часть писали над числителем черта дроби появилась около 1200 года Арабский язык не имеет специальных терминов для выражения долей единицы (единичных дробей) меньших 1/10 (1/100, 1/1000..) Такие результаты округляли. Понятия конкретной дроби: одна или несколько частей величины предполагаемой делимой (единица считалась неделимой) называются « одна часть из n», отношение двух отвлечённых чисел. «m частей из » Главная историческая заслуга математиков исламских стран — сохранение античных знаний (совместно с более поздними индийскими открытиями) и содействие тем самым восстановлению европейской науки.

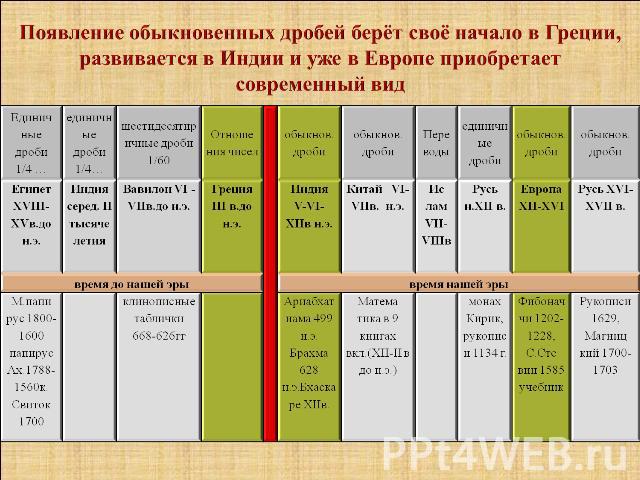
ЕВРОПА Учение о дробях считалось самым трудным разделом арифметики. Трудность изучения дробей в средневековых школах объяснялась тем, что учеников заставляли заучивать без понимания Первым самостоятельным математиком Западной Европы был итальянец Леонардо Пизанский (1180-1240), известный под именем Фибоначчи (сын Боначчи). В конце ХII века он изучал математику у арабских учителей, посещал Египет, Сирию, Византию, Сицилию. Основной труд Леонардо – книга «Книга абака» («Книга арифметики» 1202-1228г.) В ней он учит действию над смешанными числами и дробями . Вводит«дробь» вместо «ломаной», применяет постояннодробную черту. Теория обыкновенных дробей берёт своё начало в Греции, развивается в Индии и уже в Европе приобретает современный вид.

На РУСИ 1/4 – четь1/2 - половина, полтина1/8 – полчеть1/16 – полполчеть1/32 – полполполчеть (малая четь)1/7 – седимина   1/3 – треть1/6 – полтреть1/12 – полполтреть1/24 – полполполтреть (малая треть)1/5 – пятина1/10 - десятина5/13 – пять тринадцатых жеребёв Термины в рукописях ХVII столетия назывались так: делимое – « большой перечень»делитель – «деловой перечень»частное – «жеребейный перечень»остаток – «остаточная доля»2 1/2 – «полтретьи», 4 1/2- «полпяты» Числитель назывался верхним числом, а знаменатель исподним Леонтий Филиппович Магницкий «Арифметика, сиречь наука численная» 1700-1703гг. Послужила проводником в Россию новых математических сведений, совершенно не имеющихся в существовавших до неё рукописях.

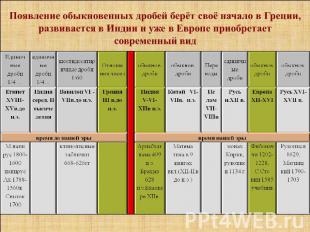
Появление обыкновенных дробей берёт своё начало в Греции, развивается в Индии и уже в Европе приобретает современный вид

Современный вид обыкновенной дробиТермин ввёл в 1558 г. Траншан для отличия дроби a/b от астрономических дробей Вертикальная запись: Индия, КитайДробная черта, «Дробь» : Л. Пизанский 1202-1228гг.Солидус: наклонная дробная черта «Дробь» -Число, представленное как состоящее из частей единицы.(С.И. Ожегов)fraction ['frækʃ(ə)n]англ.яз. (дробь, доля, порция, часть, относительное количество, дробное число) 2/9«солидус» косая чертаВвёл де Морган в 1558г. Числитель Англ. numerator ['njuːm(ə)reɪtə] с латинского (numerare — числить, считать ЗнаменательАнгл.denominator [dɪ'nɔmɪneɪtə] с латинского dē-nōmino именовать, называть