Презентация на тему: Представление числовой информации с помощью систем счисления

Автор: Кузнецова Лариса Леонидовна, учитель информатики I категории. Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №10» Иркутская область, г. Байкальск Представление числовой информации с помощью систем счисления Урок информатики в 10 классе

Задачи урока Сформировать у учащихся понятие системы счисления, позиционной и не позиционной системы счисления. Сформировать у учащихся понятие основание системы счисления, разряда, свёрнутой и развёрнутой формы записи числа. Научить записывать числа в свёрнутой и развёрнутой форме записи.

Актуализация знаний Какая информация является числовой? Что используется для записи количества объектов? С помощью чего можно записать числовую информацию?

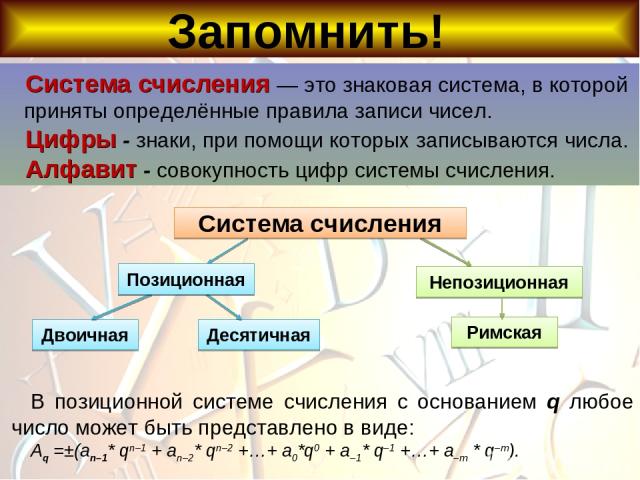
Система счисления - это знаковая система, в которой приняты определённые правила записи чисел. Цифры - знаки, при помощи которых записываются числа. Алфавит системы счисления - совокупность цифр. Запись в тетрадь

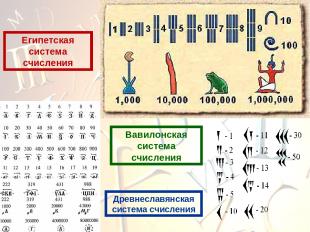
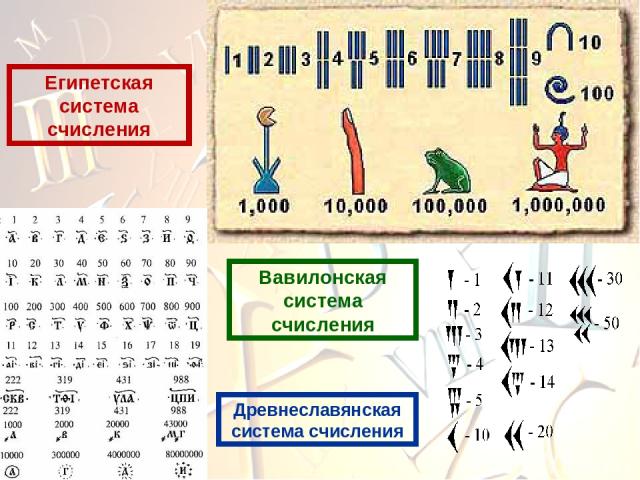
Древнеславянская система счисления Вавилонская система счисления Египетская система счисления

Непозиционные (количественное значение цифры не зависит от её положения в числе) 721 Позиционные (количественное значение цифры зависит от её положения в числе) 217 Виды систем счисления

Непозиционные системы счисления Единичная Римская

Единичная система счисления Простейшая и самая древняя система, для записи любых чисел используется всего один символ - палочка, узелок, зарубка, камушек. Позже, для облегчения счета, эти значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Непозиционные системы счисления

Римская система счисления Римская система счисления имеет свое собственное оригинальное начертание цифр. В этой системе отсутствует нуль. Римская система основана на употреблении семи особых знаков - римских цифр, которые делятся на четыре знака десятичных разрядов I = 1, X = 10, C = 100, M = 1000 и три знака половин десятичных разрядов V = 5, L = 50, D = 500.

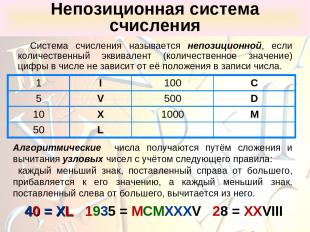
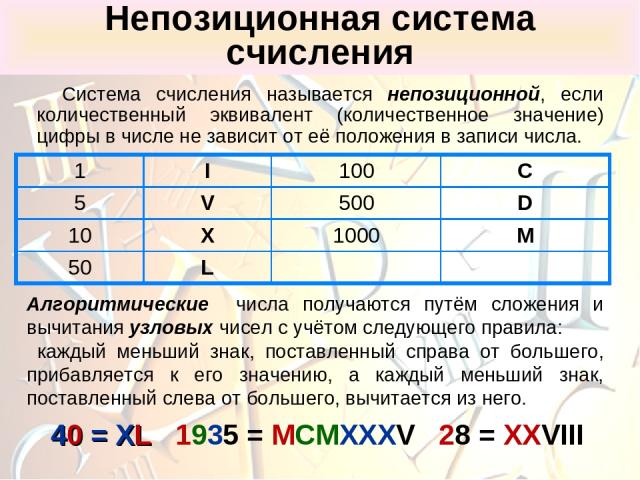
Непозиционная система счисления Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа. Алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него. 40 = XL 1935 = MCMXXXV 28 = XXVIII 1 I 100 C 5 V 500 D 10 X 1000 M 50 L

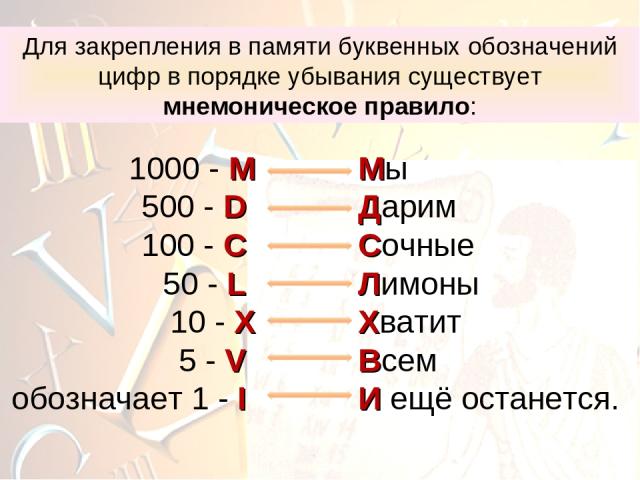
Для закрепления в памяти буквенных обозначений цифр в порядке убывания существует мнемоническое правило: 1000 - M 500 - D 100 - C 50 - L 10 - X 5 - V обозначает 1 - I Мы Дарим Сочные Лимоны Хватит Всем И ещё останется.

Запись римскими цифрами Натуральные числа, т. е. целые положительные числа (без нуля), можно записывать при помощи повторения римских цифр, используя четыре следующих правила: Правило 1. Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц. Пример: число 1988. Одна тысяча M, девять сотен CM, восемьдесят LXXX, восемь VIII. Запишем их вместе: MCMLXXXVIII.

Правило 2. Правило сложения: если все цифры в числе по значению не возрастают, если считать слева направо, то они складываются. Например: II = 2, VI = 6, XI = 11 - правильно, IV = 6, XL = 60 - неправильно. Запись римскими цифрами

Правило 3. Правило вычитания: сначала во всех парах, где меньшая цифра стоит перед большей, вычитается меньшая цифра из большей; затем полученные результаты вместе с оставшимися цифрами подпадают под принцип сложения и складываются. Например: IV = 4, XIV = 14, XXIX = 29 — правильно, IVX = 6, IXX = 1 — неправильно. Запись римскими цифрами

Правило 4. Ограничения: Число записывается слева направо максимально возможными цифрами; но четыре одинаковых десятичных знака подряд заменяются этим десятичным и следующим половинным; но если при этой замене этот десятичный знак оказывается между двумя одинаковыми половинными, то эти три знака заменяются этим десятичным и следующим десятичным (т. е. два половинных знака заменяются равноценным десятичным). Например: 4 = IV, а не IIII; 9 = IX, а не VIIII или VIV; 19 = XIX, а не XVIIII или XVIV. Запись римскими цифрами

Недостатки непозиционных систем счисления: для записи больших чисел необходимо вводить новые цифры (буквы); трудно записывать большие числа; нельзя записать дробные и отрицательные числа; нет нуля; очень сложно выполнять арифметические операции. Виды систем счисления

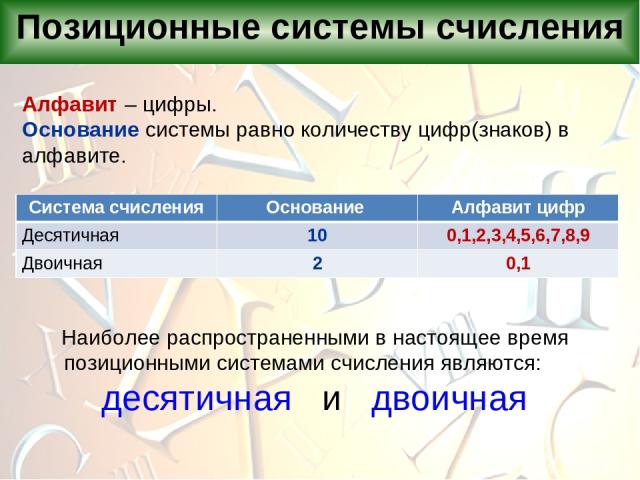
Позиционные системы счисления Алфавит – цифры. Основание системы равно количеству цифр(знаков) в алфавите. Наиболее распространенными в настоящее время позиционными системами счисления являются: десятичная и двоичная Система счисления Основание Алфавит цифр Десятичная 10 0,1,2,3,4,5,6,7,8,9 Двоичная 2 0,1

Десятичная система счисления Индийская нумерация пришла сначала в арабские страны, а потом в Западную Европу. Простые и удобные правила сложения и вычитания очень больших чисел, записанной в этой системе, сделали ее особенно популярной. Эти правила вывел азиатский математик аль-Хорезми. А поскольку его труд был написан на арабском языке, то и Индийская нумерация в Европе закрепилась неправильным названием "арабское". Цифры 1,2,3,4,5,6,7,8,9,0 сложились в Индии. Древнейшая запись обнаружена в Индии и датируется 595г. Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 – углов нет, 2 – два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.

Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Позиционная система счисления Система счисления называется позиционной, если количественный эквивалент цифры в числе зависит от её положения в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.

Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причём значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания. Число в позиционных системах счисления записывается в виде суммы степеней основания (в данном случае 10), коэффициентами при этом являются цифры данного числа. 555 1,1,1,1,1 10,10,10,10,10 100,100,100,100,100 Свернутая форма записи числа 55510=5*102 +5*101 +5*100 555 Развернутая форма записи числа Позиционные системы счисления

Двоичная система счисления Позиционная система счисления, состоящая из двух цифр: 0 и 1 с основанием 2. Значение цифры зависит дополнительно от занимаемого ею места. Число 2 считается единицей 2-го разряда и записывается так: 10 (читается: «один, нуль»). Каждая единица следующего разряда в два раза больше предыдущей, т. е. эти единицы составляют последовательность чисел 2, 4, 8, 16,..., 2n,... Используется в компьютерах из-за своей простоты. Простота выполнения операций в двоичной системе счисления связана с двумя обстоятельствами: 1 — есть сигнал, 0 — нет сигнала.

Запись чисел в двоичной системе счисления В двоичной системе основание равно 2, а алфавит состоит из двух цифр (0 и 1). В развернутой форме двоичные числа записываются в виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.      Например, развернутая запись двоичного числа 1012 будет иметь вид: 1012 = 1 * 22 + 0 * 21 + 1 * 20 2 1 0

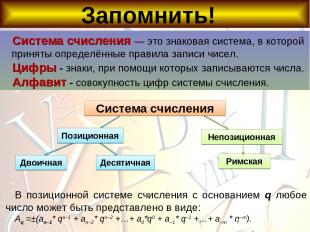
Запомнить! Непозиционная В позиционной системе счисления с основанием q любое число может быть представлено в виде: Aq =±(an–1* qn–1 + an–2* qn–2 +…+ a0*q0 + a–1* q–1 +…+ a–m * q–m). Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Цифры - знаки, при помощи которых записываются числа. Алфавит - совокупность цифр системы счисления. Система счисления Двоичная Десятичная Римская Позиционная

Логическая разминка Переложите одну палочку, чтоб равенство было верным. VI – IV = XI

Вопросы для закрепления: Система счисления это… Какие системы счисления вы знаете? Назовите основное отличие позиционных систем счисления от непозиционных? Назовите наименьшее основание для позиционной системы счисления? Какие две формы записи чисел вы знаете? Чему в десятичной системе счисления равны следующие числа, записанные римскими цифрами: а) XI; б) LX; в) MDX?

Задания для самостоятельного выполнения: Какой числовой эквивалент имеет цифра 3 в числах: 3789 3650 13 39 2. Какие числа записаны римскими цифрами: а). MCMXCIX; б). CMLXXXVIII; в). MCXLVII. 3. Некоторые римские цифры легко изобразить, используя палочки или спички. Ниже написано несколько неверных равенств. Как можно получить из них верные равенства, если разрешается переложить с одного места на другое только одну спичку (палочку)? VII - V=XI IX-V=VI VI - IX=III VIII - III=X

4. Запишите в развернутой форме числа: а) А 10=13521; г) А 10=163, 41; б) А 2=100111; в) А 2=1001,11 5. Запишите в свернутой форме следующие числа: а) А 10= 9·10 1 +1·10 0 +3·10 -1 +3·10 -2; б) А 10=10·10 2 +1·10 1 +4·10 0 +5·10 -1 в) А 2 =1 • 24 + 0 • 23 + 0 • 22 + 1 • 21 + 0 • 20 6. Какое минимальное основание имеет система счисления, если в ней записаны числа 127, 212, 101? Задания для самостоятельного выполнения:

Домашнее задание § 2,6 стр. 87. Вопросы и задания к параграфу. Подготовить сообщение о системах счисления в программе PowerPoint.

http://school-collection.edu.ru/catalog/res/402b749c-240b-4e16-9e4d-bea3fc4fa8fa/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 – История развития систем счисления http://school-collection.edu.ru/catalog/res/a96df437-5ae3-4cab-8c5f-8d4cd78c5775/?from=a30a9550-6a62-11da-8cd6-0800200c9a66&interface=catalog&class=51&subject=19&rub_guid[]=a30a9550-6a62-11da-8cd6-0800200c9a66 - Развернутая форма записи числа http://go.mail.ru/ https://ru.wikipedia.org http://inf1.info/scalenotation