Презентация на тему: Представление числовой информации

Представление числовой информации с помощью систем счисления

Цели урока: Усвоить определение следующих понятий: Система счисления, цифра, число, основание системы счисления, разряд, алфавит, непозиционная система счисления, позиционная система счисления, единичная (унарная) система счисления. Научиться записывать: десятичное число в римской системе счисления, любое число в позиционной системе счисления в развернутой форме Уметь: определять основание системы счисления приводить примеры чисел различных позиционных систем счисления объяснить разницу между числом и цифрой позиционной и непозиционной системой счисления

Говорили древнегреческие философы, ученики Пифагора, подчеркивая важную роль чисел в практической деятельности

Система счисления

системы счисления

Непозиционной называют систему счисления, в которой количественное значение цифры не зависит от ее положения в числе.

Примерами непозиционных систем счисления являются:

Единичная система счисления В древние времена, когда люди начали считать, появилась потребность в записи чисел. Первоначально количество предметов отображали равным количеством каких-нибудь значков: насечек, черточек, точек.

Десятичная древнеегипетская система счисления Для обозначения ключевых чисел использовали специальные значки-иероглифы:

Алфавитная система записи чисел До конца XVII века на Руси в качестве цифр использовались следующие буквы кириллицы, если над ними ставился специальный знак - титло. Например:

Римская система счисления До нас дошла римская система записи чисел Применяется более 2500 лет. В качестве цифр в ней используются латинские буквы: I V X L C D M 1 5 10 50 100 500 1000 Например: CXXVIII = 100 +10 +10 +5 +1 +1 +1=128

Позиционные системы счисления

Вавилонская система счисления

Позиционные системы счисления Наиболее распространенными в настоящее время являются -десятичная -двоичная -восьмеричная -шестнадцатеричная позиционные системы счисления.

Десятичная система счисления Любое число мы можем записать при помощи десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Именно поэтому наша современная система счисления называется десятичной. Известный русский математик Н.Н.Лузин так выразился по этому поводу: «Преимущества десятичной системы счисления не математические, а зоологические. Если бы у нас было на руках не десять пальцев, а восемь, то человечество бы пользовалось восьмеричной системой счисления.»

Десятичная система счисления Хотя десятичную систему счисления принято называть арабской, но зародилась она в Индии, в V веке. В Европе об этой системе узнали в ХII веке из арабских научных трактатов, которые были переведены на латынь. Этим и объясняется название «Арабские цифры». Однако широкое распространение в науке и в обиходе десятичная система счисления получила только в XVI веке. Эта система позволяет легко выполнять любые арифметические вычисления, записывать числа любой величины. Распространение арабской системы дало мощный толчок развитию математики.

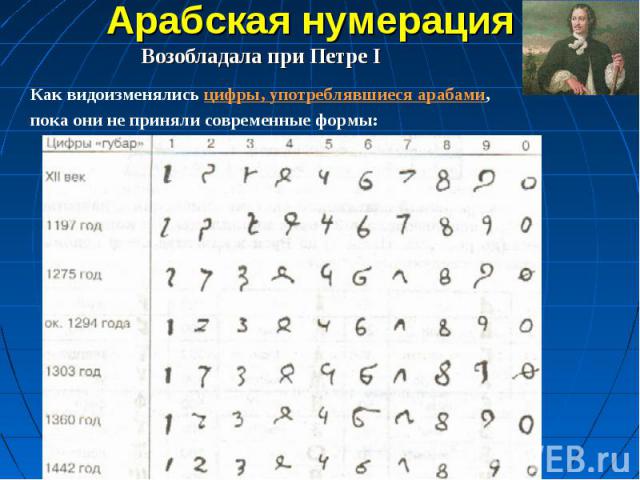
Арабская нумерация Возобладала при Петре I Как видоизменялись цифры, употреблявшиеся арабами, пока они не приняли современные формы:

Была придумана задолго до появления компьютеров. Официальное рождение двоичной арифметики связано с именем Г. В. Лейбница, опубликовавшего в 1703 г. статью, в которой он рассмотрел правила выполнения арифметических действий над двоичными числами. Ее недостаток – «длинная» запись чисел. Была придумана задолго до появления компьютеров. Официальное рождение двоичной арифметики связано с именем Г. В. Лейбница, опубликовавшего в 1703 г. статью, в которой он рассмотрел правила выполнения арифметических действий над двоичными числами. Ее недостаток – «длинная» запись чисел. В настоящий момент – наиболее употребительная в информатике, вычислительной технике и смежных отраслях система счисления. Использует две цифры: 0 и 1 Пример: Свернутая форма записи числа: 1012 2 1 0 Развернутая форма: 101 =1*22 +0*21+1*20 Все числа в компьютере представляются с помощью нулей и единиц, т. е. в двоичной системе счисления.

Позиционная система счисления Количество используемых цифр называется основанием позиционной системы счисления. За основание позиционной системы можно принять любое натуральное число больше единицы. Основание системы, к которой относится число, обозначается подстрочным индексом к этому числу. 1110010012 356418 43B8D16 Пример: основание десятичной системы счисления =10 Позиция цифры в числе называется разрядом

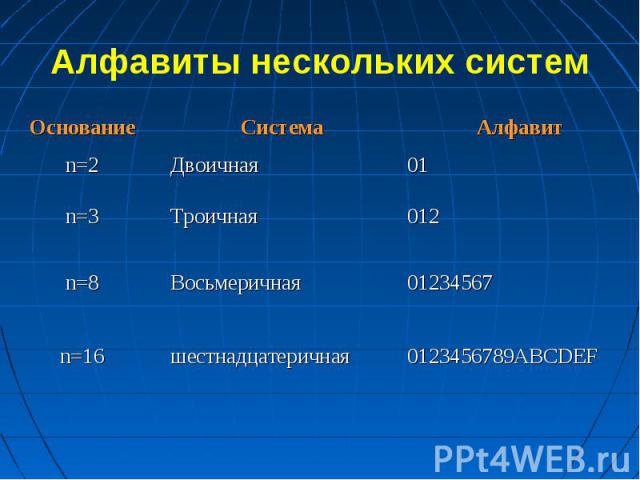
Алфавиты нескольких систем

Самостоятельная работа 1. Прочитай внимательно алгоритм выполнения заданий; 2. Выполни в тетради задание в Карточке № 1 и сдай учителю на проверку. 3. Прочитай внимательно все о римской системе счисления задание в Карточке № 2. Выполни на этом же бланке №1 и №2 обязательно, а №3 (+) если сможешь. Обменяйся с соседом по парте заданиями с бланками для взаимопроверки. 3. Прочитай внимательно все о позиционных системах счисления в Карточке № 3 и выполни на том же бланке задания: №1- заполни таблицу №2- первое задание обязательное. Со знаком(+)-дополнительно, если сможешь. Обменяйся с соседом по парте заданиями для взаимопроверки.

Карточка №1: Выписать в тетрадь основные определения понятий, заданные в явном и неявном виде: 1. Система счисления 2. Цифра 3. Число 4. Основание системы счисления 5. Разряд 6. Алфавит 7. Непозиционная система счисления 8. Позиционная система счисления 9. Единичная (унарная) система счисления

Карточка №2: Запишите в римской системе счисления числа: 1. 9 = 12 = 2778 = 2. Какие числа записаны с помощью римских цифр: LXV= MCMLXXXVI = __________________________+ (дополнительно) Исправьте неверные равенства, переложив с одного места на другое только одну палочку: VII –V = XI IX – V = VI

Карточка №3: (выполняется на этом же бланке) Задание№1: Заполни таблицу: Задание№2: Запишите в развернутой форме числа: 5,1610 = 1001,012 = __________________________+ (дополнительно) Подумай и попробуй объяснить, чем отличается позиционная система счисления от непозиционной.

Домашнее задание: §4.1.1, задания для самостоятельного выполнения: 4.1, 4.2, 4.3, 4.4, 4.5 Творческое задание: Составьте и оформите в MS Word кроссворд по теме «Системы счисления»