Презентация на тему: Дискретные модели данных в компьютере. Представление чисел

Дискретные модели данных в компьютере. Представление чисел Презентация для 10 класса

Образ компьютерной памяти

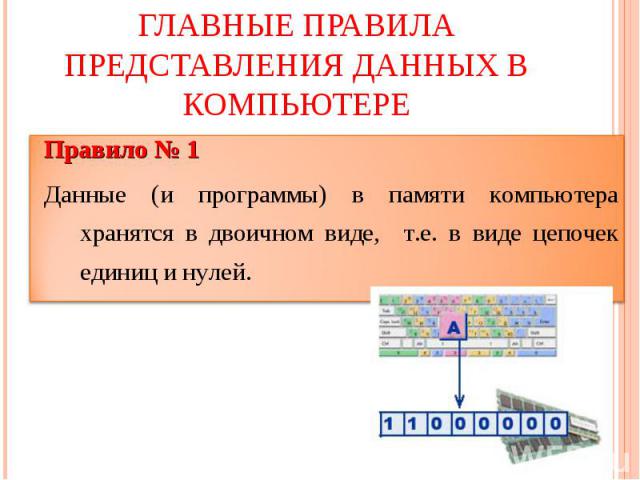
Главные правила представления данных в компьютере Правило № 1Данные (и программы) в памяти компьютера хранятся в двоичном виде, т.е. в виде цепочек единиц и нулей.

Правило № 2Представление данных в компьютер дискретно.Дискретизация — преобразование непрерывной функции в дискретную.

Дискретность (от лат. discretus — разделённый, прерывистый), прерывность; противопоставляется непрерывности. Например, дискретное изменение какой-либо величины во времени — это изменение, происходящее через определённые промежутки времени (скачками); система целых чисел (в противоположность системе действительных чисел) является дискретной . В физике и химии Д. означает зернистость строения материи, её атомистичность.ДИСКРЕТНОСТЬ [discretion] — прерывность; напр., изменение экономических показателей во времени всегда имеет прерывный характер, поскольку происходит скачками — от одной даты (года, месяца и т. д.) к другой. Понятие Д. противопоставляется понятию непрерывности.

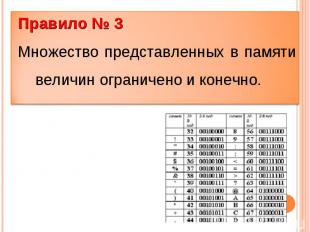
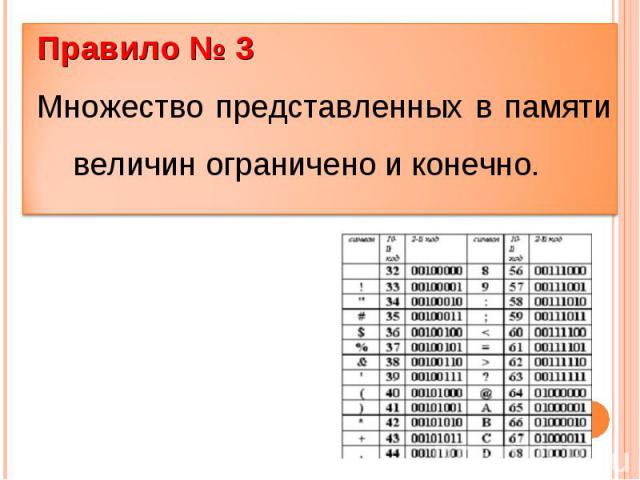
Правило № 3Множество представленных в памяти величин ограничено и конечно.

Представление чиселв ПК

Целые числа в компьютере Правило № 4В памяти компьютера числа хранятся в двоичной системе счисления.

Представление чисел в формате с фиксированной запятой Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда, т.е. вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 бит). Например, число A2 = 101010102 будет хранится в ячейке памяти следующим образом: Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках хранятся единицы. Для n-разрядного представления оно будет равно: 2n - 1

Пример. Определить диапазон чисел, которые могут хранится в оперативной памяти в формате целое неотрицательное число. Минимальное число соответствует восьми нулям, хранящимся в восьми ячейках памяти, и равно нулю. Максимальное число соответствует восьми единицам, хранящимся в ячейках памяти и равно: A = 1*27 +1*26 +1*25 + 1*24 + 1*23 + 1*22 + 1*21 + 1*20 = 1*28 – 1 = 25510 Диапазон изменения целых неотрицательных чисел от 0 до 255.

Для хранения целых чисел со знаком отводится две ячейки памяти (16 бит), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное записывается 1). Представление в компьютере положительных чисел с использованием формата «знак-величина» называется прямым кодом числа.

Например, число 200210 = 111110100102 будет представлено в 16-ти разрядном представлении следующим образом: При представлении целых чисел в n-разрядном представлении со знаком максимальное положительное число (с учетом выделения одного разряда на знак) равно: A = 2n-1 - 1

Пример. Определить максимальное положительное число, которое может хранится в оперативной памяти в формате целое число со знаком. A10 = 215 – 1 = 3276710 Для представления отрицательных чисел используется дополнительный код. Дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа A, хранящегося в n ячейках, равен 2n - A.

Дополнительный код представляет собой дополнение модуля отрицательного числа А до 0, поэтому в n-разрядной компьютерной арифметике: 2n - A + A ≡ 0 Это равенство тождественно справедливо, т.к. в компьютерной n-разрядной арифметике 2n ≡ 0. Действительно, двоичная запись такого числа состоит из одной единицы и n нулей, а в n-разрядную ячейку может уместиться только n младших разрядов, т.е. n нулей.

ПРИМЕР. ЗАПИСАТЬ ДОПОЛНИТЕЛЬНЫЙ КОД ОТРИЦАТЕЛЬНОГО ЧИСЛА –2002 ДЛЯ 16-ТИ РАЗРЯДНОГО КОМПЬЮТЕРНОГО ПРЕДСТАВЛЕНИЯ Проведем вычисления в соответствии с определением дополнительного кода: Проведем проверку с использованием десятичной системы счисления. Дополнительный код 6353410 в сумме с модулем отрицательного числа 200210 равен 6553610, т.е. дополнительный код дополняет модуль отрицательного числа до 216 (до нуля 16-ти разрядной компьютерной арифметики). Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм:

ПРАВИЛО ПОЛУЧЕНИЯ ДОПОЛНИТЕЛЬНОГО КОДА Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм: 1. Модуль числа записать прямым кодом в n двоичных разрядах; 2. Получить обратный код числа, для этого значения всех бит инвертировать (все единицы заменить на нули и все нули заменить на единицы); 3. К полученному обратному коду прибавить единицу.

ПРИМЕР ЗАПИСАТЬ ДОПОЛНИТЕЛЬНЫЙ КОД ОТРИЦАТЕЛЬНОГО ЧИСЛА –2002 ДЛЯ 16-ТИ РАЗРЯДНОГО КОМПЬЮТЕРНОГО ПРЕДСТАВЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМА. При n-разрядном представлении отрицательного числа А дополнительным кодом старший разряд выделяется для хранения знака числа (единицы). В остальных разрядах записывается положительное число: 2n-1 - A. Чтобы число было положительным должно выполняться условие: A ≤ 2n-1 Следовательно, максимальное значение модуля числа А в n-разрядном представлении равно: A = 2n-1 Тогда, минимальное отрицательное число равно: A = -2n-1

ПРИМЕР. ВЫПОЛНИТЬ АРИФМЕТИЧЕСКОЕ ДЕЙСТВИЕ 300010 - 500010 В 16-ТИ РАЗРЯДНОМ КОМПЬЮТЕРНОМ ПРЕДСТАВЛЕНИИ. Представим положительное число в прямом, а отрицательное число в дополнительном коде:

СЛОЖИМ ПРЯМОЙ КОД ПОЛОЖИТЕЛЬНОГО ЧИСЛА С ДОПОЛНИТЕЛЬНЫМ КОДОМ ОТРИЦАТЕЛЬНОГО ЧИСЛА. ПОЛУЧИМ РЕЗУЛЬТАТ В ДОПОЛНИТЕЛЬНОМ КОДЕ: Переведем полученный дополнительный код в десятичное число: 1)       Инвертируем дополнительный код: 0000011111001111 2)       Прибавим к полученному коду 1 и получим модуль отрицательного числа: 0000011111001111 + 0000000000000001 0000011111010000

3) Переведем в десятичное число и припишем знак отрицательного числа: -2000. Недостатком представления чисел в формате с фиксированной запятой является конечный диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые, так и очень большие числа.

Вывод:Целые числа в памяти компьютера – это дискретное, ограниченное и конечное множество.Границы множества целых чисел зависят от размера выделяемой ячейки памяти под целое число, а также от формата: со знаком или без знака.

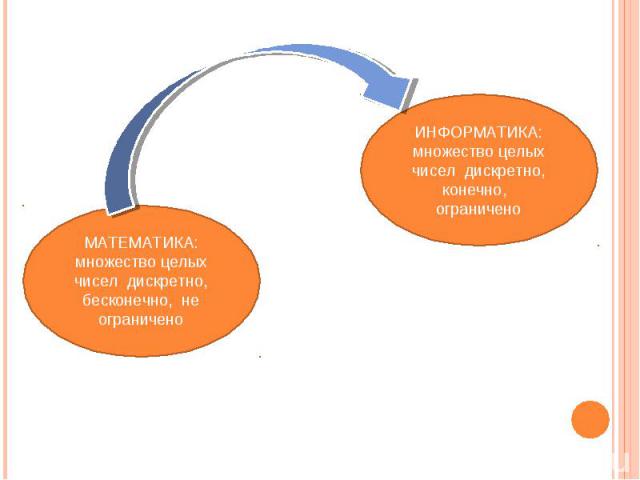
МАТЕМАТИКА:множество целых чисел дискретно, бесконечно, не ограничено ИНФОРМАТИКА:множество целых чисел дискретно, конечно, ограничено

Границы множества целых чисел зависят от размера выделяемой ячейки памяти под целое число, а также от формата: со знаком или без знака.