Презентация на тему: интерактив плакат

Приращение функции и аргумента х = х – хо – приращение аргумента f(х) = f(х) – f(хо) f(х) = f (хо + х ) – f(хо) приращение функции – Найдите f, если f(х) = х2, хо = 1, ∆х = 0,5 Решение: f(хо) = f(1) = 12 = 1, f (хо + х ) = f(1 + 0,5) = f(1,5) = 1,52 = 2,25, f = 2,25 – 1 = 1,25. Ответ: f = 1,25 изменение

Определение производной f ′(xо) – число Алгоритм: 1) ∆х, хо; 2) ∆f = f (хо + х ) – f(хо); 3) при ∆х → 0. ∆f ∆x

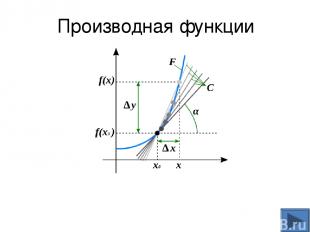
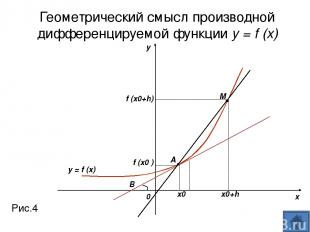
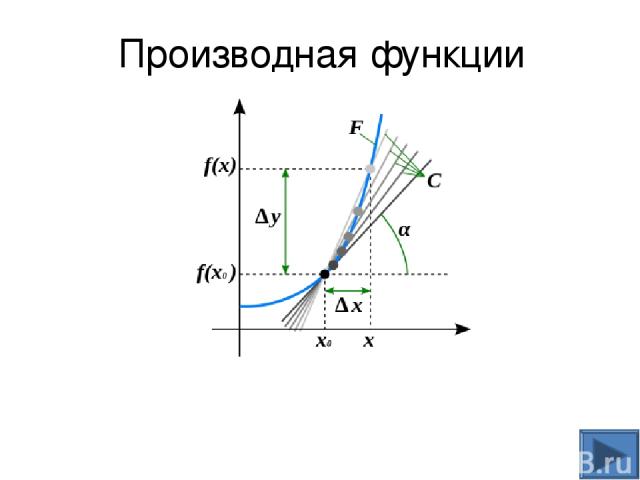
Геометрический смысл производной дифференцируемой функции y = f (x): Значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке.

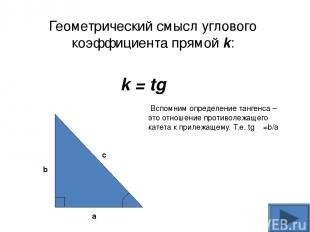
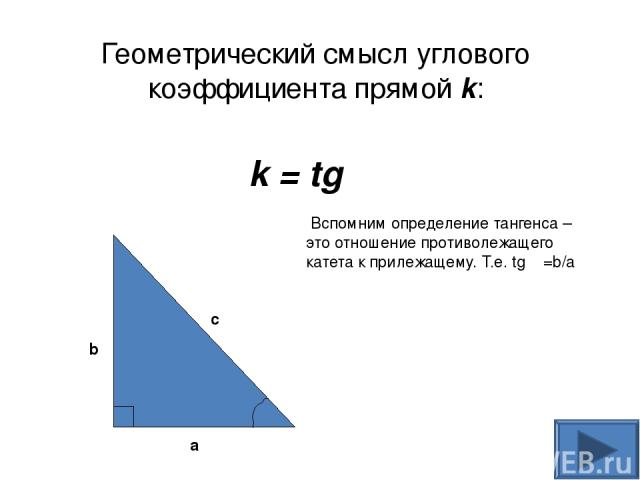
Геометрический смысл углового коэффициента прямой k: k = tg α a b c Вспомним определение тангенса – это отношение противолежащего катета к прилежащему. Т.е. tg α =b/a α

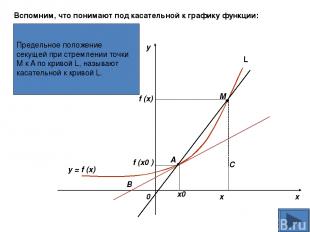
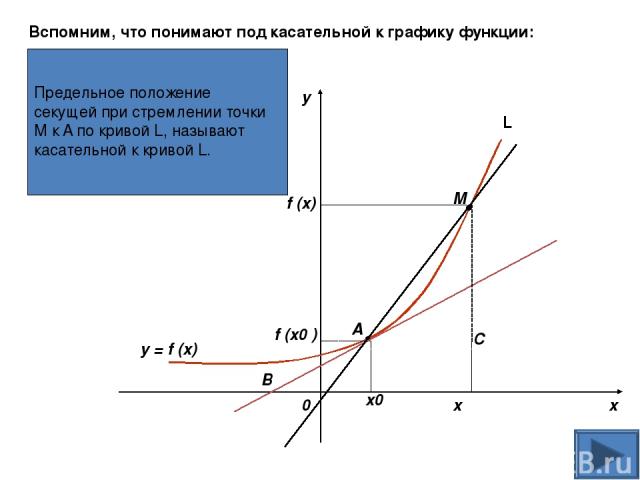
Предельное положение секущей при стремлении точки M к A по кривой L, называют касательной к кривой L. y x 0 x0 x f (x0 ) f (x) M A B C y = f (x) Вспомним, что понимают под касательной к графику функции: L

y x 0 Рис.4 y = f (x) x0 x0+h f (x0 ) f (x0+h) M A α B Геометрический смысл производной дифференцируемой функции y = f (x)

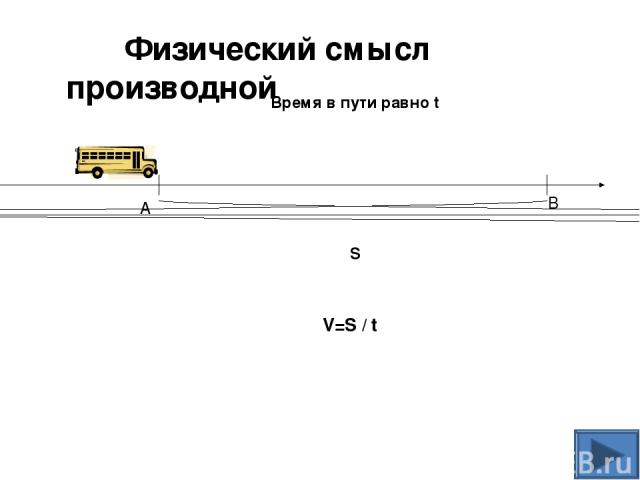
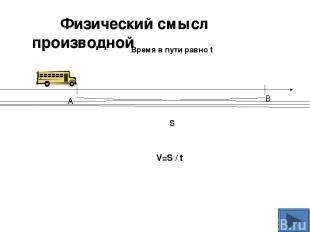
S Время в пути равно t А B V=S / t Физический смысл производной

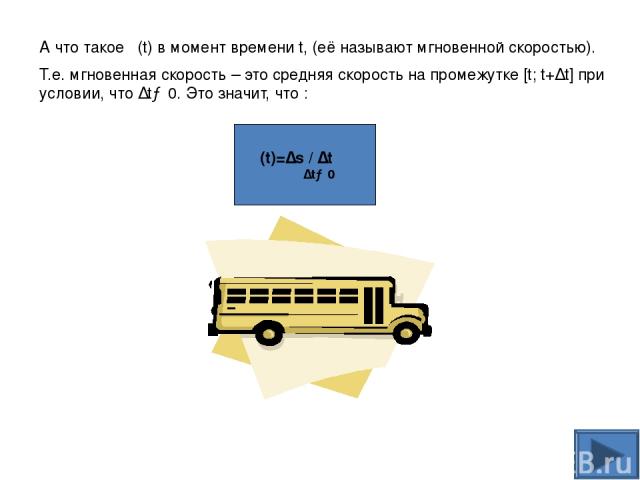
А что такое ʋ(t) в момент времени t, (её называют мгновенной скоростью). Т.е. мгновенная скорость – это средняя скорость на промежутке [t; t+∆t] при условии, что ∆t→0. Это значит, что : ʋ(t)=∆s / ∆t ∆t→0

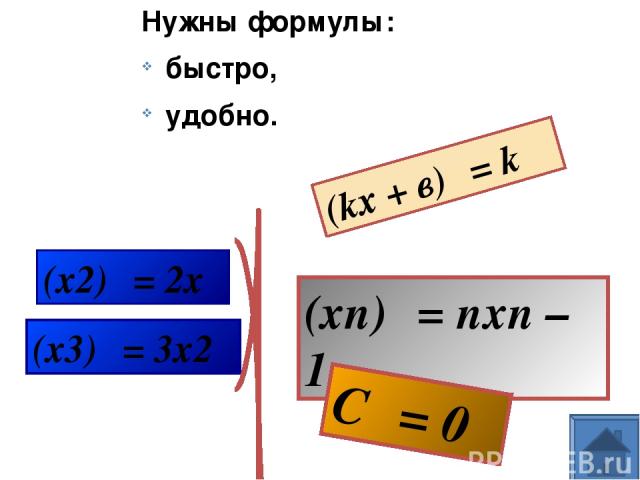
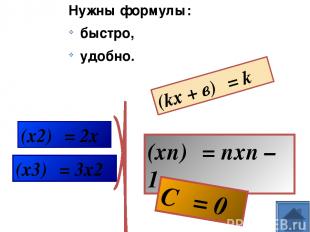
Нужны формулы: быстро, удобно. (kх + в)′ = k (х2)′ = 2х (х3)′ = 3х2 (xn)′ = nxn – 1 C ′= 0

Исаак Ньютон Английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию цвета, заложил основы современной физической оптики, создал многие другие математические и физические теории.

Готфрид Вильгельм Лейбниц Немецкий философ, логик, математик, механик, физик, юрист, историк, дипломат, изобретатель и языковед. Основатель и первый президент Берлинской Академии наук, иностранный член Французской Академии 

Спор между Лейбницем и Ньютоном В 1708 году вспыхнул печально известный спор Лейбница с Ньютоном о научном приоритете открытия дифференциального исчисления. Известно, что Лейбниц и Ньютон работали над дифференциальным исчислением параллельно и что в Лондоне Лейбниц ознакомился с некоторыми неопубликованными работами и письмами Ньютона, но пришёл к тем же результатам самостоятельно. Известно также, что Ньютон создал свою версию математического анализа, «метода флюксий»— термин Ньютона; первоначально обозначалась точкой над величиной; термин «флюксия» означает «производная»), не позднее1665 года, хотя и опубликовал свои результаты лишь много лет спустя; Лейбниц же первым сформулировал и опубликовал «исчисление бесконечно малых» и разработал символику, которая оказалась настолько удобной, что её используют и на сегодняшний день. В 1693 году, когда Ньютон, наконец, опубликовал первое краткое изложение своей версии анализа, он обменялся с Лейбницем дружескими письмами. После появления первой подробной публикации анализа Ньютона ,в журнале Лейбница «Acta eruditorum» появилась анонимная рецензия с оскорбительными намёками в адрес Ньютона; рецензия ясно указывала, что автором нового исчисления является Лейбниц, но сам Лейбниц решительно отрицал, что рецензия составлена им, однако историки нашли черновик, написанный его почерком. Ньютон проигнорировал статью Лейбница, но его ученики возмущённо ответили, после чего и разгорелась общеевропейская приоритетная война Спор между Лейбницем и Ньютоном о научном приоритете стал известен как «наиболее постыдная склока во всей истории математики». Эта распря двух гениев дорого обошлась науке: английская математическая школа вскоре увяла на целый век, а европейская проигнорировала многие выдающиеся идеи Ньютона, переоткрыв их намного позднее.