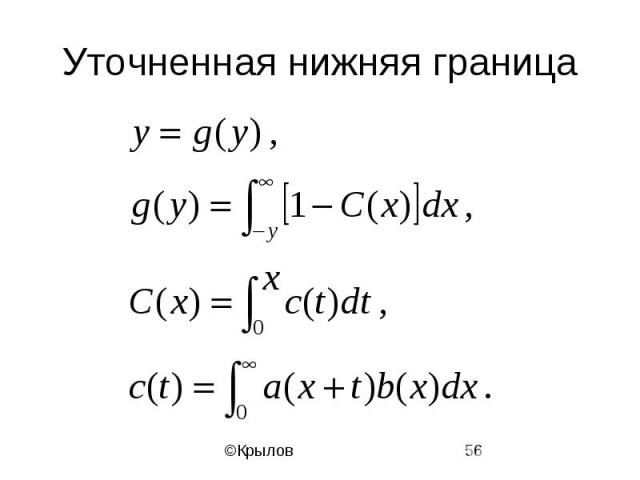Презентация на тему: Теория телетрафика

Теория телетрафика часть 2 проф. Крылов В.В.

АНАЛИТИЧЕСКИЕ МЕТОДЫ В ТЕОРИИ ТЕЛЕТРАФИКА

Вероятностная модель СМО дискретная цепь Маркова однородная цепь Маркова неприводимая цепь Маркова Возвратное и невозвратное состояние Периодическое и апериодическое возвратное состояние Возвратное нулевое и возвратное ненулевое

Цепи Маркова Теорема 1. Состояния неприводимой цепи Маркова либо все невозвратные, либо все возвратные нулевые, либо все возвратные ненулевые. В случае периодической цепи все состояния имеют один и тот же период

Цепи маркова Для неприводимой и апериодической цепи Маркова всегда существуют предельные вероятности, не зависящие от начального распределения вероятностей все состояния цепи невозвратные или все возвратные нулевые, и тогда все предельные вероятности равны нулю и стационарного состояния не существует все состояния возвратные ненулевые и тогда существует стационарное распределение вероятностей

Цепи Маркова Состояние называется эргодическим, если оно апериодично и возвратно ненулевое. Если все состояния цепи Маркова эргодичны, то вся цепь называется эргодической. Предельные вероятности эргодической цепи Маркова называют вероятностями состояния равновесия, имея в виду, что зависимость от начального распределения вероятностей полностью отсутствует.

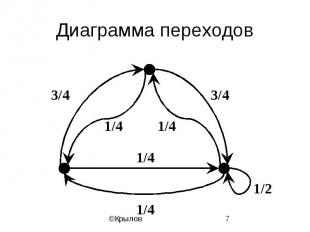
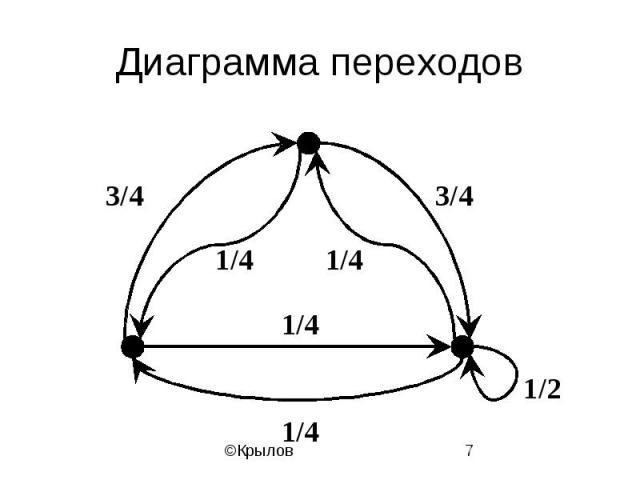
Диаграмма переходов

Решение примера

Уравнения Чепмена-Колмогорова.(Chapman - Kolmogorov)

Непрерывные цепи Маркова Случайный процесс X(t) с дискретным множеством значений образует непрерывную цепь Маркова, если Уравнение Чепмена – Колмогорова

Непрерывные цепи Маркова H(t) = [pij(t)] - матрица вероятностей перехода из состояния i в состояние j в момент времени t , а матрица Q называется матрицей интенсивностей переходов Интенсивности вероятностей переходов qij(t)

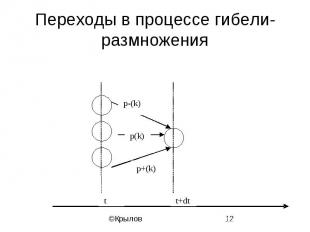
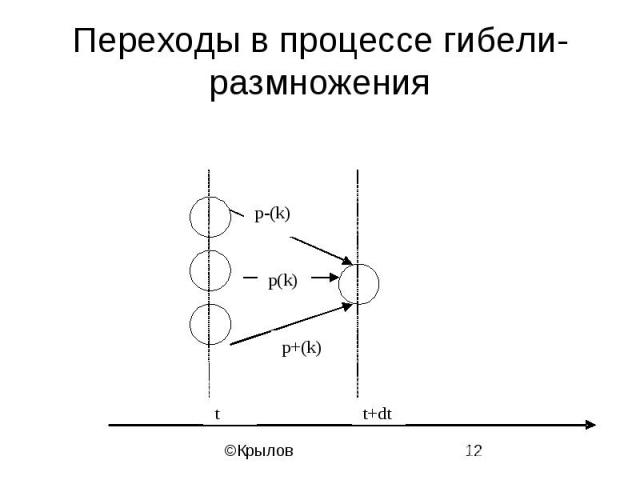
Переходы в процессе гибели-размножения

Уравнения процесса гибели-размножения

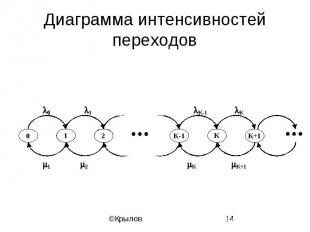
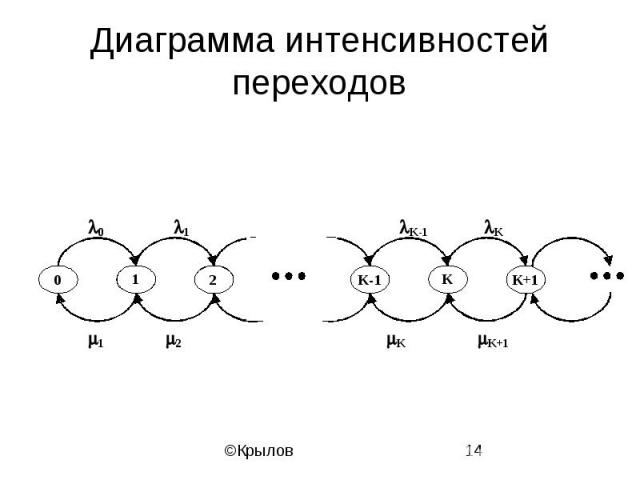
Диаграмма интенсивностей переходов

Уравнения равновесия

Решение уравнений равновесия

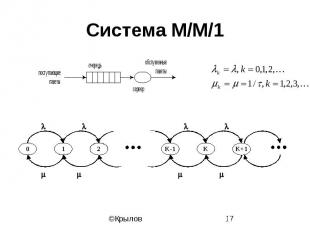
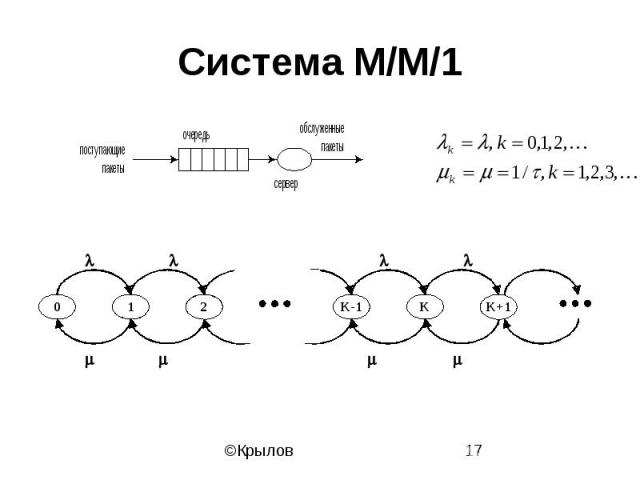
Система M/M/1

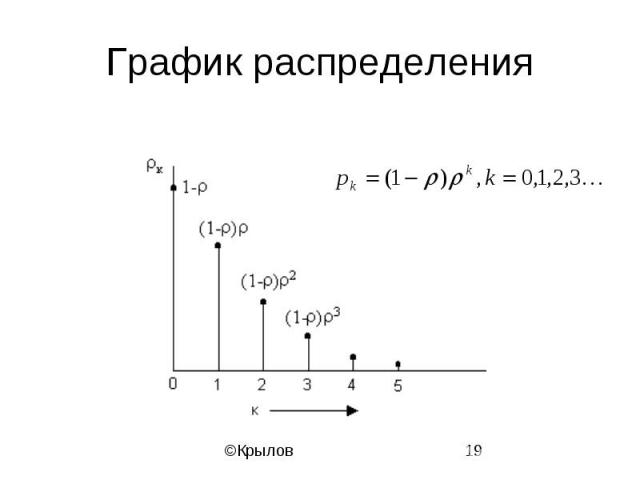
Стационарное распределение

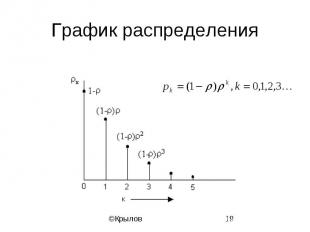
График распределения

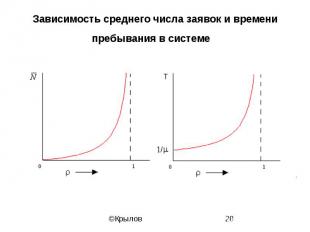
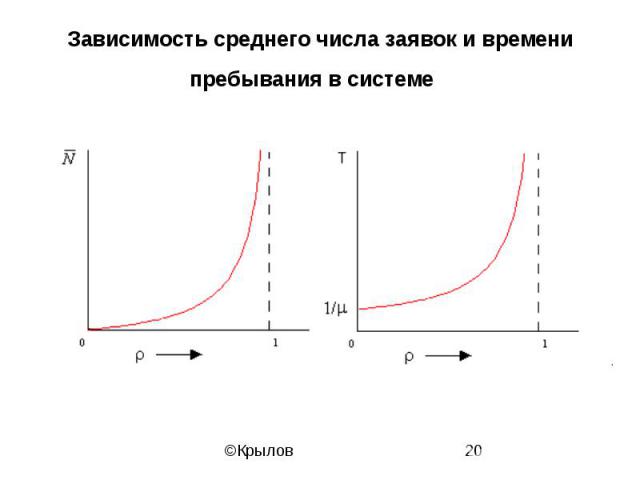
Зависимость среднего числа заявок и времени пребывания в системе

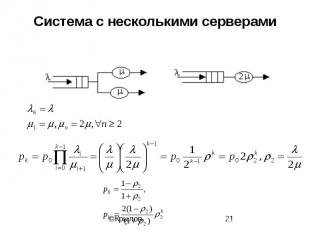
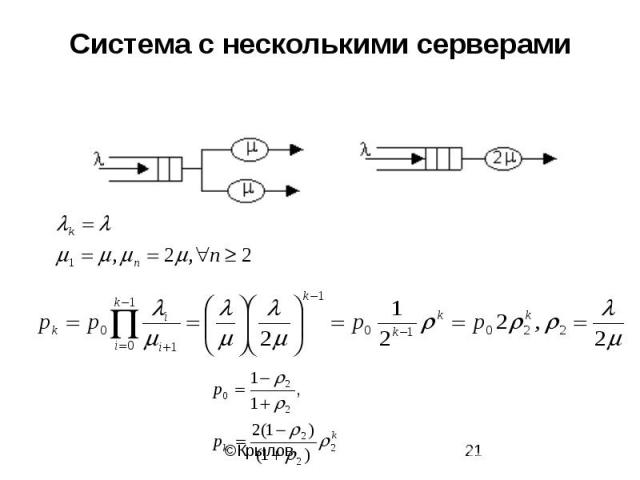
Система с несколькими серверами

Двухсерверная система

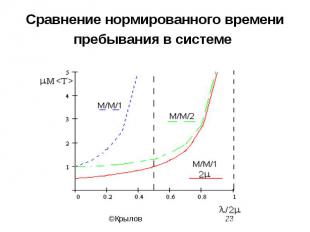
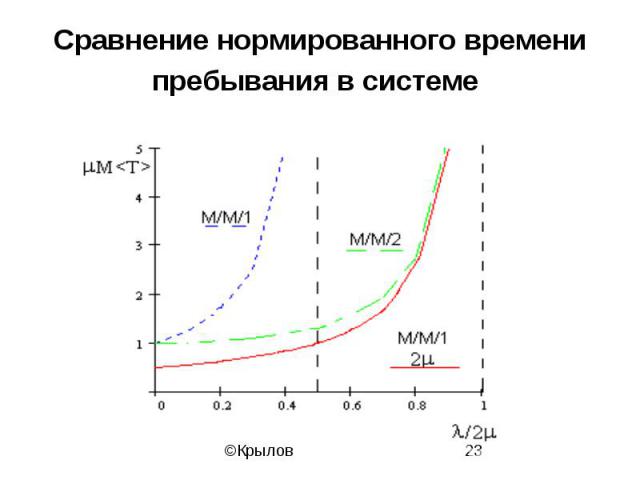
Сравнение нормированного времени пребывания в системе

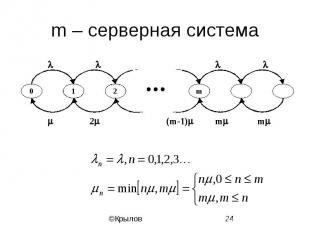
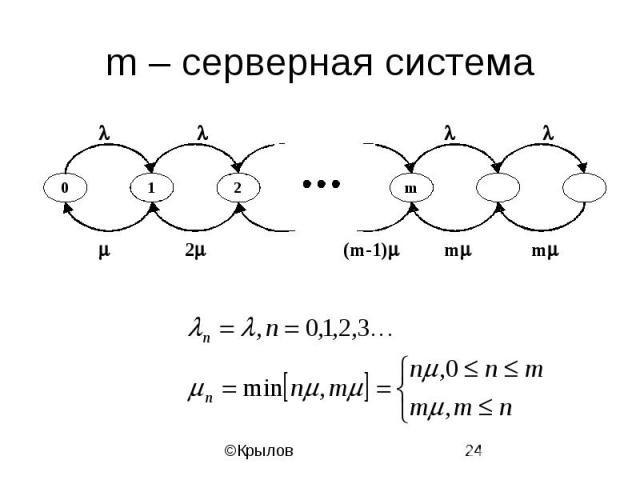
m – серверная система

m-cерверная система

С-формула Эрланга

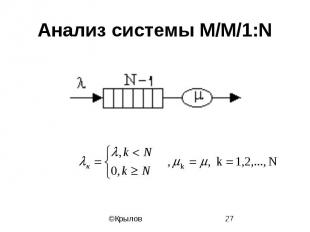
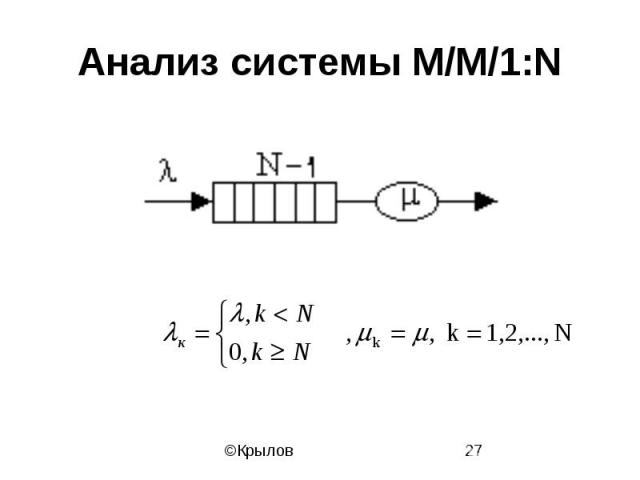
Анализ системы M/M/1:N

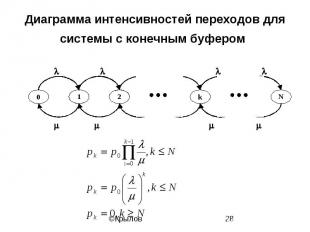
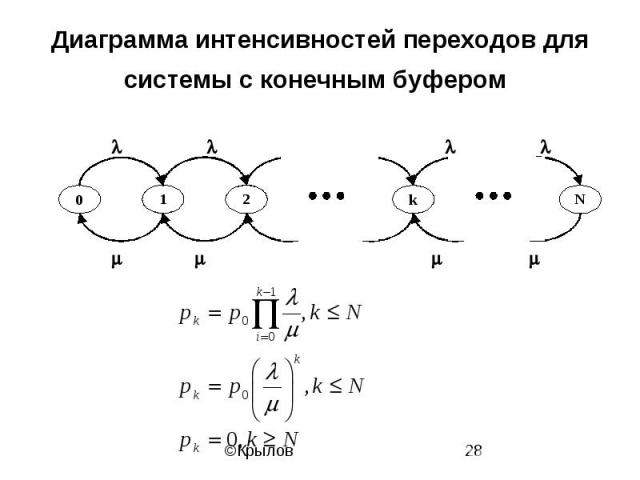
Диаграмма интенсивностей переходов для системы с конечным буфером

Стационарные вероятности

Вероятность блокировки и пропускная способность

Средняя длина очереди и задержка в системе

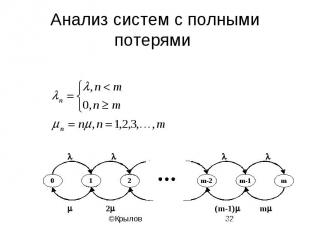
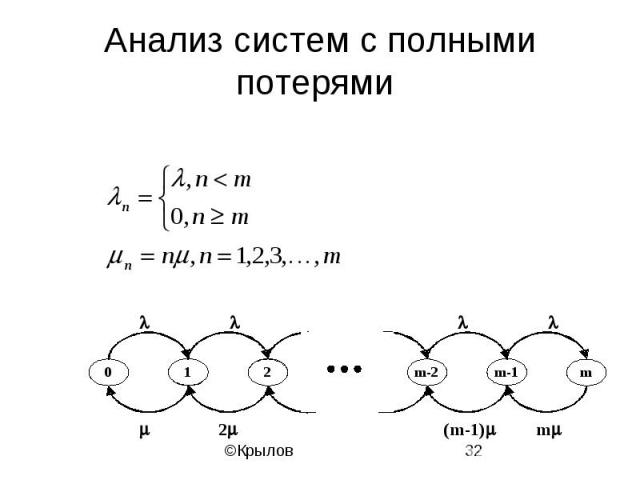
Анализ систем с полными потерями

Стационарные вероятности

В-формула Эрланга

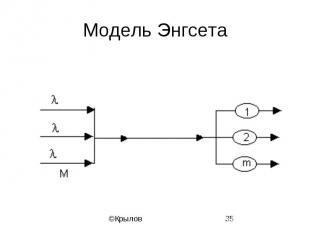
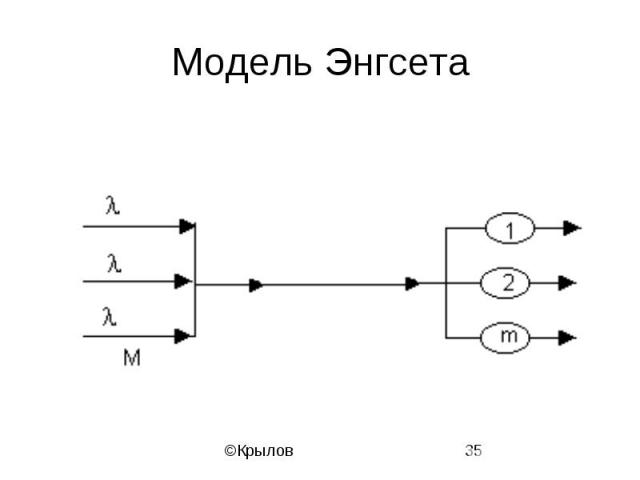
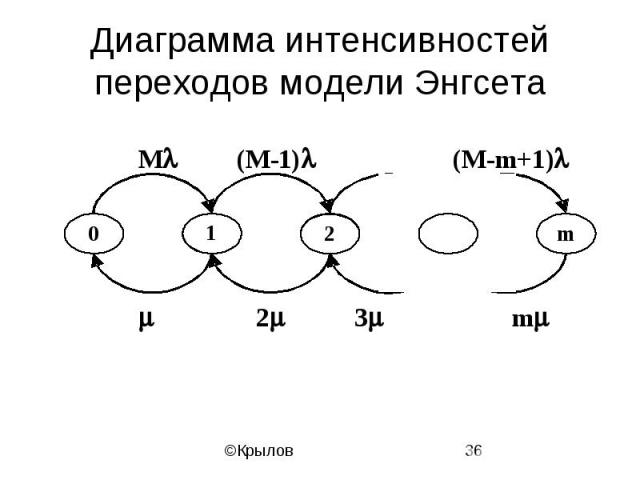
Модель Энгсета

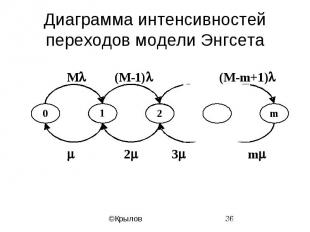
Диаграмма интенсивностей переходов модели Энгсета

Параметры и решение

Стационарные вероятности

Формула Энгсета

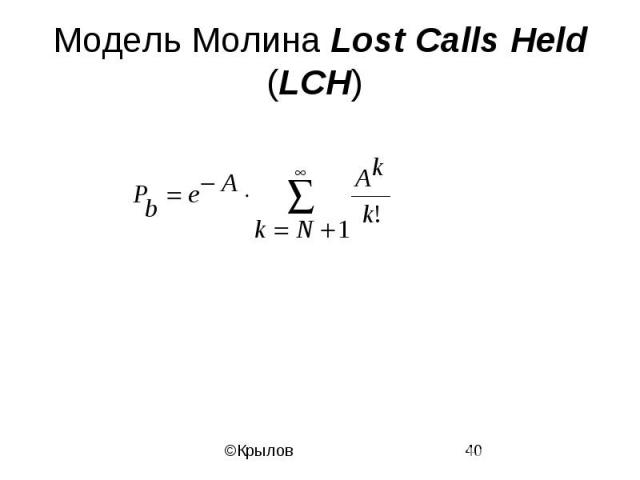
Модель Молина Lost Calls Held (LCH)

Анализ системы M/G/1

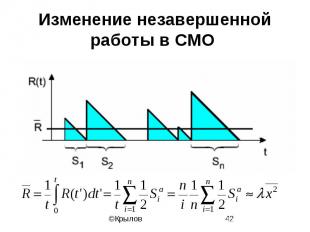
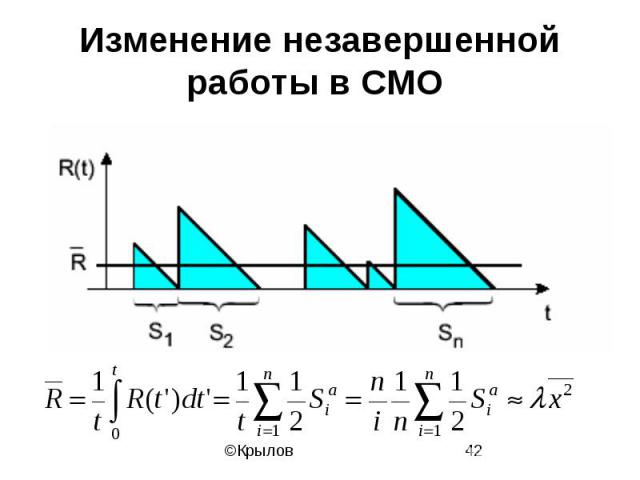
Изменение незавершенной работы в СМО

Формула Полячека-Хинчина

Среднее число требований

Система M/M/1

Система M/D/1

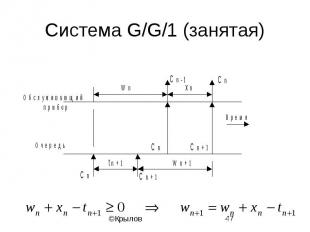
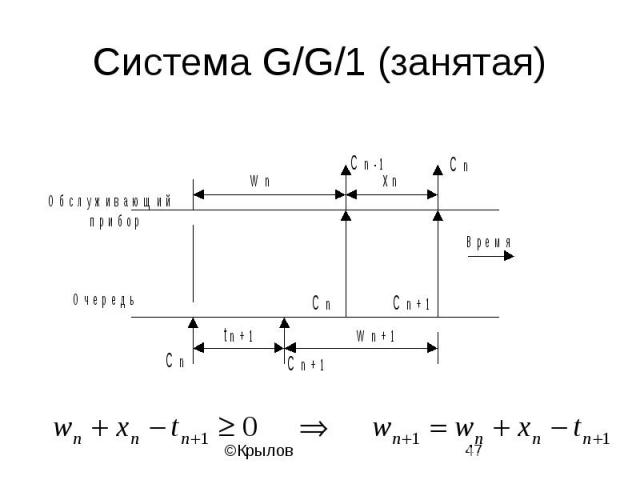
Cистема G/G/1 (занятая)

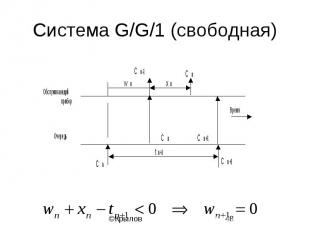
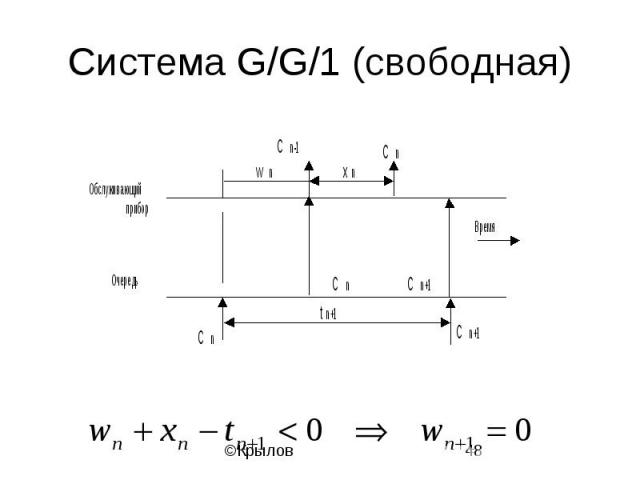
Система G/G/1 (свободная)

Связанная марковская цепь

Решение (уравнение Линдли)

Решение уравнения Линдли

Приближенное решение

Приближенное решение

Верхняя граница,граница Маршалла

Нижняя граница для потоков с монотонностью

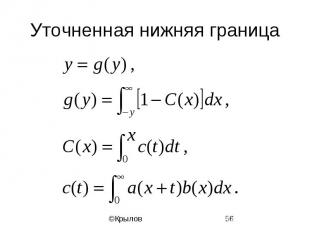
Уточненная нижняя граница

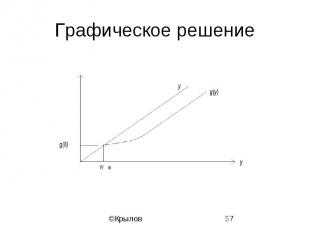
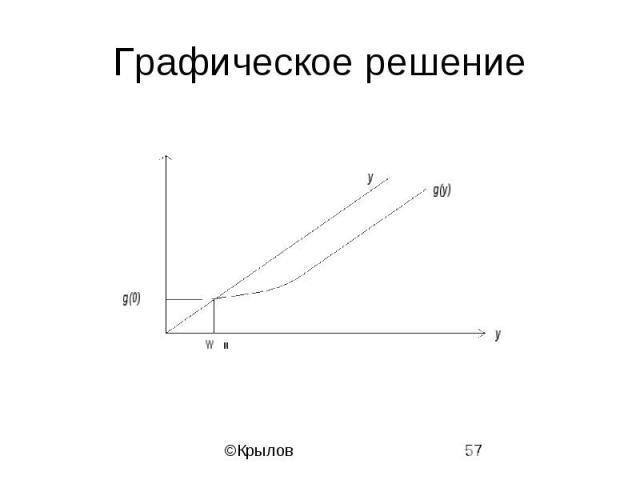
Графическое решение