Презентация на тему: ТЕХНОЛОГИИ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА

ТЕХНОЛОГИИ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА Лекция 6. Нечеткая логика

ПОНЯТИЕ НЕЧЕТКОГО МНОЖЕСТВА Основой четкого множества является характеристическая функция A

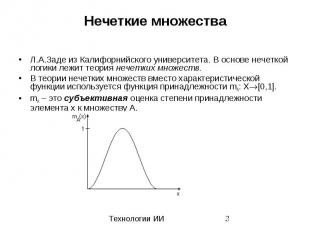
Нечеткие множества Л.А.Заде из Калифорнийского университета. В основе нечеткой логики лежит теория нечетких множеств. В теории нечетких множеств вместо характеристической функции используется функция принадлежности mA: X [0,1]. mA – это субъективная оценка степени принадлежности элемента x к множеству A.

Примеры Понятие "маленького числа" (на множестве от нуля до 10) можно определить в виде нечеткого множества A = 1/0+1/1+0.8/2+0.5/3+0.1/4+0/5+0/6+0/7+0/8+0/9+0/10 Интерпретация: число 0 однозначно является маленьким (mA=1), число 1 – тоже число 2 – уже не очень маленькое (mA=0.8). Это тем более касается чисел 3 (mA=0.5) и 4 (mA=0.1, т.е. 4 – это почти наверняка немаленькое число). числа от 5 до 10 – однозначно не маленькие (mA=0). Лингвистические переменные Не обязательно использовать числовые оценки. Зачастую, с точки зрения взаимодействия с пользователем, целесообразнее использовать т.н. "лингвистические переменные" – термины типа "много", "мало", "высокий", "низкий" и т.п.

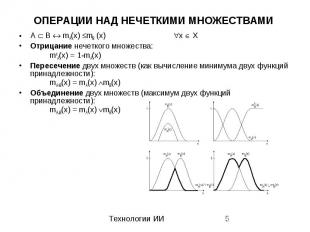
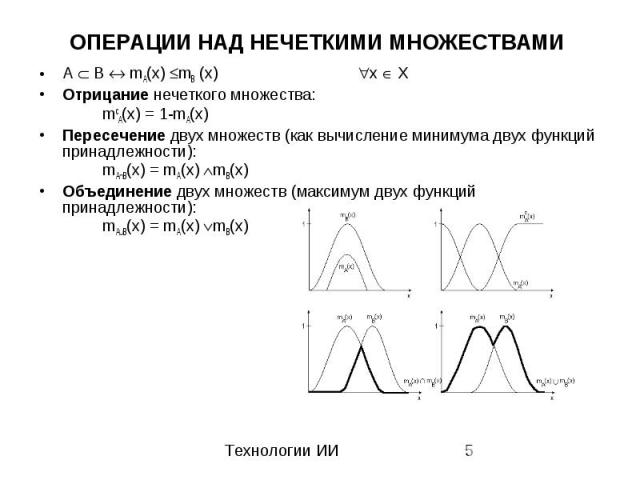
ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ A B mA(x) mB (x) x X Отрицание нечеткого множества: mcA(x) = 1-mA(x) Пересечение двух множеств (как вычисление минимума двух функций принадлежности): mA B(x) = mA(x) mB(x) Объединение двух множеств (максимум двух функций принадлежности): mA B(x) = mA(x) mB(x)

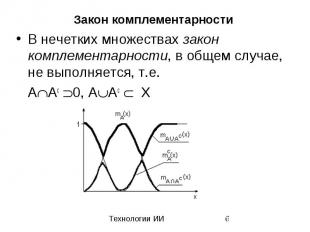
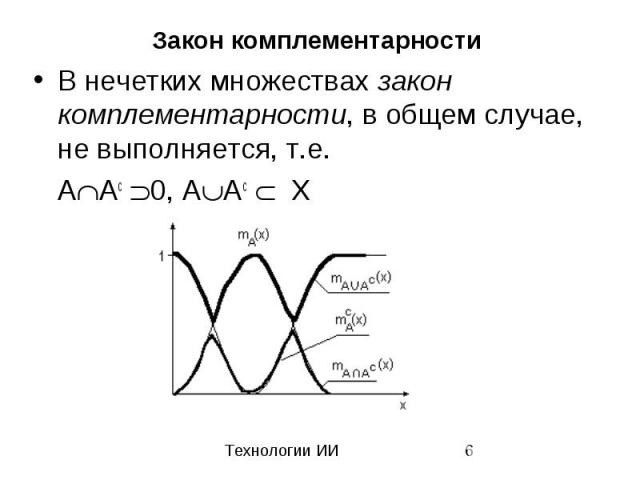
Закон комплементарности В нечетких множествах закон комплементарности, в общем случае, не выполняется, т.е. A Ac 0, A Ac X

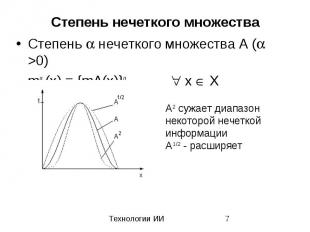
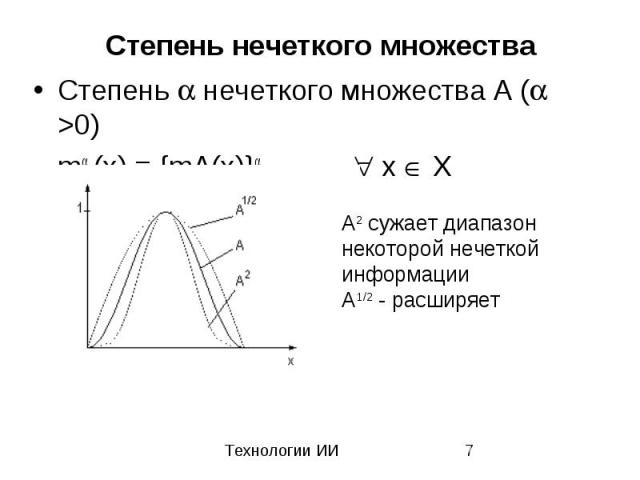
Степень нечеткого множества Степень нечеткого множества A ( >0) m A(x) = {mA(x)} x X

Прочие операции

НЕЧЕТКИЕ МНОЖЕСТВА N-ГО РОДА Для НМ первого рода функция принадлежности выглядит как отображение mA: X [0,1] (mA(x) [0,1], x X) Нечеткое множество второго рода осуществляет отображение mA: X [0,1][0,1] Т.е. используются не точные оценки в определенном интервале, а в качестве значений mA(x) принимается нечеткое множество над значениями оценки в [0,1]. Пусть принадлежность некоторой величины x к A оценивается в 0.8 ( НМ 1-го рода, (а)). Если величина именно в 0.8 вызывает у нас сомнения, то можно сказать, что наша оценка лежит в интервале от 0.7 до 0.9 (б). Однако можно сказать что сама оценка представляет собой нечеткое множество. И тогда мы будем иметь дело уже с НМ 2-го рода (в).

НЕЧЕТКАЯ ЛОГИКА От рассмотрения нечетких множеств пора переходить к нечеткой логике. Рассмотрим расширение операций НЕ, И, ИЛИ до нечетких операций, называемых нечетким отрицанием, t-нормой и s-нормой соответственно. При этом мы дадим сначала определение того, какими свойствами должна обладать операция, а затем приведем примеры возможной реализации этой операции (с точки зрения математики это красиво).

Аксиоматика определений

Аксиоматика определений

НЕЧЕТКИЕ ВЫВОДЫ И НЕЧЕТКАЯ ИМПЛИКАЦИЯ Теперь мы имеем полный набор нечетких логических операций. Осталось только понять, каким образом мы сможем применять их в процессе логического вывода. На практике нечеткая логика применима особенно тогда, тогда мы имеем дело с приближенными рассуждениями – приближенными оценками, приближенными правилами и т.п. Пусть, к примеру, существуют знания эксперта в виде

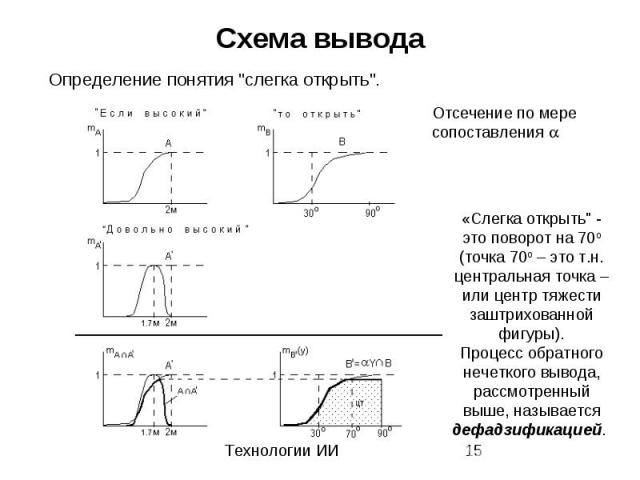
Определение понятий "Высокий" ("уровень воды высокий") : "Высокий" = 0.7/1.5м + 0.3/1.6м + 0.7/1.7м + ... + 1/2м + 1/2.1м + 1/2.2м "Открыть" ("открыть кран"): "Открыть" = 0.1/30о + 0.2/40о + ... + 0.8/70о + 1/80о + 1/90о "Уровень воды довольно высокий": "Довольно высокий" = 0.5/1.6м + 1/1.7м + 0.8/1.8м + 0.2/1.9м Итак, мы получаем следующую формальную схему:

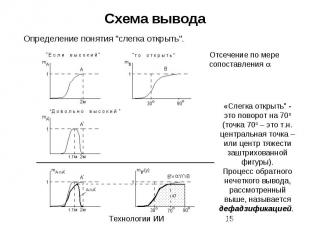
Схема вывода Определение понятия "слегка открыть".

Нечеткая импликация Основная операция логического вывода – это импликация. Обычно в качестве импликации используется t-норма типа логического произведения: x1 x2 = x1 x2 mR(x,y) = mA B(x,y) = (1-mA(x)+mB(y)) 1

Получение нечеткого результата вывода Если дано знание эксперта в виде нечеткого отношения R=A B, то процесс получения нечеткого результата вывода B' с использованием данных наблюдения A' и знания A B можно представить как B' = A'•R = A'•(A B), где ' '- т.н. композиционное правило нечеткого вывода. В частности, имеем

Пример системы нечеткого управления Нечеткое управление скоростью Задача плавного торможения/разгона поезда при соблюдении условия максимально точного позиционирования состава относительно пассажирской платформы. Нечеткие контроллеры

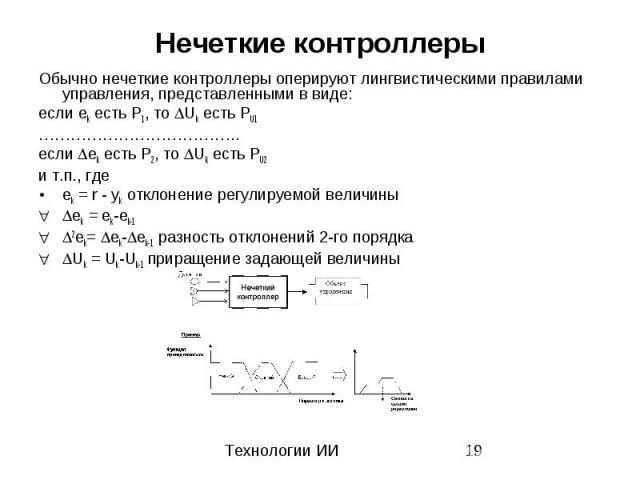
Нечеткие контроллеры Обычно нечеткие контроллеры оперируют лингвистическими правилами управления, представленными в виде: если ek есть P1, то Uk есть PU1 ……………………………….. если ek есть P2, то Uk есть PU2 и т.п., где ek = r - yk отклонение регулируемой величины ek = ek-ek-1 2ek= ek- ek-1 разность отклонений 2-го порядка Uk = Uk-Uk-1 приращение задающей величины

Нечеткие контроллеры Нечеткий контроллер содержит: блок фазификации, базу знаний, блок решений блок дефазификации. Блок фазификации преобразует четкие величины, измеренные на выходе объекта управления, в нечеткие величины, описываемые лингвистическими переменными в БЗ. Блок решений использует нечеткие условные правила, заложенные в БЗ, для преобразования нечетких входных данных в требуемые управляющие воздействия также нечеткого характера. Блок дефазификации преобразует нечеткие данные с выхода блока решений в четкую величину, которая используется для управления объектом.

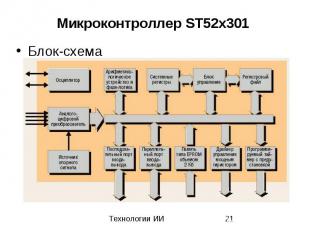
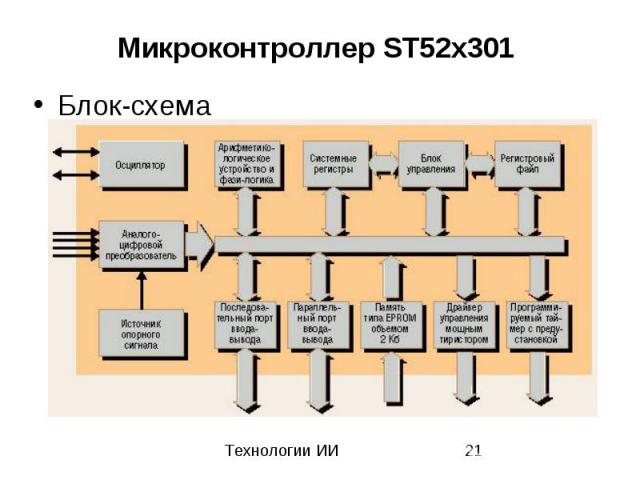
Микроконтроллер ST52x301 Блок-схема

Задача управления автомобилем Передаточная функция объекта управления (блок управления + карбюратор + автомобиль) имеет вид

Заключение Zadeh, Lotfi. Fuzzy Sets / Information and Control, 8(3), June 1965, pp.338-53. В 1989 году Национальный научный фонд США обсуждал вопрос об исключении НЛ из всех институтских учебников 1990. Комитет по контролю над экспортом (COCOM) внес НЛ в список критически важных оборонных технологий, не подлежащих экспорту потенциальному противнику. Fuji Bank. Решение сложной финансовой задачи - игра на рынке ценных бумаг в режиме “on-line”. Первый год использования новой системы приносил банку в среднем $770’000 в месяц (официально). Нечеткая ЭС, управляющая игрой “электронного трейдера”, состоит всего из 200 правил (50 из которых взяты непосредственно из классического учебника Murphy по финансовому анализу).