Презентация на тему: Независимые события. Умножение вероятностей

Презентация по теории вероятностей и статистике Ученицы Николаевой Марии 8 «А» класса На тему: «Независимые события. Умножение вероятностей».

В жизни мы часто встречаемся с ситуациями, когда события некоторым образом связаны. С наступлением одного события можно судить о вероятности другого. (На небе тучи, значит более вероятен дождь, чем солнце) Бывают события которые не связаны друг с другом. С наступлением одного из них нельзя судить о вероятности другого. (Бросание двух игральных костей). Такие события называют независимыми. Для них есть формула: Р(А В) = Р(А) * Р(В)

Определение: Событие А и В называются независимыми, если вероятность их пересечения равна произведению их вероятностей. Чаще всего о независимости событий судят не потому, выполняется или нет равенство (указано в пред идущем слайде), а по тому, как организован опыт, в котором эти события наступают.

Пример 1. Событие А – «на первой кости выпало более трёх очков». Событие В – «на второй кости выпало менее трёх очков». Будут ли события А и Б независимыми? Элементарные события, благоприятствующие событиям А, В и А В, даны в таблицах. Зная число элементарных событий, благоприятствующих каждому событию, несложно обнаружить, что Р(А) = 1, Р(В) = 1 2 3

6;6 6;5 6;4 6;3 6;2 6;1 6 5;6 5;5 5;4 5;3 5;2 5;1 5 4;6 4;5 4;4 4;3 4;2 4;1 4 3;6 3;5 3;4 3;3 3;2 3;1 3 2;6 2;5 2;4 2;3 2;2 2;1 2 1;6 1;5 1;4 1;3 1;2 1;1 1 6 5 4 3 2 1 18 элементарных событий, благоприятствующих событию А

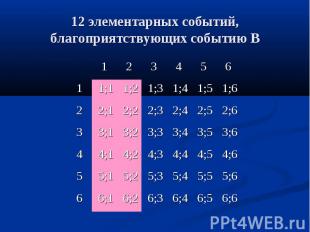
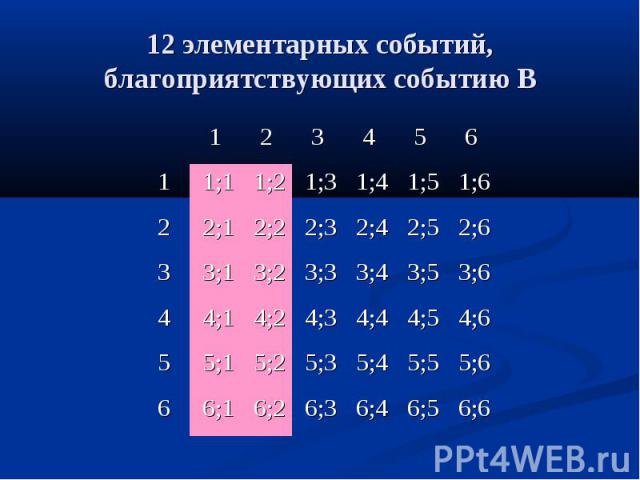
6;6 6;5 6;4 6;3 6;2 6;1 6 5;6 5;5 5;4 5;3 5;2 5;1 5 4;6 4;5 4;4 4;3 4;2 4;1 4 3;6 3;5 3;4 3;3 3;2 3;1 3 2;6 2;5 2;4 2;3 2;2 2;1 2 1;6 1;5 1;4 1;3 1;2 1;1 1 6 5 4 3 2 1 12 элементарных событий, благоприятствующих событию В

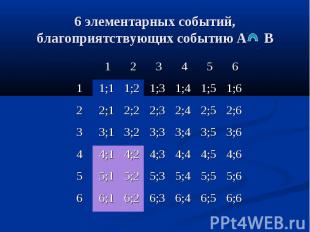
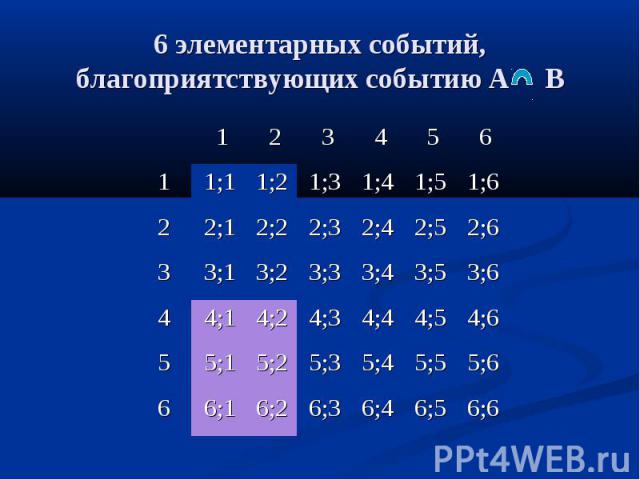
6;6 6;5 6;4 6;3 6;2 6;1 6 5;6 5;5 5;4 5;3 5;2 5;1 5 4;6 4;5 4;4 4;3 4;2 4;1 4 3;6 3;5 3;4 3;3 3;2 3;1 3 2;6 2;5 2;4 2;3 2;2 2;1 2 1;6 1;5 1;4 1;3 1;2 1;1 1 6 5 4 3 2 1 6 элементарных событий, благоприятствующих событию А В

Заметим, что Р(А) * Р(В) = 1 * 1 = 1 = Р (А В). 2 3 6 Следовательно, события А и В независимы.

ПОДВЕДЁМ ИТОГ: Мы познакомились с независимыми событиями. Мы узнали, что независимость событий часто связана с независимостью опытов, в которых они наступают.