Презентация на тему: Математические методы проверки гипотез

Математические методы проверки гипотез или «Как оценить значение полученных результатов с помощью статистики?»

Гипотеза – это… Гипотеза исследования Теоретическая: объясняет причины и внутренние закономерностей эмпирически исследуемых явлений Эмпирическая: носит описательный характер, т.е. содержит предположение о том, как ведет себя объект, но не объясняет почему

Теория статистического вывода Это формализованная система методов решения задач переноса выводов, полученных у исследуемой выборки, на генеральную совокупность.

Статистическая гипотеза Ответ на вопрос «Могут ли наши данные говорить в пользу гипотезы исследования?»; Формальное предположение о том, что сходство (или различие) некоторых характеристик случайно или, наоборот, неслучайно.

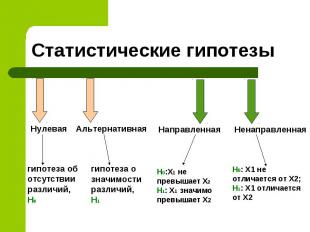
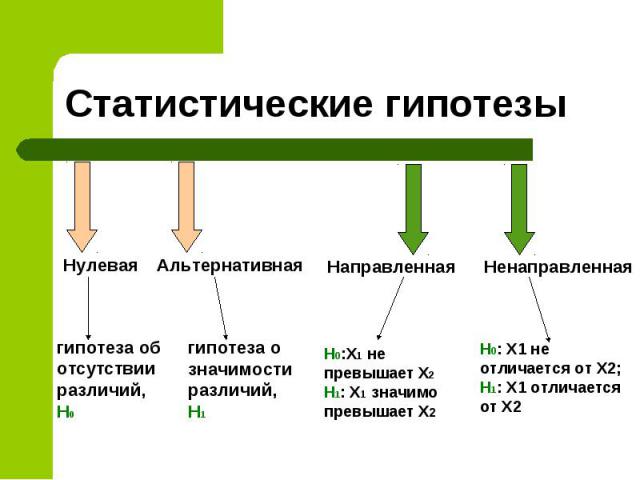
Статистические гипотезы Нулевая гипотеза об отсутствии различий, H0 Альтернативная Направленная гипотеза о значимости различий, H1 H0: X1 не отличается от Х2; Н1: Х1 отличается от Х2 Ненаправленная H0:X1 не превышает X2 H1: X1 значимо превышает Х2

Возможные исходы исследования Гипотеза: тревожность у первокурсников выше, чем у второкурсников Направленная статистическая гипотеза H1: «Показатель тревожности по группе первокурсников (Х1) будет выше, чем по группе второкурсников (Х2)» Если и правда X1>X2, отвергаем Ho, оставляем H1; Подтверждаем нашу исходную гипотезу... НО!

Возможны ошибки! Ошибка первого рода - принято решение отклонить гипотезу Н0, хотя в действительности она была верной (различия несущественны, а исследователь поднял «ложную тревогу»); Ошибка второго рода - принято решение не отклонять гипотезу Н0, хотя в действительности она была неверна (различия были значимы, а исследователь упустил возможность).

Ошибки проверки стат. гипотез Результат проверки гипотезы Но На деле: Но была верна На деле: Но была не верна Но отклонили Ошибка первого рода Верное решение Но приняли Верное решение Ошибка второго рода Мы всегда опровергаем остальные гипотезы (H0), а не доказываем свою (H1). Почему? См. принцип фальсификации

Как не допустить ошибки? Для преодоления ошибок первого рода - опираться на уровень значимости (вероятность ошибочного отклонения Ho, обозначается α=0.001, =0.01, =0.05) Для преодоления ошибок второго рода — опираться на мощность критерия (чувствительность к различиям, способность верно отклонять Ho, обозначается как 1-β)

Алгоритм принятия статистического решения Формулировка нулевой и альтернативной гипотез. Определение объема выборки N. Выбор соответствующего уровня значимости (α ≤ 0.05, желательно α=0.001 или α=0.01) Выбор статистического метода, мощного и подходящего для данного типа задачи

Алгоритм принятия статистического решения 5. Вычисление эмпирического значения статистического критерия для этой выборки 6. Поиск критических значений критерия для α = 0.05 и для α=0.01 по Таблицам 7. Графическое изображение границ значимости*, нанесение критических значений

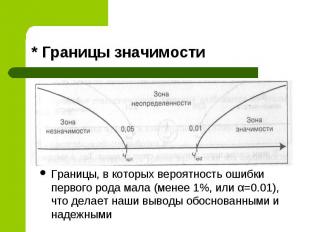
* Границы значимости Границы, в которых вероятность ошибки первого рода мала (менее 1%, или α=0.01), что делает наши выводы обоснованными и надежными

Алгоритм принятия статистического решения 8. Принятие решения о выборе гипотезы H1 или H0 9. Формулирование заключения о подтверждении/опровержении гипотезы исследования

А что такое статистические методы (или критерии)? Об этом в следующей лекции