Презентация на тему: Логика как наука. Формы мышления

Логика как наука. Формы мышления

Ученые доказали, что логическая культура не дается человеку от природы. Тогда как же она формируется? Логической культурой мышления овладевают: В ходе общения мы постепенно усваиваем правильные способы рассуждений. В школе , в вузе, изучая логику. В процессе чтения литературы.

Кому особенно полезно знать логику? Перечислите области применения логики.

Где мы с вами встретим логику?В основе логических схем и устройств ПК лежит специальный математический аппарат, использующий законы математической логики. Знание логики необходимо: при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции; при решении задач (составлении отчетов) с условиями в электронных таблицах; для построения фильтров для запросов в базах данных; для поиска информации в Интернете.

Об истории логики Термин логика происходит от древнегреческого logos, означающего «слово, мысль, понятие, рассуждение, закон». Логика - это наука о формах и способах мышления.

Аристотель (384 - 322 гг. до н.э.) Аристотель пытался найти ответ на вопрос «как мы рассуждаем». Так возникла формальная логика Рене Декарт (1596 - 1650) Рекомендовал в логике использовать общепринятые математические методы.

Готфрид Вильгельм Лейбниц (1646 - 1716 ) Предложил использовать в логике математическую символику и впервые высказал мысль о возможности применения в ней двоичной системы счисления. Так зародилась математическая, или символическая, логика.

Джордж Буль (1815 - 1864) Основоположник алгебры логики (булевой алгебры)

Большой вклад в становление и развитие математической логики внесли многие выдающиеся математики и логики XVI - XX веков, в том числе

Сперва хочу Вам в долг вменить На курсы логики ходить, Ваш ум, нетронутый доныне, На них приучат к дисциплине. Чтоб взял он направленья ось, Не разбредаясь вкривь и вкось. Гёте, «Фауст»

Область применения алгебры логикиАлгебра логики сегодня - раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.

Логика Формальная логика – это наука о законах и формах мышления. Она связана с анализом наших обычных умозаключений, выражаемых разговорным языком. Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем.

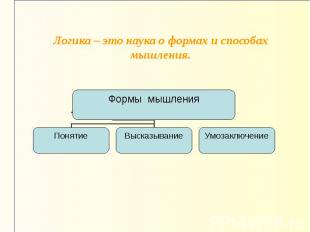
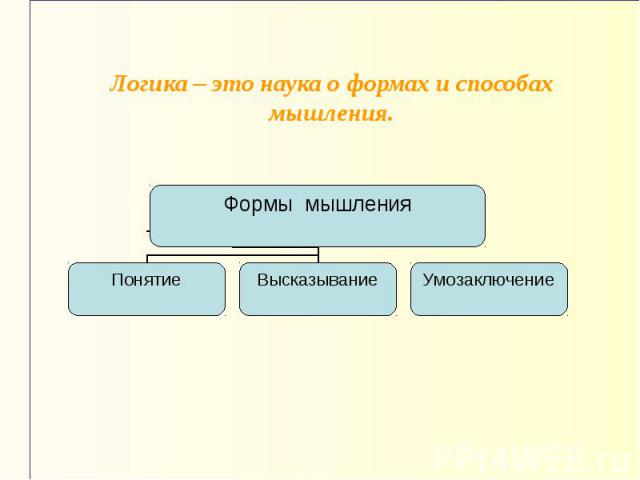
Логика – это наука о формах и способах мышления.

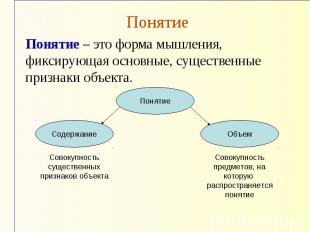
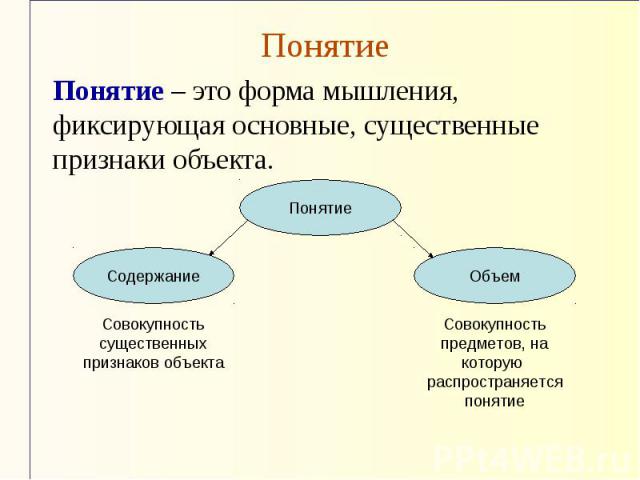
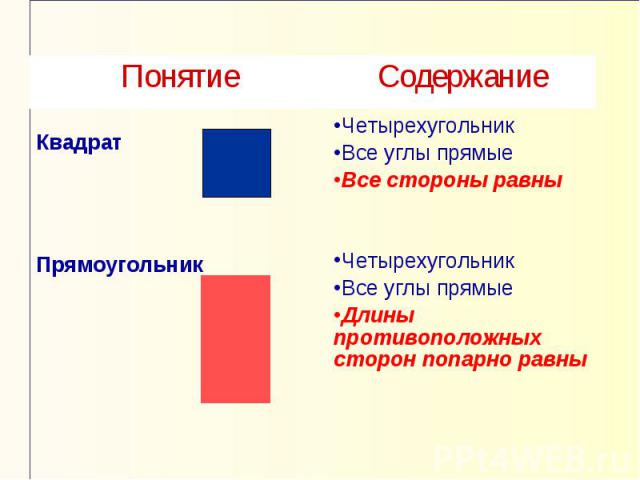
Понятие Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта.

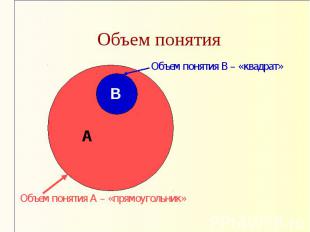
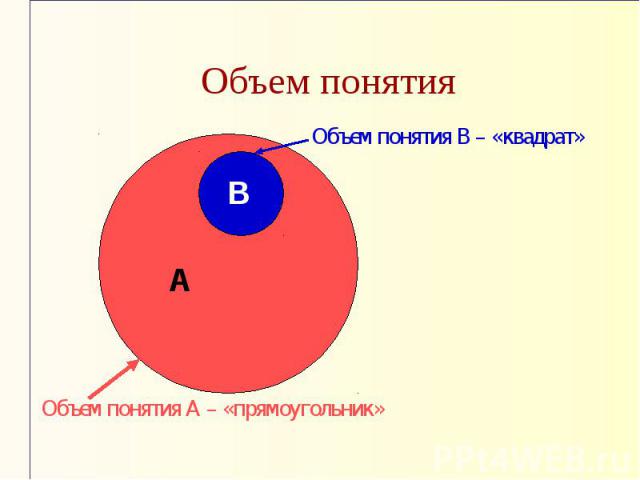
Объем понятияОбъем понятия В – «квадрат» Объем понятия А – «прямоугольник»

Несравнимые понятия Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков Примеры: Романс и кирпич Компьютер и молоко Карандаш и ледник

Эрг-упражнение для улучшения осанки "Глядя в небо" Поза: стоя В положении стоя положите руки на бедра Медленно отклоняйтесь назад, глядя на небо или в потолок. Вернитесь в исходное положение.

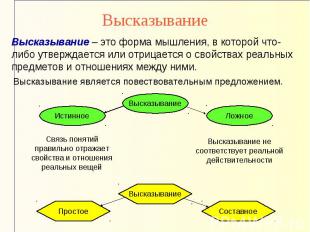
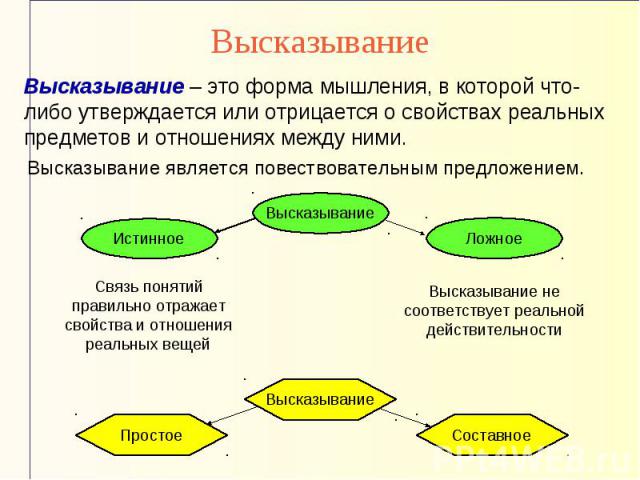
ВысказываниеВысказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание является повествовательным предложением. Связь понятий правильно отражает свойства и отношения реальных вещей Высказывание не соответствует реальной действительности

Не являются высказываниями:Предложения, о которых нельзя сказать, истинны они или ложны. Вопросительные и восклицательные предложения. Предикаты (выражения о переменных) , в которых значения переменных не определены. Он — знаменитый футболист Метеорологический прогноз. Мой друг! Отчизне посвятим души прекрасные порывы! А.С. Пушкин Любите ли Вы свой поселок? 5 +X =12 X + Z < 1 Число Y кратно 3

Виды высказываний:Частные Общие Простые Сложные выражают конкретные факты. характеризуют свойства групп объектов (явлений). не содержат в себе других высказываний. образованы из нескольких простых с помощью определенных способов соединения. . Некоторые медведи — бурые Все ученики умные Солнце светит Солнце светит и появилась радуга

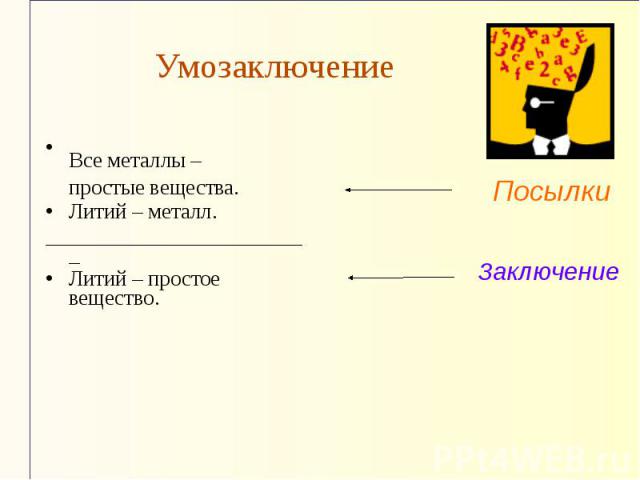
Умозаключение Умозаключение – это форма мышления, с помощью которой из одного или нескольких высказываний(посылок) может быть получено новое высказывание(вывод)

УмозаключениеВсе металлы – простые вещества. Литий – металл. _________________________ Литий – простое вещество.

Задание 1 В отрывке из поэмы А.С.Пушкина «Сказка о царе Салтане» посчитайте и назовите все понятия, а затем и все простые суждения:сколько их и какие они. Ветер по морю гуляет И кораблик подгоняет; Он бежит себе в волнах На поднятых парусах Мимо острова крутого, Мимо города большого; Пушки в пристани палят, Кораблю пристать велят.

Задание 2 Какие известные вам понятия определяются следующими предложениями: Расстояние, преодолеваемое за единицу времени. Группа слов, которая выражает законченную мысль. Часть прямой, ограниченная с двух сторон. Фигура, боковые грани которой — треугольники, а основание — многоугольник. Последовательность команд, которую выполняет компьютер в процессе обработки данных.

Задание 3 Перечислите существенные признаки, составляющие содержание следующих понятий. Каковы их объёмы? Алфавит. Палитра. Столица. Компьютер. Змей Горыныч. Груша

Задания 4 Какие из перечисленных ниже предложений являются высказываниями? Некоторые люди имеют голубые глаза. Вы были в театре? Мойте руки перед едой. Если будет дождь, то мы поедем за грибами. Завтра я сдам экзамен, либо останусь на второй год. Существую такие люди, которые не любят животных. Завтра я пойду на каток. Если я поеду туда, то смогу ли вернуться?

Задания 5 Укажите для нижеприведенных высказываний, сложные они или простые: Идет дождь. На следующем уроке будет либо контрольная работа, либо свободный урок. Завтра или сегодня брат приедет к нам в гости. Треугольники с равными сторонами не равнобедренны. От умного научишься, от глупого разучишься . Число 15 не простое. Сегодня, завтра и каждый день я буду учиться. Число 4 больше числа 2.

Задание 6. Выведите умозаключение из каждой пары посылок: Тем, кто лыс, расческа не нужна Ни одна ящерица не имеет волос Все граждане России имеют право на отдых. Я - гражданин России. Если цветы поливают, то они не засохнут. Цветы засохли. Некоторые уроки трудны. Все, что трудно, требует внимания.

4 простых высказывания.На улице идет дождь. На улице светит солнце. На улице пасмурная погода. На улице идет снег. Составьте два сложных высказывания, одно из которых всегда – ложно, а другое всегда истинно, обязательно используя все предложенные простые высказывания.

Советы для тех , кто желает совершенствовать свой ум.Недостаточно иметь хороший ум. Главное – правильно его использовать. Рене Декарт, математик и философ Побуждайте себя думать активно, а не просто держать мысли в голове. Регулярно упражняйте свой мозг. Чем больше вы упражняетесь, тем легче это дается. Действуйте.