Презентация на тему: Электронный модуль "Путешествие внутрь фрактала"

Автор: Ильин Никита Александрович Бюджетное образовательное учреждение Чувашской Республики среднего профессионального образования «Чебоксарский электромеханический колледж»


Фрактал (лат. fractus — дробленый) — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба. Масштабная инвариантность, наблюдаемая во фракталах, может быть либо точной, либо приближённой.

Термин «фрактал» введён Бенуа Мандельбротом в 1975 году. В его работах использованы результаты других учёных, работавших в той же области (Пуанкаре, Жюлиа, Кантор, Хаусдорф).

Он имеет тонкую структуру, то есть содержит произвольно малые масштабы. Он имеет некоторую форму самоподобия (по крайней мере приближённую или стохастическую). Он слишком нерегулярен, чтобы быть описанными на традиционном геометрическом языке. Он имеет дробную «фрактальную» размерность, называемую также размерностью Минковского, которая больше, чем его топологическая размерность Он имеет простое и рекурсивное определение.

В основном фракталы делят на: Геометрические; Алгебраические; Стохастические; Однако существуют и другие классификации: Рукотворные и природные. К рукотворным относятся те фракталы, которые были придуманы учёными, они при любом масштабе обладают фрактальными свойствами. На природные фракталы накладывается ограничение на область существования — то есть максимальный и минимальный размер, при которых у объекта наблюдаются фрактальные свойства.

История фракталов началась с геометрических фракталов, которые исследовались математиками в XIX веке. Фракталы этого класса — самые наглядные, потому что в них сразу видна самоподобность. Кривая Коха

В двухмерном случае такие фракталы можно получить, задав некоторую ломаную, называемую генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры (а точнее, при переходе к пределу) получается фрактальная кривая. При видимой сложности полученной кривой, её общий вид задаётся только формой генератора. Кривая дракона Кривая Пеано
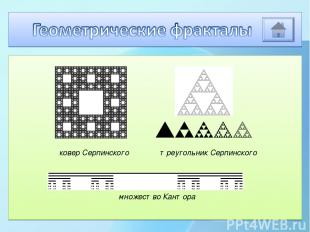
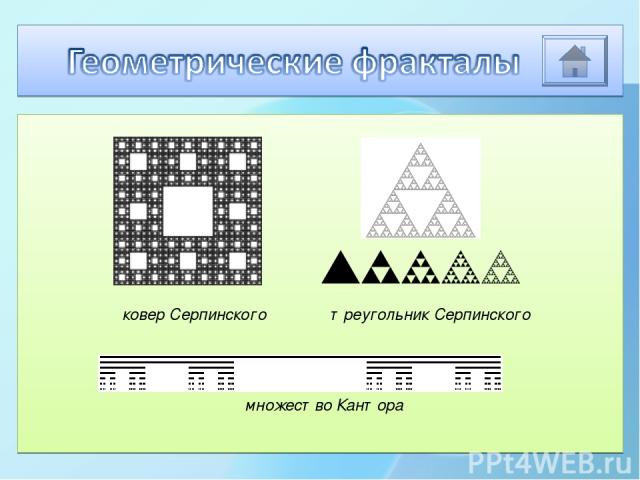
треугольник Серпинского ковер Серпинского множество Кантора

Для построения алгебраических фракталов используются итерации нелинейных отображений, задаваемых простыми алгебраическими формулами. Наиболее изучен двухмерный случай. Нелинейные динамические системы могут обладать несколькими устойчивыми состояниями. Каждое устойчивое состояние (аттрактор) обладает некоторой областью начальных состояний, при которых система обязательно в него перейдёт. Таким образом, фазовое пространство разбивается на области притяжения аттракторов. Множество Жюлиа

Алгоритм построения достаточно прост и основан на итеративном выражении: zi + 1 = F(zi), где F(z) — какая-либо функция комплексной переменной. Для всех точек прямоугольной или квадратной области на комплексной плоскости вычисляем достаточно большое количество раз zi + 1 = F(zi), каждый раз находя абсолютное значение z. При этом значения функции для разных точек комплексной плоскости могут иметь разное поведение: С течением времени | z | стремится к бесконечности; | z | стремится к 0; | z | принимает несколько фиксированных значений и не выходит за их пределы; Поведение | z | хаотично, без каких-либо тенденций.

Одним из самых распространённых способов раскрашивания точек будет сравнение |z| с заранее выбранным числом, которое считается «бесконечным», т. е. цвет точки равен номеру итерации, на которой |z| достиг «бесконечности», или чёрному в противном случае. Фрактальная форма подвида цветной капусты

Кривая Коха, как бы ни была похожа на границу берега, не может выступать в качестве её модели из-за того, что она всюду одинакова, самоподобна, слишком «правильна». Все природные объекты создаются по капризу природы, в этом процессе всегда есть случайность. Фракталы, при построении которых в итеративной системе случайным образом изменяются какие-либо параметры, называются стохастическими. К этому классу фракталов относится и фрактальная монотипия, или стохатипия. Термин «стохастичность» происходит от греческого слова, обозначающего «предположение».

Для построения плазмы необходимо использовать шаблон черно-белого изображения. Рекурсивный алгоритм для построения следующий присвоить значение оттенка для 4х углов прямоугольника. высчитать средние значения оттенков для середин сторон и центра используя среднее арифметическое. Случайно изменить центральный оттенок. Величина изменения должна зависеть от размеров прямоугольника. Разделить прямоугольник на 4 равные части, в углах которых будут полученные средние значения. Плазма

Рандомизованный фрактал строится по обычному алгоритму, за исключением того, что при вычислении на каждой итерации добавляются случайные величины. Рандомизированный фрактал на основе множества Жюлиа

Геометрические фракталы применяются для получения изображений деревьев, кустов, береговых линий и т. д. Алгебраические и стохастические — при построении ландшафтов, поверхности морей, карт раскраски, моделей биологических объектов и др. Фрактальное дерево

Фракталами хорошо описываются следующие процессы, относящиеся к механике жидкостей и газов: динамика и турбулентность сложных потоков; моделирование пламени; изучение пористых материалов, в том числе в нефтехимии.
Моделирование популяций; Биосенсорные взаимодействия; Процессы внутри организма, например, биение сердца.

Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка на зданиях внешних антенн. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, а затем присоединил к приёмнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы работы такой антенны не изучены до сих пор, это не помешало Коэну основать собственную компанию и наладить их серийный выпуск.

Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка на зданиях внешних антенн. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, а затем присоединил к приёмнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы работы такой антенны не изучены до сих пор, это не помешало Коэну основать собственную компанию и наладить их серийный выпуск.

По теореме Банаха, такие итерации всегда приводят к неподвижной точке, то есть к исходному изображению. На практике вся трудность заключается в отыскании по изображению наиболее подходящего сжимающего отображения и в компактном его хранении. Предположим что исходное изображение является неподвижной точкой некоего сжимающего отображения. Тогда можно вместо самого изображения запомнить каким-либо образом это отображение, а для восстановления достаточно многократно применить это отображение к любому стартовому изображению. Вкратце метод, предложенный Барнсли, можно описать следующим образом. Изображение кодируется несколькими простыми преобразованиями (в нашем случае аффинными), т. е. определяется коэффициентами этих преобразований (в нашем случае A, B, C, D, E, F).

Далее, поставив чёрную точку в любой точке картинки мы будем применять наши преобразования в случайном порядке некоторое (достаточно большое) число раз (этот метод ещё называют фрактальный пинг-понг). В результате точка обязательно перейдёт куда-то внутрь чёрной области на исходном изображении. Проделав такую операцию много раз мы заполним все чёрное пространство, тем самым восстановив картинку. Например, изображение кривой Коха можно закодировать четырьмя аффинными преобразованиями, мы однозначно определим его с помощью всего 24-х коэффициентов. Несмотря на то, что группой Барнсли было создано программное обеспечение, реализующее эти алгоритмы (библиотекисжатия используются в Microsoft Encarta), осталась проблема скорости сжатия. Достаточно эффективное решение не найдено до сих пор, а сам Майкл Барнсли продолжает упорно работать в выбранном направлении.

Система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.
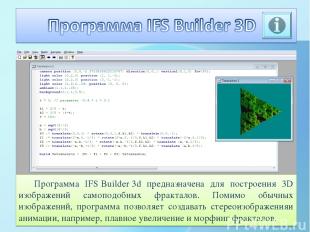
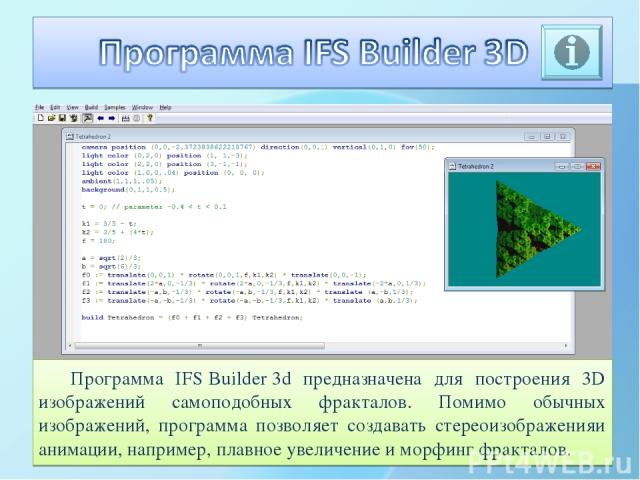
Программа IFS Builder 3d предназначена для построения 3D изображений самоподобных фракталов. Помимо обычных изображений, программа позволяет создавать стереоизображенияи анимации, например, плавное увеличение и морфинг фракталов.

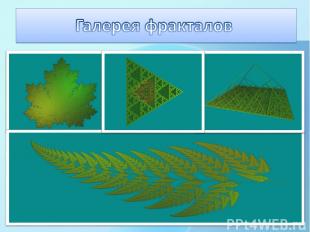
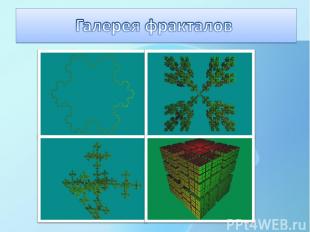
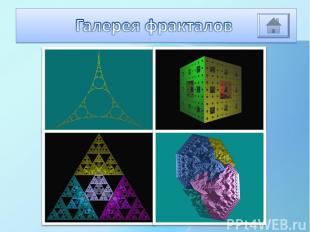

Наш первый стереофильм. Смотреть тем же методом, что и распространённые стереокартинки «третий глаз» (540x240, 30fps, 6сек).

Четыре фрактальных дерева на зеркальном квадрате. Как ни странно, квадрат попадает под определение самоподобного фрактала и порождается четырьмя подобиями.



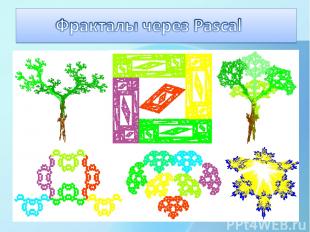


С Mind Maps нужно быть очень осторожным в том плане, что без правильного обращения они с легкостью становятся пустой тратой времени и учителя, и ученика. Если принесете на урок что-то вроде этого, и, гордый, будете ждать аплодисментов, то не дождетесь вы их. ЗАПОМНИТЬ информацию такая карта ну никак не поможет.

Одно «правильное рисование» mind map не делает их работающими Центральная идея рисуется в виде картинки не менее, чем тремя цветами, делается подпись ОДНИМ словом, далее от центральной идеи отходят ростки других «идей», причем предлагается каждый «росток» делать либо ярким, либо неярким в зависимости от того, к какой идее мы хотим привлечь внимание прежде всего
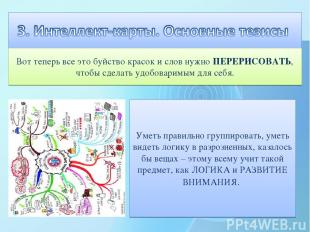
Вот теперь все это буйство красок и слов нужно ПЕРЕРИСОВАТЬ, чтобы сделать удобоваримым для себя. Уметь правильно группировать, уметь видеть логику в разрозненных, казалось бы вещах – этому всему учит такой предмет, как ЛОГИКА и РАЗВИТИЕ ВНИМАНИЯ.
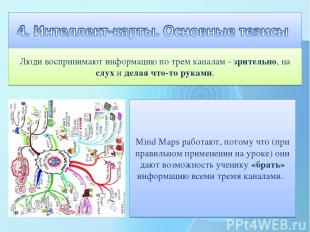
Люди воспринимают информацию по трем каналам - зрительно, на слух и делая что-то руками. Mind Maps работают, потому что (при правильном применении на уроке) они дают возможность ученику «брать» информацию всеми тремя каналами.
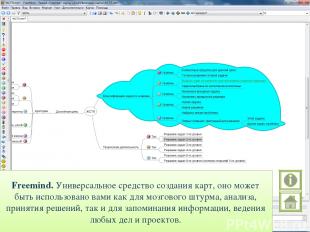
Freemind. Универсальное средство создания карт, оно может быть использовано вами как для мозгового штурма, анализа, принятия решений, так и для запоминания информации, ведения любых дел и проектов.


В методе шести шляп мышление делится на шесть различных режимов, каждый из которых представлен шляпой своего цвета.

Красная Шляпа. Эмоции. Интуиция, чувства и предчувствия. Не требуется давать обоснование чувствам. Какие у меня по этому поводу возникают чувства? Черная Шляпа. Осторожность. Суждение. Оценка. Правда ли это? Сработает ли это? В чем недостатки? Что здесь неправильно? Желтая Шляпа. Преимущества. Почему это стоит сделать? Каковы преимущества? Почему это можно сделать? Почему это сработает? Зеленая Шляпа. Творчество. Различные идеи. Новые идеи. Предложения. Каковы некоторые из возможных решений и действий? Каковы альтернативы? Белая Шляпа. Информация. Вопросы. Какой мы обладаем информацией? Какая нам нужна информация? Синяя Шляпа. Организация мышления. Мышление о мышлении. Чего мы достигли? Что нужно сделать дальше?