Презентация на тему: Зарождение и история геометрии





Муза геометрии, Лувр Муза геометрии, Лувр

Традиционно считается, что родоначальниками геометрии являются древние греки, перенявшие у египтян ремесло землемерия и измерения объёмов тел и превратившие его в науку. Превращение это произошло путём абстрагирования от всяких свойств тел, кроме взаимного положения и величины. Наукой геометрия стала, когда от набора рецептов перешли к установлению общих закономерностей. Греки составили первые систематические и доказательные труды по геометрии. Центральное место среди них занимают составленные около 300 до н. э. «Начала» Евклида. Этот труд и поныне остаётся образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом. Геометрия греков, называемая сегодня евклидовой, или элементарной, занималась изучением простейших форм: прямых, плоскостей, отрезков, правильных многоугольников и многогранников, конических сечений, а также шаров, цилиндров, призм, пирамид и конусов. Вычислялись их площади и объёмы. Преобразования в основном ограничивались подобием. Традиционно считается, что родоначальниками геометрии являются древние греки, перенявшие у египтян ремесло землемерия и измерения объёмов тел и превратившие его в науку. Превращение это произошло путём абстрагирования от всяких свойств тел, кроме взаимного положения и величины. Наукой геометрия стала, когда от набора рецептов перешли к установлению общих закономерностей. Греки составили первые систематические и доказательные труды по геометрии. Центральное место среди них занимают составленные около 300 до н. э. «Начала» Евклида. Этот труд и поныне остаётся образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом. Геометрия греков, называемая сегодня евклидовой, или элементарной, занималась изучением простейших форм: прямых, плоскостей, отрезков, правильных многоугольников и многогранников, конических сечений, а также шаров, цилиндров, призм, пирамид и конусов. Вычислялись их площади и объёмы. Преобразования в основном ограничивались подобием. Средние века немного дали геометрии, и следующим великим событием в её истории стало открытие Декартом в XVII веке координатного метода («Рассуждение о методе», 1637). Точкам сопоставляются наборы чисел, это позволяет изучать отношения между формами методами алгебры. Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями. Примерно одновременно с этим Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии. Метод координат лежит в основе появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями. Ф. Клейн связал все виды геометрий, согласно ему геометрия изучает все те свойства фигур, которые инвариантны относительно преобразований из некоторой группы. При этом каждая группа задаёт свою геометрию. Так, изометрии (движения) задаёт евклидову геометрию, группа аффинных преобразований — аффинную геометрию.

Женщина обучает детей геометрии. Иллюстрация из парижской рукописи Евклидовых «Начал», начало XIV века. Женщина обучает детей геометрии. Иллюстрация из парижской рукописи Евклидовых «Начал», начало XIV века.


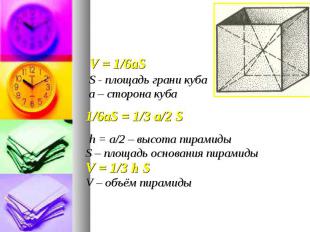
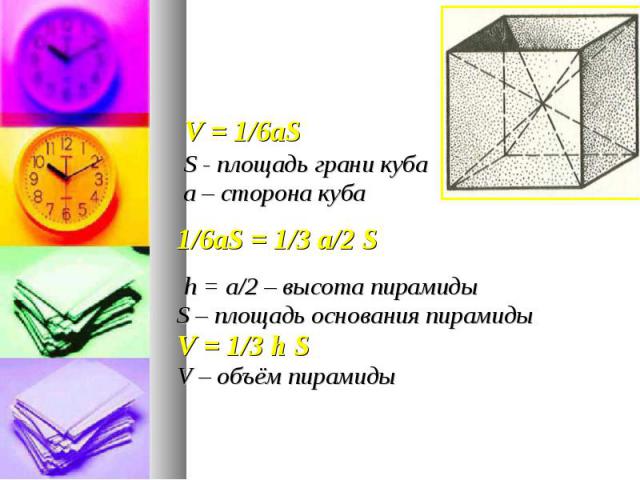
V = 1/6aS V = 1/6aS S - площадь грани куба а – сторона куба 1/6aS = 1/3 а/2 S h = а/2 – высота пирамиды S – площадь основания пирамиды V = 1/3 h S V – объём пирамиды




По–гречески скалку называли «каландер», поэтому все тела с округлым сечением получили название цилиндра. Тело, похожее на еловую шишку, которую по-гречески называли «конос», назвали конусом. Тела, напоминающие нам египетские пирамиды, так и стали называть – пирамидами. По–гречески скалку называли «каландер», поэтому все тела с округлым сечением получили название цилиндра. Тело, похожее на еловую шишку, которую по-гречески называли «конос», назвали конусом. Тела, напоминающие нам египетские пирамиды, так и стали называть – пирамидами.

Слово «параллельный» происходит от греческого «параллелос» - идти рядом. От него уже происходят слова «параллелепипед» и другие. Слово «параллельный» происходит от греческого «параллелос» - идти рядом. От него уже происходят слова «параллелепипед» и другие. Столик для еды имел две параллельные стороны и был похож на трапецию, но сначала его называли «тетрапецион», а позже уже дали истинное название – трапеция.


L=(Р1+Р2)/2 L=(Р1+Р2)/2 L – длина окружности Р1 - периметр большого квадрата Р2 - периметр малого квадрата

Самое древнее сочинение, содержащее зачатки геометрии, дошло до нас из Египта и относится примерно к 17 веку до н.э.. Геометрические сведения того периода были немногочисленны и сводились к вычислению некоторых площадей и объемов. Геометрия по свидетельству греческих историков была перенесена в Грецию из Египта в 7 веке до н.э. Здесь на протяжении нескольких поколений она складывалась в стройную систему. Самое древнее сочинение, содержащее зачатки геометрии, дошло до нас из Египта и относится примерно к 17 веку до н.э.. Геометрические сведения того периода были немногочисленны и сводились к вычислению некоторых площадей и объемов. Геометрия по свидетельству греческих историков была перенесена в Грецию из Египта в 7 веке до н.э. Здесь на протяжении нескольких поколений она складывалась в стройную систему.

http://ru.wikipedia.org/wiki/Геометрия - свободная энциклопедия. http://ru.wikipedia.org/wiki/Геометрия - свободная энциклопедия. http://www.krugosvet.ru/enc/nauka_i_tehnika/matematika/GEOMETRIYA.html