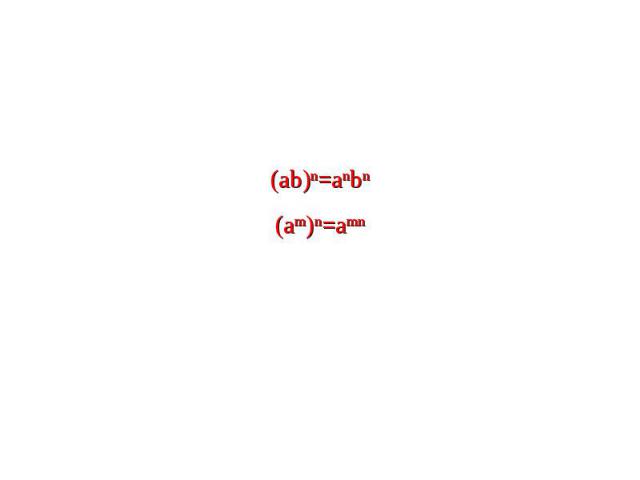Презентация на тему: Возведение одночлена в степень

Возведение одночлена в степень

=(ab)∙(ab)∙(ab)∙(ab) =(a∙a∙a∙a)∙(b∙b∙b∙b) Если a и b – произвольные числа и n – натуральное число, то:(ab)n=anbn =(ab)∙(ab)∙…∙(ab) =(a∙a∙…∙a)∙(b∙b∙…∙b)

=anbncn =anbncndn ЧТОБЫ ВОЗВЕСТИ В СТЕПЕНЬ ПРОИЗВЕДЕНИЕ, НУЖНО ВОЗВЕСТИ В ЭТУ СТЕПЕНЬ КАЖДЫЙ МНОЖИТЕЛЬ И РЕЗУЛЬТАТЫ ПЕРЕМНОЖИТЬ.

=a5∙a5∙a5∙a5 =a5+5+5+5 Если a – произвольное число, m и n – любые натуральные числа, то:(am)n=amn

ЧТОБЫ ВОЗВЕСТИ СТЕПЕНЬ В СТЕПЕНЬ, НУЖНО ОСНОВАНИЕ ОСТАВИТЬ ТЕМ ЖЕ, А ПОКАЗАТЕЛИ СТЕПЕНЕЙ ПЕРЕМНОЖИТЬ.

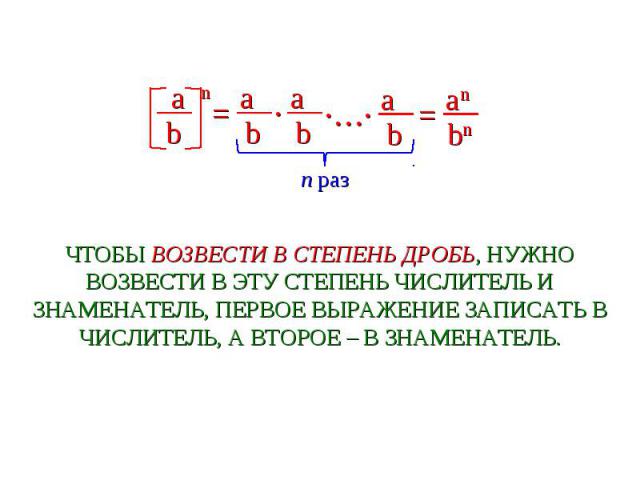
ЧТОБЫ ВОЗВЕСТИ В СТЕПЕНЬ ДРОБЬ, НУЖНО ВОЗВЕСТИ В ЭТУ СТЕПЕНЬ ЧИСЛИТЕЛЬ И ЗНАМЕНАТЕЛЬ, ПЕРВОЕ ВЫРАЖЕНИЕ ЗАПИСАТЬ В ЧИСЛИТЕЛЬ, А ВТОРОЕ – В ЗНАМЕНАТЕЛЬ.

ПРИМЕР 1: Возведем одночлен -3a3b2 в шестую степень: =(-3)6∙(a3)6∙(b2)6 (-3a3b2)6 =729a18b12

ПРИМЕР 2: Возведем одночлен –x4y3z в третью степень: (–x4y3z)3 =(-1)3∙(x4)3∙(y3)3∙z3 =-x12y9z3

(ab)n=anbn (am)n=amn