Презентация на тему: В8 по математике

Задания В8, В10 Задания В8, В10 Лосева Екатерина Анатольевна Учитель математики МОУ «Университетский лицей»

В8 Уметь выполнять действия с функциями В8 Уметь выполнять действия с функциями В10 Уметь строить и исследовать простейшие математические модели

 № 119975. Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с.  № 119975. Материальная точка движется прямолинейно по закону (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость (в м/с) в момент времени t = 9 с. Решение: Найдем закон изменения скорости: При t = 9 c имеем: Ответ: 60.

№ 323080. На рисунке изображён график некоторой функции . Функция  — одна из первообразных функции  . Найдите площадь закрашенной фигуры. № 323080. На рисунке изображён график некоторой функции . Функция  — одна из первообразных функции  . Найдите площадь закрашенной фигуры. Решение: Найдем формулу, задающую функцию график которой изображён на рисунке

№ 119974. Прямая является касательной к графику функции . Найдите с . № 119974. Прямая является касательной к графику функции . Найдите с . Решение: Условие касания графика функции и прямой задаётся системой требований

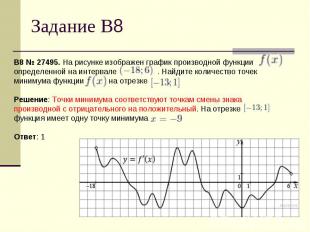
№ 323078. На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите  , где   — одна из первообразных функции   . № 323078. На рисунке изображён график некоторой функции (два луча с общей начальной точкой). Пользуясь рисунком, вычислите  , где   — одна из первообразных функции   . Решение: Разность значений первообразной в точках 8 и 2 равна площади выделенной на рисунке трапеции Поэтому

№ 27485. Прямая параллельна касательной к графику № 27485. Прямая параллельна касательной к графику функции . Найдите абсциссу точки касания. Решение: Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой их угловые коэффициенты равны. Поэтому абсцисса точки касания находится из уравнения :

№ 320180. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся. № 320180. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся. Решение:

№ 320196. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного меньше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм. № 320196. При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного меньше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм. Решение: По условию, диаметр подшипника будет лежать в пределах от 66,99 до 67,01 мм с вероятностью 0,965. Поэтому искомая вероятность противоположного события равна 1 − 0,965 = 0,035. Ответ: 0,035.

№ 500997. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе. № 500997. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе. Решение. Рассмотрим первую группу. Вероятность того, что Аня окажется в ней, равна . Если Аня уже находится в первой группе, то вероятность того, что Нина окажется этой же группе равна Поскольку все семь групп равноправны, вероятность того, что подруги окажутся в одной группе, равна Ответ: 0,1.

Приведем комбинаторное решение. Количество способов выбрать 3 учащихся из 21 учащегося класса равно Приведем комбинаторное решение. Количество способов выбрать 3 учащихся из 21 учащегося класса равно Выбрать пару «Аня и Нина» и поместить их в одну из семи групп можно 7 способами. Добавить в эту группу еще одного из оставшихся 19 учащихся можно 19 способами. Поэтому вероятность того, что девочки окажутся в одной группе равна Приведем еще одно решение. Пусть Аня оказалась в некоторой группе. Тогда Нина может попасть в ту же группу на оставшиеся 2 места с вероятностью 2:20=0,1

№ 320198. Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач. № 320198. Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач. Решение. Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B). Тогда, используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07. Ответ: 0,07.

№ 320206. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода. № 320206. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода. Решение. Для погоды на 4, 5 и 6 июля есть 4 варианта: ХХО, ХОО, ОХО, ООО (здесь Х — хорошая, О — отличная погода). Найдем вероятности наступления такой погоды: P(XXO) = 0,8·0,8·0,2 = 0,128; P(XOO) = 0,8·0,2·0,8 = 0,128; P(OXO) = 0,2·0,2·0,2 = 0,008; P(OOO) = 0,2·0,8·0,8 = 0,128. Указанные события несовместные, вероятность их сумы равна сумме вероятностей этих событий: P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392. Ответ: 0,392.

№ 500998. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах. № 500998. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах. Решение: Вероятность того, что Петя взял пятирублевую монету, затем десятирублевую, и затем еще одну десятирублевую (в указанном порядке) равна Поскольку Петя мог достать пятирублевую монету не только первой, но и второй или третьей, вероятность достать набор из одной пятирублевой и двух десятирублевых монет в 3 раза больше. Тем самым, она равна 0,6. Ответ: 0,6.

№ 285925. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? № 285925. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? Решение. В первом туре Руслан Орлов может сыграть с 26 − 1 = 25 бадминтонистами, из которых 9 — из России. Значит вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна Ответ: 0,36.

Спасибо за внимание!