Презентация на тему: Урок по теме: «Теорема Пифагора»

Пифагор – древнегреческий ученый, живший в VI веке до нашей эры. Пифагор – древнегреческий ученый, живший в VI веке до нашей эры. Вообще надо заметить, что о жизни и деятельности Пифагора, который умер две с половиной тысячи лет тому назад, нет достоверных сведений. Биографию учёного и его труды приходится реконструировать по произведениям других античных авторов, а они часто противоречат друг другу.

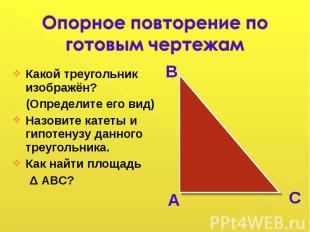
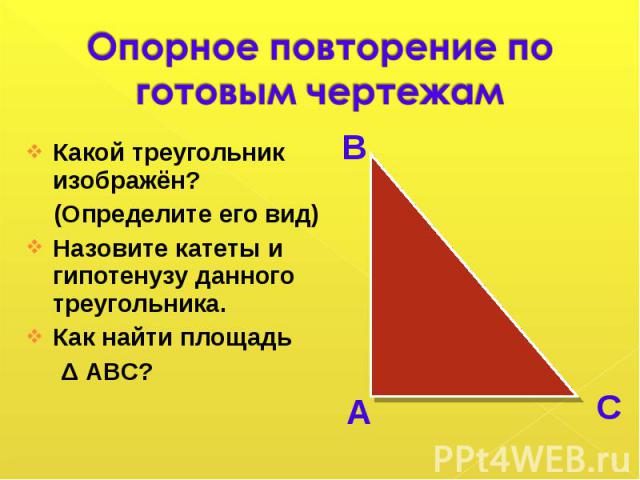
Какой треугольник изображён? Какой треугольник изображён? (Определите его вид) Назовите катеты и гипотенузу данного треугольника. Как найти площадь Δ АВС?

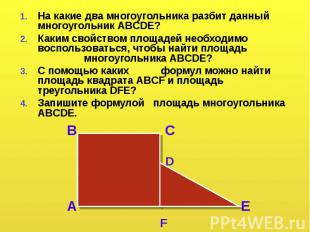
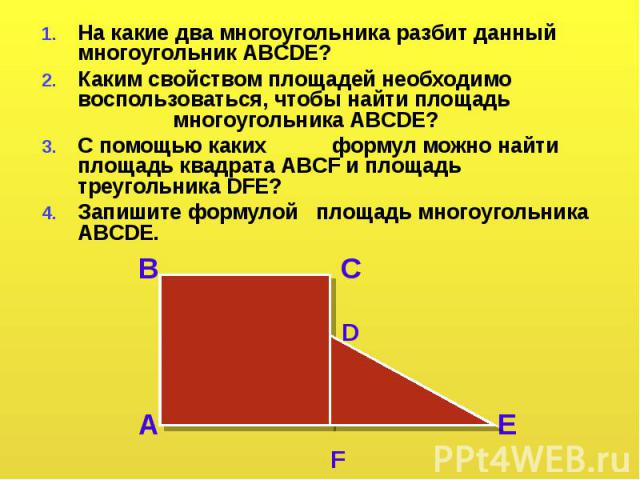
На какие два многоугольника разбит данный многоугольник ABCDE? На какие два многоугольника разбит данный многоугольник ABCDE? Каким свойством площадей необходимо воспользоваться, чтобы найти площадь многоугольника ABCDE? С помощью каких формул можно найти площадь квадрата ABCF и площадь треугольника DFE? Запишите формулой площадь многоугольника ABCDE.

Постройте в тетрадях прямоугольный треугольник (с катетами, длина которых для удобства выражается целыми числами). Измерьте катеты и гипотенузу. Результаты измерений запишите в тетрадях. Возведите все результаты в квадрат, т. е. Узнайте величины a2; b2; c2. Сложите квадраты катетов (a2 + b2) и сравните с квадратом гипотенузы. У всех ли получилось, что a2 + b2 = с2?

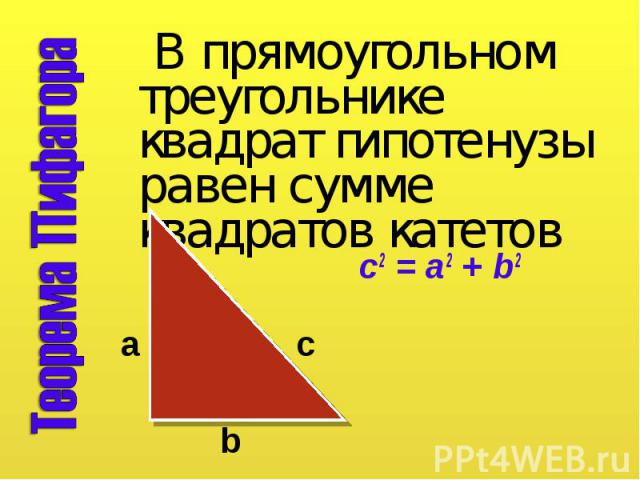
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Если дан нам треугольник, Если дан нам треугольник, И притом с прямым углом. То квадрат гипотенузы Мы всегда легко найдём: Катеты в квадрат возводим, Сумму степеней находим – И таким простым путём К результату мы придём. (И. Дырченко)

3 4 х

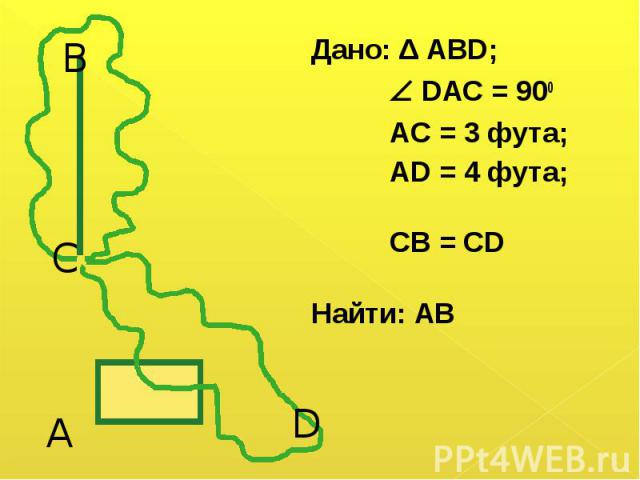
На берегу реки рос тополь одинокий. На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в том месте река В четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола. Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?

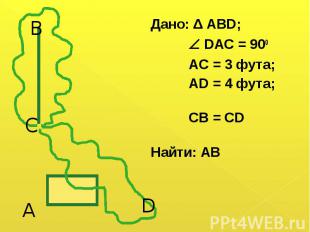
Дано: Δ АВD; Дано: Δ АВD; DAC = 900 AC = 3 фута; AD = 4 фута; CB = CD Найти: АВ

АВ = АС + СВ – по свойству длин отрезков. АВ = АС + СВ – по свойству длин отрезков. АВ = АС + CD, т. к. СВ = CD по условию. CD2 = AC2 + AD2 - по теореме Пифагора. CD2 = 32 + 42; CD = 5 АВ = 3 + 5 = 8 футов. Ответ: высота дерева 8 футов

Возможно ли было решение задач данного типа без применения теоремы Пифагора? Возможно ли было решение задач данного типа без применения теоремы Пифагора? В чём суть теоремы Пифагора? Для любых ли треугольников можно применить данную теорему?

Не знаю, чем кончу поэму, И как мне печаль избыть: Древнейшую теорему Никак я не в силах забыть. Стоит треугольник как ментор, И угол прямой в нём есть, И всем его элементам Повсюду слава и честь! Вебер

П. 54. № 483 (в, г); П. 54. № 483 (в, г); № 484 (в, г, д) № 486 (а, б)