Презентация на тему: Симметрия в жизни

Определение симметрии; Определение симметрии; Центральная симметрия; Осевая симметрия; Симметрия относительно плоскости; Симметрия вращения; Зеркальная симметрия; Симметрия подобия; Симметрия растений; Симметрия животных; Симметрия в архитектуре; Человек – существо симметричное? Симметрия слов и чисел;

СИММЕ ТРИЯ - соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости. СИММЕ ТРИЯ - соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости. (Толковый словарь Ожегова) Итак, геометрический объект считается симметричными, если с ним можно сделать что-то такое, после чего он останется неизменным.

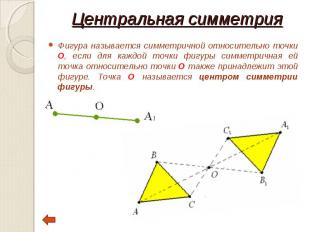
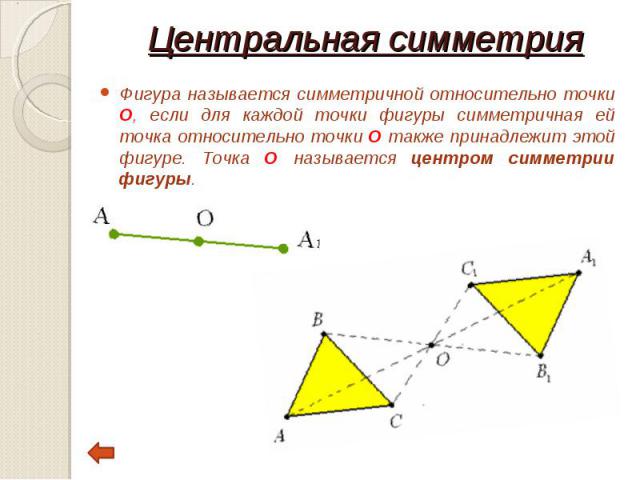
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры.

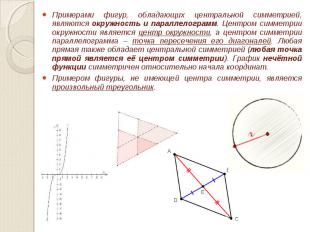
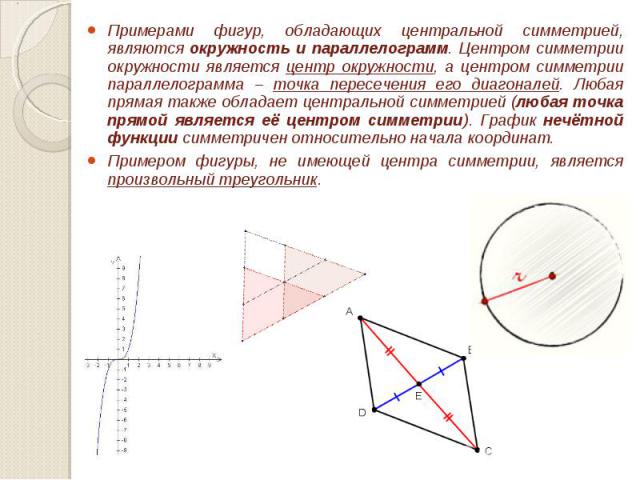
Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма – точка пересечения его диагоналей. Любая прямая также обладает центральной симметрией (любая точка прямой является её центром симметрии). График нечётной функции симметричен относительно начала координат. Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма – точка пересечения его диагоналей. Любая прямая также обладает центральной симметрией (любая точка прямой является её центром симметрии). График нечётной функции симметричен относительно начала координат. Примером фигуры, не имеющей центра симметрии, является произвольный треугольник.

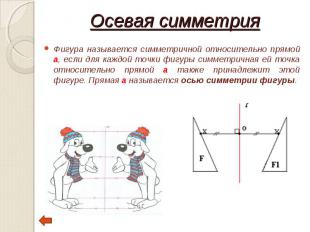
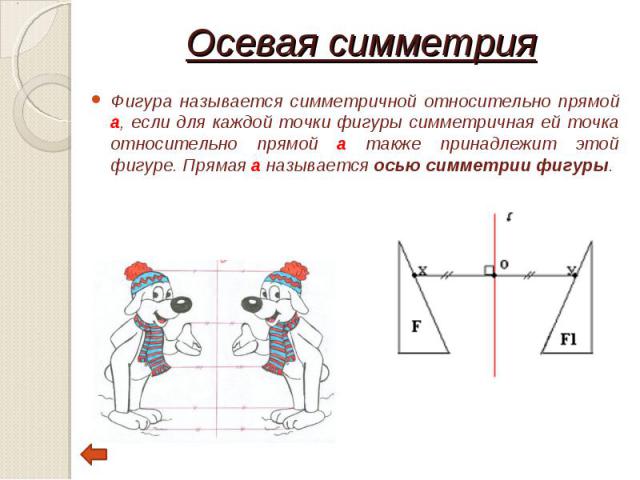
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая a называется осью симметрии фигуры. Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая a называется осью симметрии фигуры.

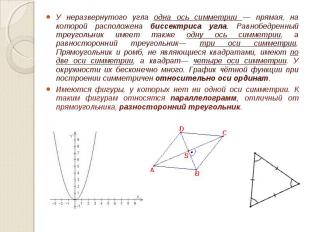
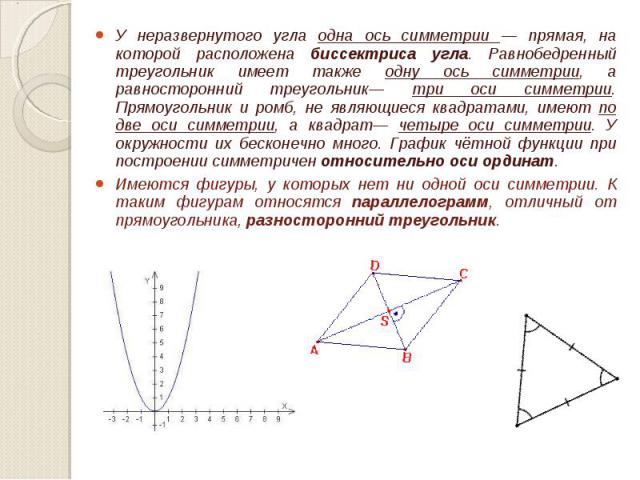
У неразвернутого угла одна ось симметрии — прямая, на которой расположена биссектриса угла. Равнобедренный треугольник имеет также одну ось симметрии, а равносторонний треугольник— три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют по две оси симметрии, а квадрат— четыре оси симметрии. У окружности их бесконечно много. График чётной функции при построении симметричен относительно оси ординат. У неразвернутого угла одна ось симметрии — прямая, на которой расположена биссектриса угла. Равнобедренный треугольник имеет также одну ось симметрии, а равносторонний треугольник— три оси симметрии. Прямоугольник и ромб, не являющиеся квадратами, имеют по две оси симметрии, а квадрат— четыре оси симметрии. У окружности их бесконечно много. График чётной функции при построении симметричен относительно оси ординат. Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

Точки А и А1 называются симметричными относительно плоскости а (плоскость симметрии), если плоскость а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости а считается симметричной самой себе. Две фигуры называются симметричными относительно плоскости (или зеркально-симметричными относительно ), если они состоят из попарно симметричных точек. Это значит, что для каждой точки одной фигуры симметричная ей (относительно ) точка лежит в другой фигуре. Точки А и А1 называются симметричными относительно плоскости а (плоскость симметрии), если плоскость а проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости а считается симметричной самой себе. Две фигуры называются симметричными относительно плоскости (или зеркально-симметричными относительно ), если они состоят из попарно симметричных точек. Это значит, что для каждой точки одной фигуры симметричная ей (относительно ) точка лежит в другой фигуре.

Тело (или фигура) обладает симметрией вращения, если при повороте на угол 360º/n, где n целое число, около некоторой прямой АВ (ось симметрии) оно полностью совмещается со своим исходным положением. Тело (или фигура) обладает симметрией вращения, если при повороте на угол 360º/n, где n целое число, около некоторой прямой АВ (ось симметрии) оно полностью совмещается со своим исходным положением. Радиальная симметрия – форма симметрии, сохраняющаяся при вращении объекта вокруг определённой точки или прямой. Часто эта точка совпадает с центром тяжести объекта, то есть той точкой, в которой пересекается бесконечное количество осей симметрии. Подобными объектами могут быть круг, шар, цилиндр или конус.

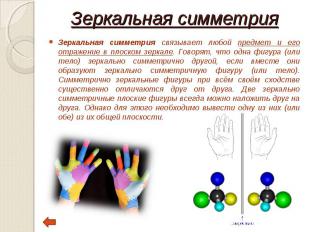
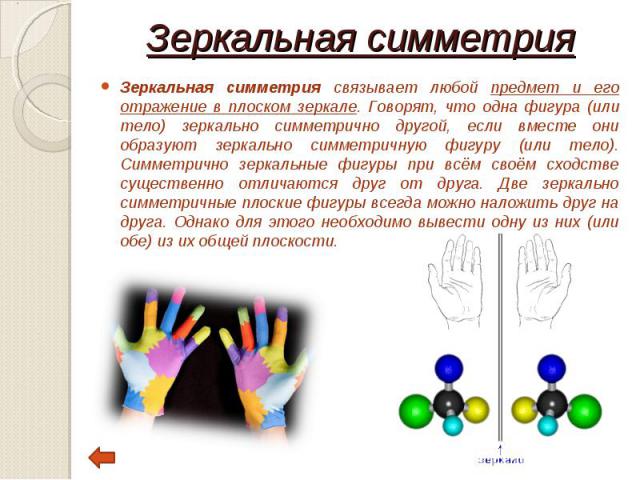
Зеркальная симметрия связывает любой предмет и его отражение в плоском зеркале. Говорят, что одна фигура (или тело) зеркально симметрично другой, если вместе они образуют зеркально симметричную фигуру (или тело). Симметрично зеркальные фигуры при всём своём сходстве существенно отличаются друг от друга. Две зеркально симметричные плоские фигуры всегда можно наложить друг на друга. Однако для этого необходимо вывести одну из них (или обе) из их общей плоскости. Зеркальная симметрия связывает любой предмет и его отражение в плоском зеркале. Говорят, что одна фигура (или тело) зеркально симметрично другой, если вместе они образуют зеркально симметричную фигуру (или тело). Симметрично зеркальные фигуры при всём своём сходстве существенно отличаются друг от друга. Две зеркально симметричные плоские фигуры всегда можно наложить друг на друга. Однако для этого необходимо вывести одну из них (или обе) из их общей плоскости.

Симметрия подобия представляют собой своеобразные аналоги предыдущих симметрий с той лишь разницей, что они связаны с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки. Симметрия подобия представляют собой своеобразные аналоги предыдущих симметрий с той лишь разницей, что они связаны с одновременным уменьшением или увеличением подобных частей фигуры и расстояний между ними. Простейшим примером такой симметрии являются матрешки. Иногда фигуры могут обладать разными типами симметрии. Например, поворотной и зеркальной симметрией обладают некоторые буквы: Ж, Н, М, О, А.

Существует много других видов симметрий, имеющих абстрактный характер. Например: Существует много других видов симметрий, имеющих абстрактный характер. Например: Перестановочная симметрия, которая состоит в том, что если тождественные частицы поменять местами, то никаких изменений не происходит; Калибровочные симметрии связаны с изменением масштаба. В неживой природе симметрия прежде всего возникает в таком явлении природы, как кристаллы, из которых состоят практически все твердые тела. Именно она и определяет их свойства. Самый очевидный пример красоты и совершенства кристаллов - это известная всем снежинка.

С симметрией мы встречаемся везде: в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы также подчиняются принципам симметрии. С симметрией мы встречаемся везде: в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы также подчиняются принципам симметрии.

Многие цветы обладают интересным свойством: их можно повернуть так, что каждый лепесток займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии. Многие цветы обладают интересным свойством: их можно повернуть так, что каждый лепесток займёт положение соседнего, цветок же совместится с самим собой. Такой цветок обладает осью симметрии. Винтовая симметрия наблюдается в расположении листьев на стеблях большинства растений. Располагаясь винтом по стеблю, листья как бы раскидываются во все стороны и не заслоняют друг друга от света, крайне необходимого для жизни растений. Билатеральной симметрией обладают также органы растений, например, стебли многих кактусов. В ботанике часто встречаются радиально симметрично построенные цветы.

Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Основными типами симметрии являются радиальная (лучевая) – ей обладают иглокожие, кишечнополостные, медузы и др.; или билатеральная (двусторонняя) - можно сказать, что каждое животное (будь то насекомое, рыба или птица) состоит из двух половин – правой и левой. Сферическая симметрия имеет место у радиолярий и солнечников. Любая плоскость, проведённая через центр, делит животное на одинаковые половинки.

Симметрия сооружения связывается с организацией его функций. Проекция плоскости симметрии — ось здания — определяет обычно размещение главного входа и начало основных потоков движения. Симметрия сооружения связывается с организацией его функций. Проекция плоскости симметрии — ось здания — определяет обычно размещение главного входа и начало основных потоков движения. Каждая деталь в симметричной системе существует как двойник своей обязательной паре, расположенной по другую сторону оси, и благодаря этому она может рассматриваться лишь как часть целого. Наиболее распространена в архитектуре зеркальная симметрия. Ей подчинены постройки Древнего Египта и храмы античной Греции, амфитеатры, термы, базилики и триумфальные арки римлян, дворцы и церкви Ренессанса, равно как и многочисленные сооружения современной архитектуры.

Для лучшего отражения симметрии на сооружениях ставятся акценты — особо значимые элементы (купола, шпили, шатры, парадные входы и лестницы, балконы и эркеры). Для лучшего отражения симметрии на сооружениях ставятся акценты — особо значимые элементы (купола, шпили, шатры, парадные входы и лестницы, балконы и эркеры). Для оформления убранства архитектуры применяют орнамент – ритмично повторяющийся рисунок, основанный на симметричной композиции его элементов и выражаемый линией, цветом или рельефом. Исторически сложилось несколько типов орнаментов на основе двух источников – природных форм и геометрических фигур. Но архитектор – прежде всего художник. И потому даже самые «классические» стили чаще использовали дисимметрию – нюансное отклонение от чистой симметрии или асимметрию – нарочито несимметричное построение.

Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы. Но сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале. Никто не усомнится, что внешне человек построен симметрично: левой руке всегда соответствует правая и обе руки совершенно одинаковы. Но сходство между нашими руками, ушами, глазами и другими частями тела такое же, как между предметом и его отражением в зеркале.

Многочисленные измерения параметров лица у мужчин и женщин показали, что правая его половина по сравнению с левой, имеет более выраженные поперечные размеры, что придает лицу более грубые черты, присущие мужскому полу. Левая половина лица имеет более выраженные продольные размеры, что придает ему плавность линий и женственность. Этот факт объясняет преимущественное желание лиц женского пола позировать перед художниками левой стороной лица, а лиц мужского пола — правой. Многочисленные измерения параметров лица у мужчин и женщин показали, что правая его половина по сравнению с левой, имеет более выраженные поперечные размеры, что придает лицу более грубые черты, присущие мужскому полу. Левая половина лица имеет более выраженные продольные размеры, что придает ему плавность линий и женственность. Этот факт объясняет преимущественное желание лиц женского пола позировать перед художниками левой стороной лица, а лиц мужского пола — правой.

Палиндром (от гр. Palindromos – бегущий обратно) – это некоторый объект, в котором задана симметрия составляющих от начала к концу и от конца к началу. Например, фраза или текст. Палиндром (от гр. Palindromos – бегущий обратно) – это некоторый объект, в котором задана симметрия составляющих от начала к концу и от конца к началу. Например, фраза или текст. Прямой текст палиндрома, читающийся в соответствии с нормальным направлением чтения в данной письменности (обычно слева направо), называется прямоходом, обратный – ракоходом или реверсом (справа налево). Некоторые числа также обладают симметрией.