Презентация на тему: НЕЛИНЕЙНЫЕ МОДЕЛИ РЕГРЕСИИ

2. Модели с распределенным лагом. Будем рассматривать динамические эконометрические модели. Эконометрическая модель является динамической, если в данный момент времени t она учитывает значения входящих в нее переменных, относящиеся как к текущим, так и к предыдущим моментам времени, т.е. если эта модель отражает динамику исследуемых переменных в каждый момент времени.

Будем рассматривать модели, в которых значения переменных за прошлые периоды времени (лаговые переменные) непосредственно включены в модель (присутствуют в явном виде). Это модели с распределенным лагом.

Если значение результативного признака в текущий момент времени t формируется под воздействием ряда факторов, действовавших в прошлые моменты времени t – 1, t – 2, … , t – l, то величину l, характеризующую запаздывание в воздействии фактора на результат, называют лагом, а временные ряды самих факторных переменных, сдвинутые на один или более моментов времени, – лаговыми переменными.

Разработка экономической политики как на макро-, так и на микроуровне требует решения обратного типа задач, т.е. задач, определяющих, какое воздействие окажут значения управляемых переменных текущего периода на будущие значения экономических показателей.

Эконометрическое моделирование охарактеризованных выше процессов осуществляется с применением моделей, содержащих не только текущие, но и лаговые значения факторных переменных. Эти модели называются моделями с распределенным лагом. Например, yt = a + b0xt + b1xt-1 + b2xt-2 + εt – модель с распределенным лагом.

Наряду с лаговыми значениями независимых, или факторных, переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые моменты или периоды времени. Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии. Например, модель вида yt = a + b0xt + c1yt-1 + εt – модель авторегрессии.

Построение моделей с распределенным лагом и моделей авторегрессии имеет свою специфику. Во-первых, оценка параметров модели авторегрессии, а в большинстве случаев и моделей с распределенным лагом не может быть произведена с помощью обычного МНК ввиду нарушения его предпосылок и требует специальных статистических методов.

Во-вторых, исследователям приходится решать проблемы выбора оптимальной величины лага и определения его структуры. Наконец, в-третьих, между моделями с распределенным лагом и моделями авторегрессии существует определенная взаимосвязь, и в некоторых случаях необходимо осуществлять переход от одного типа моделей к другому.

3. Лаги Алмон. Рассмотрим общую модель с распределенным лагом, имеющую конечную максимальную величину лага l, которая описывается соотношением yt = a + b0xt + b1xt-1 + … + bpxt-p + εt (1) Эта модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной х, то это изменение будет влиять на значения переменной у в течение l следующих моментов времени.

Коэффициент регрессии b0 при переменной xt характеризует среднее абсолютное изменение yt при изменении xt на 1 ед. своего измерения в некоторый фиксированный момент времени t без учета воздействий лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.

В момент (t + 1) совокупное воздействие факторной переменной xt на результат уt составит (b0 + b1) усл. ед., в момент (t + 2) это воздействие составит (b0 + b1 + b2) и т.д. Полученные таким образом суммы называют промежуточными мультипликаторами.

С учетом конечной величины лага можно сказать, что изменение переменной xt в момент t на 1 усл. ед. приведет к общему изменению результата через l моментов времени на (b0 + b1 + … +bl) абсолютных единиц. Величину b = b0 + b1 + … + bl называют долгосрочным мультипликатором.

Он показывает абсолютное изменение результата у в долгосрочном периоде t + l под влиянием изменения фактора х на 1 ед.

Предположим, что было установлено, что в исследуемой модели имеет место полиномиальная структура лага, т.е. зависимость коэффициентов регрессии bi от величины лага описывается полиномом k-ой степени. Частным случаем полиномиальной структуры лага является линейная модель. Лаги, структуру которых можно описать с помощью полиномов, называют лагами Алмон, по имени Ш. Алмон, впервые обратившей внимание на такое представление лагов.

Формально модель зависимости коэффициентов bj от величины лага j в форме полинома можно записать в следующем виде: – для полинома 1-й степени: bj = c0 + c1j; – для полинома 2-й степени: bj = c0 + c1j + с2j2; – для полинома 3-й степени: bj = c0 + c1j + с2j2 + c3j3 и т.д.

В наиболее общем виде для полинома k-ой степени имеем: bj = c0 + c1j + с2j2 + … + ckjk . Тогда каждый из коэффициентов модели (1) можно выразить следующим образом:

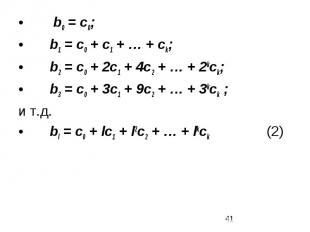
b0 = c0; b1 = c0 + c1 + … + ck; b2 = c0 + 2c1 + 4c2 + … + 2kck; b3 = c0 + 3c1 + 9c2 + … + 3kck ; и т.д. bl = c0 + lc1 + l2c2 + … + lkck (2)

Подставив в (1) найденные соотношения для bj, получим: yt = a + c0xt + (c0 + c1 + … + ck)xt-1 + (c0 + 2c1 + 4c2 + … + 2kck)xt-2 + ( c0 + 3c1 + 9c2 + … + 3kck)xt-3 + … +( c0 + lc1 + l2c2 + … + lkck)xt-l + εt . (3) Перегруппируем слагаемые в (3): yt = a + c0(xt + xt-1 + xt-2 + … + xt-l) + c1(xt-1 + 2xt-2 + 3xt-3 + … + lxt-l) + c2(xt-1 + 4xt-2 + 9xt-3 + … + l2xt-l) + … + ck(xt-1 + 2kxt-2 + 3kxt-3 + … + lkxt-l) + εt . (4)

Обозначим слагаемые в скобках при сi как новые переменные: z0 = xt + xt-1 + xt-2 + … + xt-l = z1 = xt-1 + 2xt-2 + 3xt-3 + … + lxt-l = z2 = xt-1 + 4xt-2 + 9xt-3 + … + l2xt-l = (5) ………………………………………………. zk = xt-1 + 2kxt-2 + 3kxt-3 + … + l2xt-l =

Перепишем модель (4) с учетом соотношений (5): yt = a + c0z0 + c1z1 + c2z2 + … + ckzk + εt 6)

Процедура применения метода Алмон для расчета параметров модели с распределенным лагом 1. Определяется максимальная величина лага l. 2. Определяется степень полинома k, описывающего структуру лага. 3. По соотношениям (5) рассчитываются значения переменных z0, … ,zk.

Определяются параметры уравнения линейной регрессии (6). С помощью соотношений (2) рассчитываются параметры исходной модели с распределенным лагом.

Применение метода Алмон сопряжено с рядом проблем. 1. Величина лага l должна быть известна заранее. При ее определении лучше исходить из максимально возможного лага, чем ограничиваться лагами небольшой длины. Выбор меньшего лага, чем его реальное значение, приведет к тому, что в модели регрессии не будет учтен фактор, оказывающий значительное влияние на результат, т.е. к неверной спецификации модели.

Влияние этого фактора в такой модели будет выражено в остатках. Тем самым в модели не будут соблюдаться предпосылки МНК о случайности остатков, а полученные оценки ее параметров окажутся неэффективными и смещенными.

Выбор большей величины лага по сравнением с ее реальным значением будет означать включение в модель статистически незначимого фактора и снижение эффективности полученных оценок, однако эти оценки все же будут несмещенными.

Наиболее простым способом определения реальной величины лага является измерение тесноты связи между результатом и лаговыми значениями фактора. Кроме того, оптимальную величину лага можно приближенно определить на основе априорной информации экономической теории или проведенных ранее эмпирических исследований.

2. Необходимо установить степень полинома k. Обычно на практике ограничиваются рассмотрением полиномов 2-й и 3-й степени, применяя следующее правило: выбранная степень полинома должна быть на единицу больше числа экстремумов в структуре лага. Если априорную информацию о структуре лага получить невозможно, величину k проще всего получить путем сравнения моделей, построенных для различных значений k, и выбора наилучшей модели.

3. Переменные z, которые определяются как линейные комбинации исходных переменных х, будут коррелировать между собой в случаях, когда наблюдается высокая связь между самими исходными переменными. Поэтому оценку параметров модели (6) приходится проводить в условиях мультиколлинеарности факторов.

Однако мультиколлинеарность факторов z0, … , zk в модели (6) сказывается на оценках параметров b0, … , bl в несколько меньшей степени, чем если бы эти оценки были получены путем применения обычного МНК непосредственно к модели (1) в условиях мультиколлинеарности факторов xt, … , xt-l.

Метод Алми имеет два преимущества. 1. Он достаточно универсален и может быть применен для моделирования процессов, которые характеризуются разнообразными структурами лагов. 2. При относительно небольшом количестве переменных в (6) (обычно выбирают k = 2 или k = 3), которое не приводит к потере значительного числа степеней свободы, с помощью метода Алмон можно построить модели с распределенным лагом любой длины.

4. Модель Койка. Рассмотренные модели были построены в предположении конечной длины лага l. Предположим, что для описания некоторого процесса используется модель с бесконечным лагом вида yt = a + b0xt + b1xt-1 + b2xt-2 + … + εt. (7)

Параметры такой модели обычным МНК определить нельзя из-за бесконечного числа факторов. Однако, приняв определенные допущения относительно структуры лага, оценки ее параметров все же можно получить. Эти допущения состоят в наличии геометрической структуры лага, т.е. такой структуры, когда воздействия лаговых значений фактора на результат уменьшаются с увеличением величины лага в геометрической прогрессии.

Впервые такой подход к оценке параметров моделей с распределенным лагом был предложен Л.М. Койком. Койк предположил, что существует некоторый постоянный темп λ (0 < λ < 1) уменьшения во времени лаговых воздействий фактора на результат. Если, например, в период t результат изменялся под воздействием изменения фактора в этот же период времени на b0 ед., то под воздействием изменения фактора, имевшего место в период (t – 1), результат изменится на b0λ ед.; в период (t – 2) – на b0λ2 ед., и т.д.

Для некоторого периода (t – l) это изменение результата составит b0λl ед. В более общем виде можно записать: bj = b0 λ; j = 0, 1, 2, … , 0<λ<1 (8) Ограничение на значения λ > 0 обеспечивает одинаковые знаки для всех коэффициентов bj > 0, а ограничение bj < 1 означает, что с увеличением лага значения параметров модели ( 7) убывают в геометрической прогрессии.

Чем ближе λ к нулю, тем выше темп снижения воздействия фактора на результат во времени и тем большая доля воздействия на результат приходится на текущие значения фактора хt.

Выразим с помощью (8) все коэффициенты bj в модели (7) через b0 и λ: yt = a + b0xt + b0 λxt-1 + b0 λ2xt-2 + … + εt (9) Тогда для периода (t – 1) модель (9) можно записать следующим образом: yt-1 = a + b0xt-1 + b0λxt-2 + b0λ2xt-3 + … + εt-1 10) Умножим обе части (10) на λ: λyt-1 =λ a + b0 λxt-1 + b0λ2 xt-2 + b0λ3 xt-3 + … +λ εt-1 (11)

Вычтем найденное соотношение (11) из соотношения (9): yt – λyt-1 = a – λa + b0 xt + εt-1 - λ εt-1 (12) Преобразовав (12), получим модель Койка: yt = a(1 – λ) + b0 xt + (1 – λ)yt-1 + ut , (13) где ut = εt – λεt-1.

Полученная модель есть модель двухфакторной линейной регрессии (точнее – авторегрессии). Определив ее параметры, мы найдем λ и оценки параметров а и b0 исходной модели. Далее с помощью соотношений (8) можно определить параметры b1, b2, … модели (7). Отметим, что применение обычного МНК к оценке параметров модели (13) приведет к получению смещенных оценок ее параметров ввиду наличия в этой модели в качестве фактора лаговой результативной переменной yt-1.

Описанный алгоритм получил название преобразования Койка. Это преобразование позволяет перейти от модели с бесконечными распределенными лагами к модели авторегрессии, содержащей две независимые переменные: xt и yt-1.

Несмотря на бесконечное число лаговых переменных в модели (7), геометрическая структура лага позволяет определить величины среднего и медианного лагов в модели Койка. Поскольку сумма коэффициентов регрессии в модели (7) есть сумма геометрической прогрессии, т.е. (14)

то средний лаг определяется как (15)

Нетрудно заметить, что при λ = 0,5 средний лаг , а при l < 0,5 средний лаг , т.е. воздействие фактора на результат в среднем занимает менее одного периода времени. Величину (1 – λ) интерпретируют обычно как скорость, с которой происходит адаптация результата во времени к изменению факторного признака. Для расчета медианного лага необходимо

выполнение следующего условия: Поэтому медианный лаг в модели Койка равен