Презентация на тему: Производная Изучение нового материала по теме

ПРОИЗВОДНАЯ КОЛПАКОВА С. В.
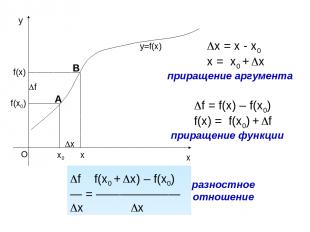
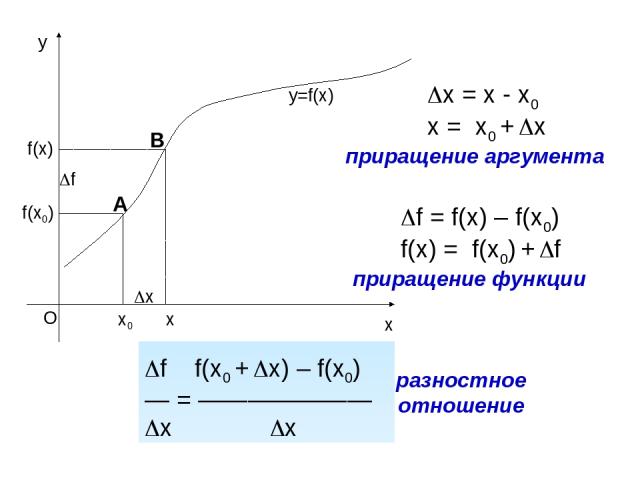
x0 x f(x0) x f(x) f y=f(x) x = x - x0 x = x0 + x приращение аргумента f = f(x) – f(x0) f(x) = f(x0) + f приращение функции f f(x0 + x) – f(x0) — = ——————— x x разностное отношение А В
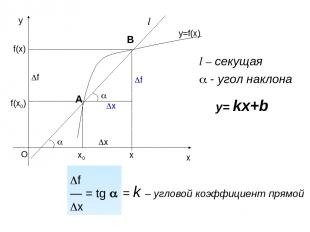
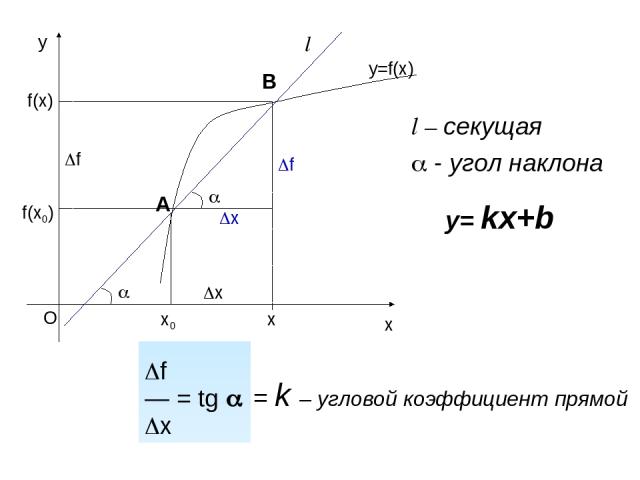
f(x0) f(x) x f l l – секущая - угол наклона f — = tg x = k – угловой коэффициент прямой y= kx+b

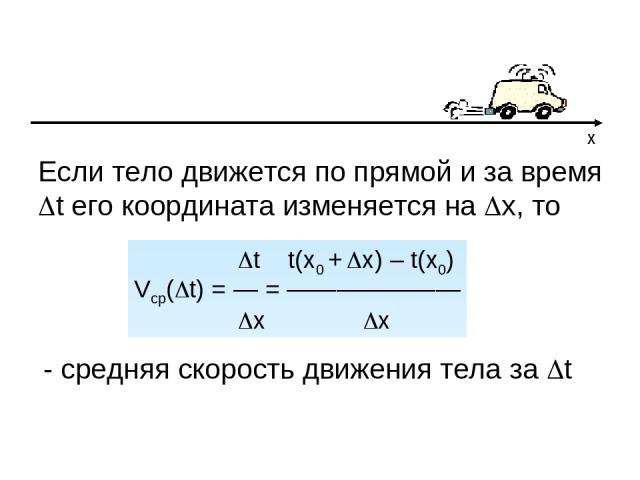
x Если тело движется по прямой и за время t его координата изменяется на x, то t t(x0 + x) – t(x0) Vср( t) = — = ——————— x x - средняя скорость движения тела за t
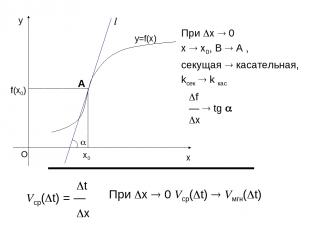
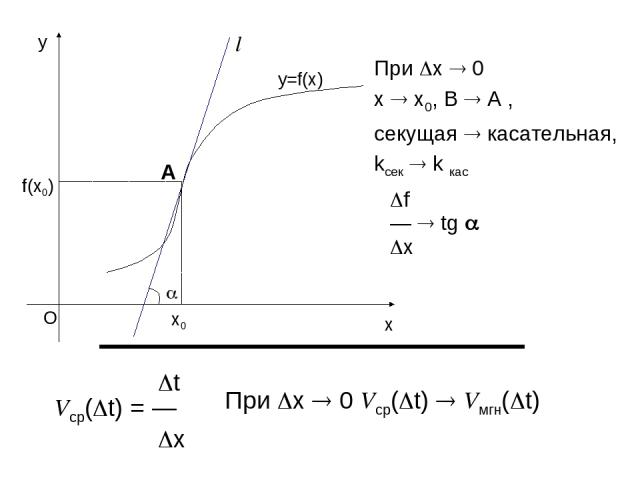
При x 0 x x0, B A , секущая касательная, kсек k кас f — tg x t Vср( t) = — x При x 0 Vср( t) Vмгн( t)

Производная Производной функции f в точке x0 называется число, к которому стремится разностное отношение при x 0. f f(x0 + x) – f(x0) f´(x0)= — = ——————— x x при x 0.

Правила вычисления производных Если функции U и V дифференцируемы в точке x0, то Если функция U дифференцируема в точке x0, а С-постоянная, то (СU)´=CU´

Формулы для вычисления производных



Ответы: