Презентация на тему: пирамиды и ёе сечение

Пирамиды и её сечения.

Пирамиды •

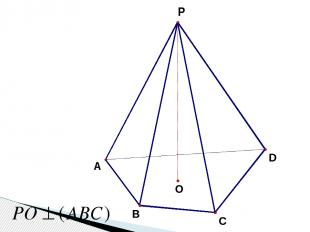
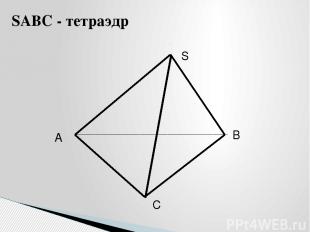
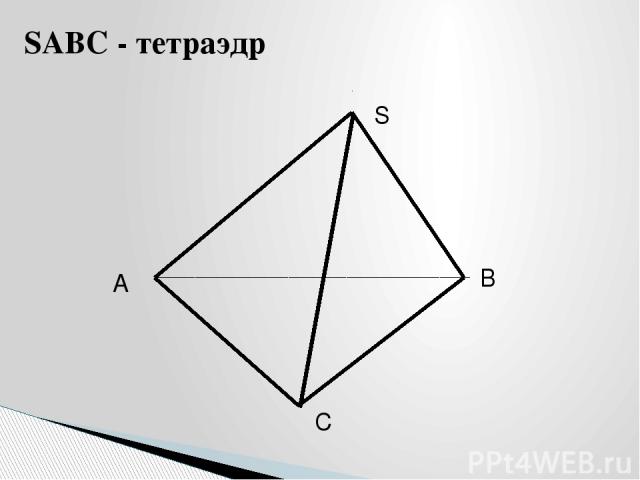
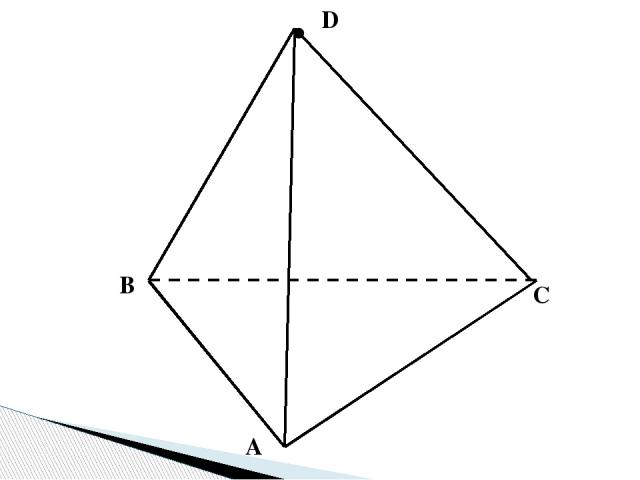
A B C S SABC - тетраэдр

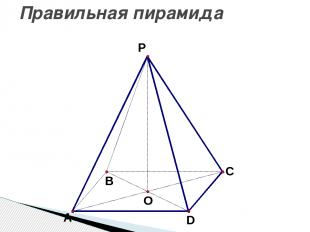
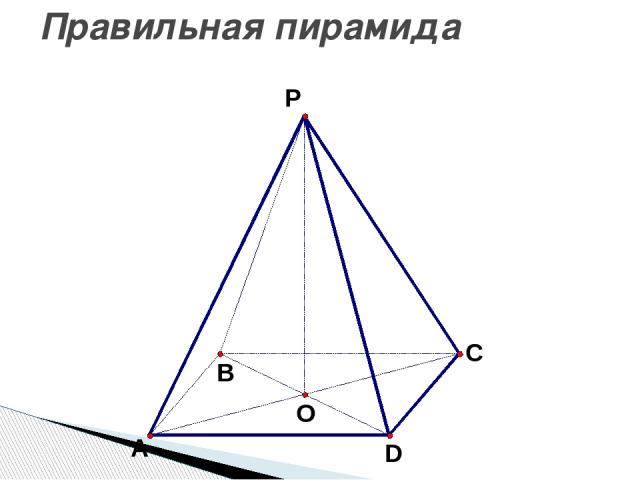
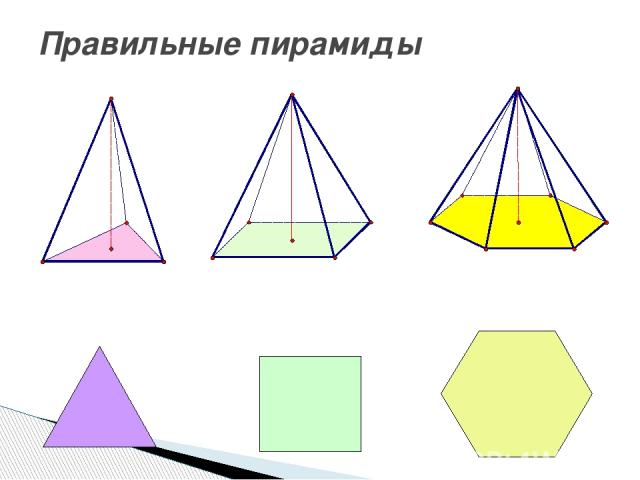
Правильная пирамида

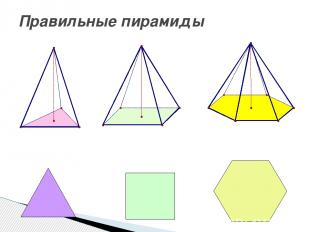
Правильные пирамиды

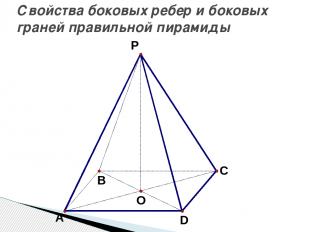
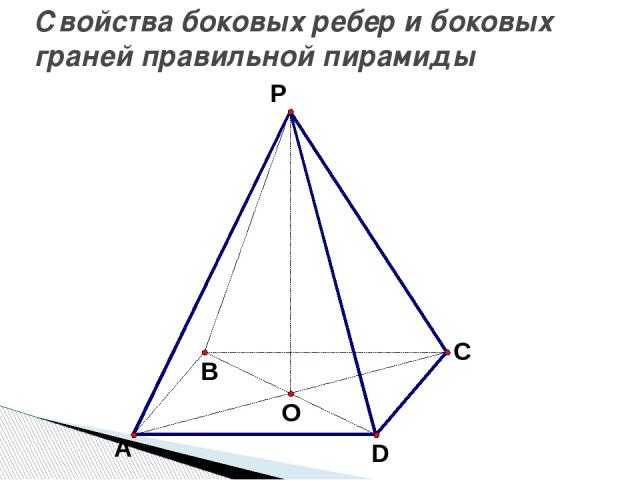
Свойства боковых ребер и боковых граней правильной пирамиды

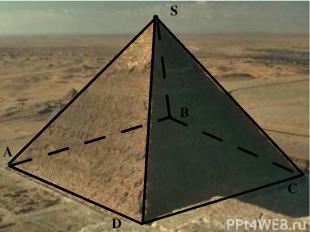
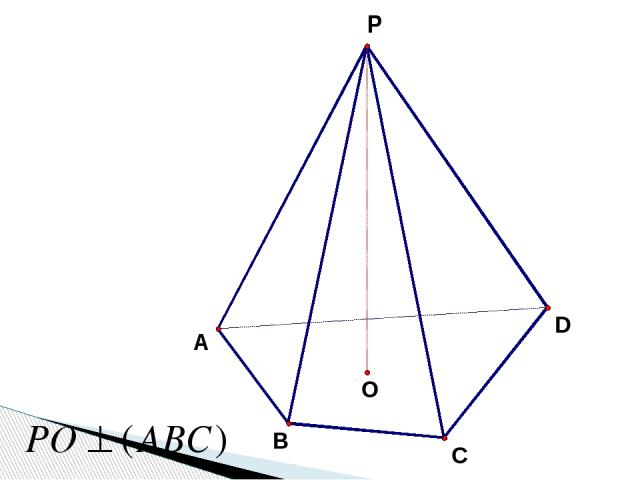
S В D С А •

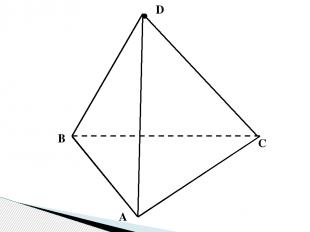
• D С В А

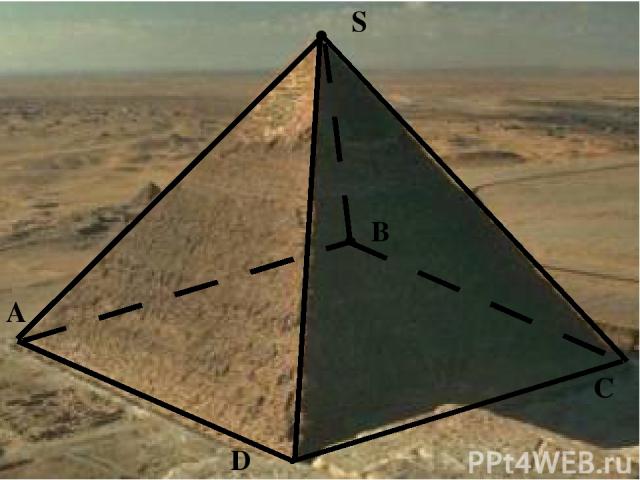
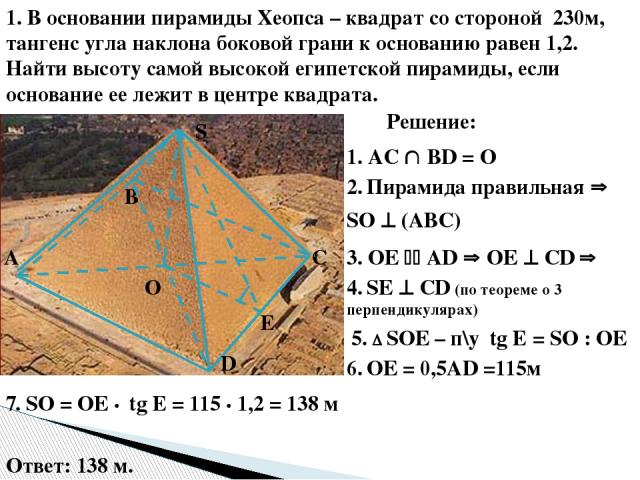
1. В основании пирамиды Хеопса – квадрат со стороной 230м, тангенс угла наклона боковой грани к основанию равен 1,2. Найти высоту самой высокой египетской пирамиды, если основание ее лежит в центре квадрата. О E S D С В А Решение: 1. AC ВD = О 2. Пирамида правильная SО (АВС) 3. ОЕ АD ОЕ СD 4. SЕ СD (по теореме о 3 перпендикулярах) 5. SОЕ – п\у tg E = SО : ОЕ 6. ОЕ = 0,5АD =115м 7. SО = ОЕ • tg E = 115 • 1,2 = 138 м Ответ: 138 м.

2. В основании пирамиды Хеопса – квадрат со стороной 230м, высота пирамиды 138 м. Найти боковое ребро самой высокой египетской пирамиды. О 230 м S D С В А Решение: 1. AC ВD = О 3. Пирамида правильная SО (АВС) 4. SОD – п\у по т. Пифагора DS2 = DО2+ОS2 = 26450 + 1382= = 26450 +19044 = 45494 DS 213 м Ответ: 213 м. 2. АОD – п\у, р\б по т. Пифагора АD2 = DО2+ОА2 2ОD2= 2302 = 52900 ОD2 = 26450

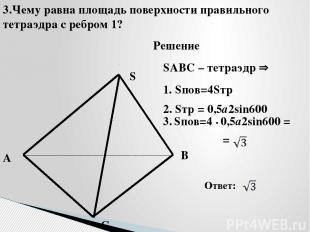
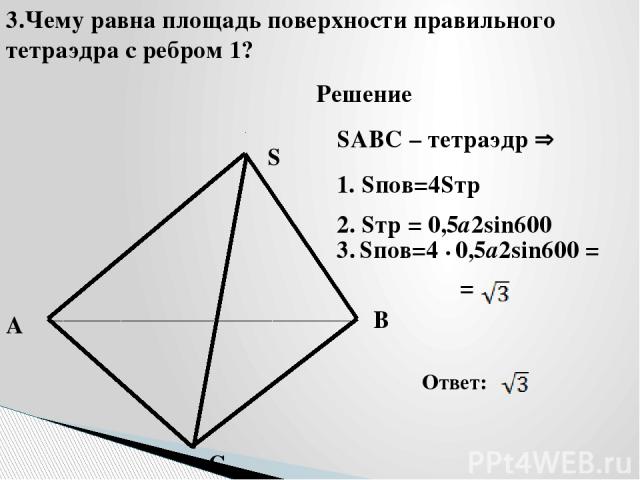
A B C S SABC – тетраэдр 3.Чему равна площадь поверхности правильного тетраэдра с ребром 1? Решение 1. Sпов=4Sтр 2. Sтр = 0,5а2sin600 Ответ: 3. Sпов=4 • 0,5а2sin600 = =

4. Найдите площадь боковой поверхности пирамиды Хеопса, сторона основания которой равна 230 м и высота 138 м. О E S D С В А Решение: 2. AC ВD = О 3. Пирамида правильная SО (АВС) 4. ОЕ СD ОЕ АD 5. SЕ АD (по теореме о 3 перпендикулярах) 6. SОЕ – п\у по т. Пифагора ЕS2 = ЕО2+ОS2 = 1152 + 1382 = = 13225 +19044 = 32269 ЕS 180 7. ES - высота АSD SАSD = 0,5 ЕS•АD = 0,5 •180 • 230 =20700 м2 Ответ: 82800 м2 1. Sб.пов=4Sтр 8. Sб.пов=4Sтр = 4 • 20700 = 82800 м2

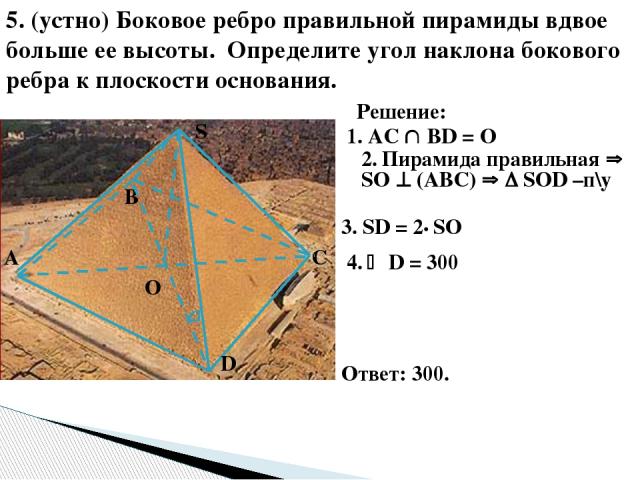
5. (устно) Боковое ребро правильной пирамиды вдвое больше ее высоты. Определите угол наклона бокового ребра к плоскости основания. О S D С В А Решение: 1. AC ВD = О 2. Пирамида правильная SО (АВС) SОD –п\у 4. D = 300 Ответ: 300. 3. SD = 2• SO

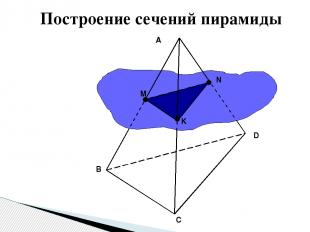
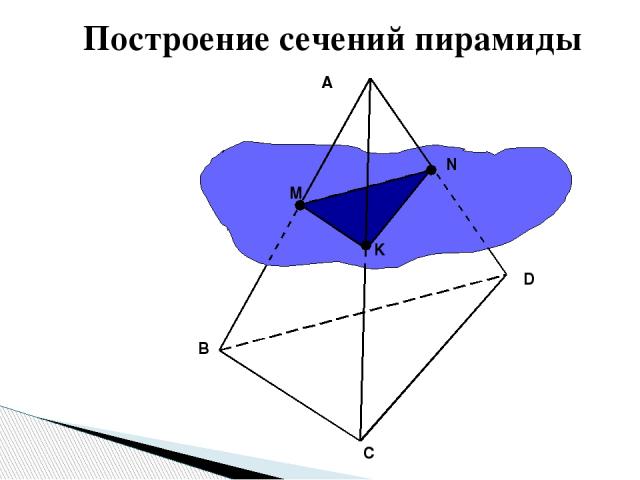
A B C D M N K α Построение сечений пирамиды

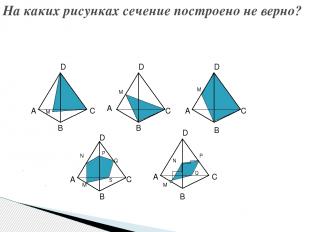
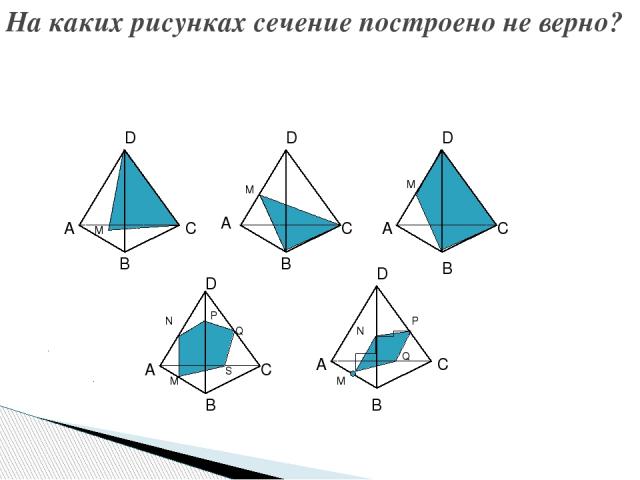
На каких рисунках сечение построено не верно? B А А А А А D D D D D B B B B C C C C C N M M M M M N Q P P Q S

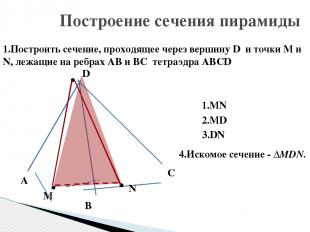
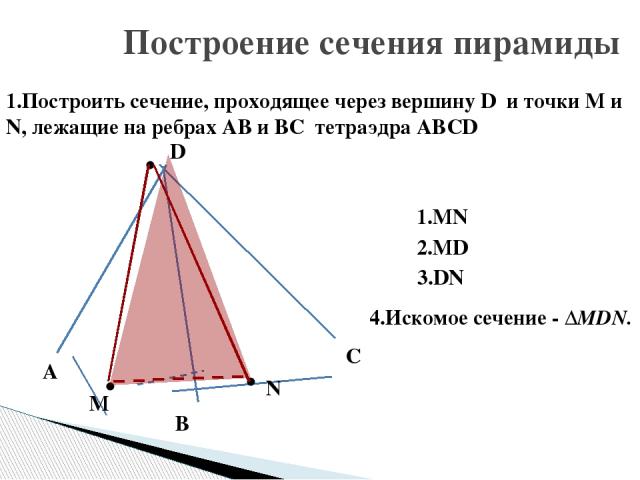
Построение сечения пирамиды 1.Построить сечение, проходящее через вершину D и точки М и N, лежащие на ребрах AB и BC тетраэдра ABCD 1.MN 2.MD 3.DN 4.Искомое сечение - ∆MDN. • • • M N B A D C

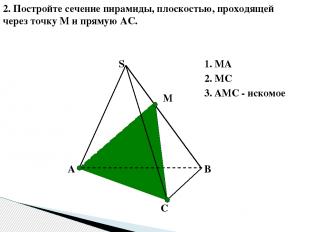
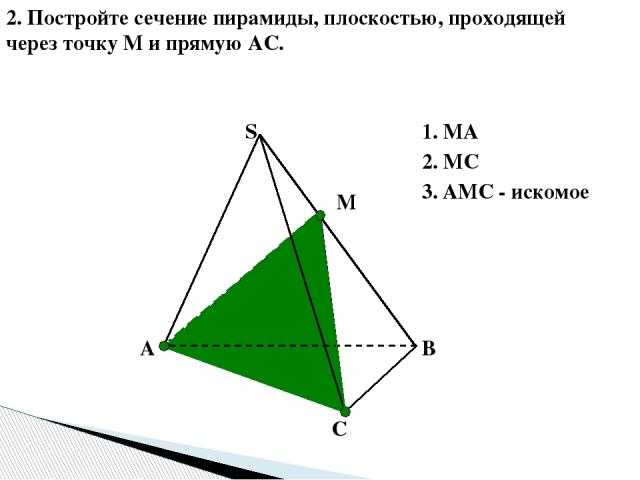
В А С S 2. Постройте сечение пирамиды, плоскостью, проходящей через точку М и прямую АС. М 1. МА 2. МС 3. АМС - искомое А↔М, т.к.А є( ABS) и М є (ABS) С↔М, т.к.Сє( СBS) и М є (СBS) АМС- искомое сечение. ( по т.15.1)

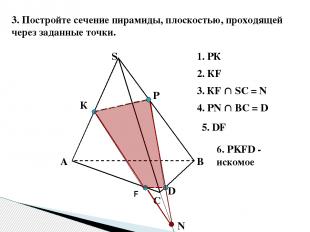
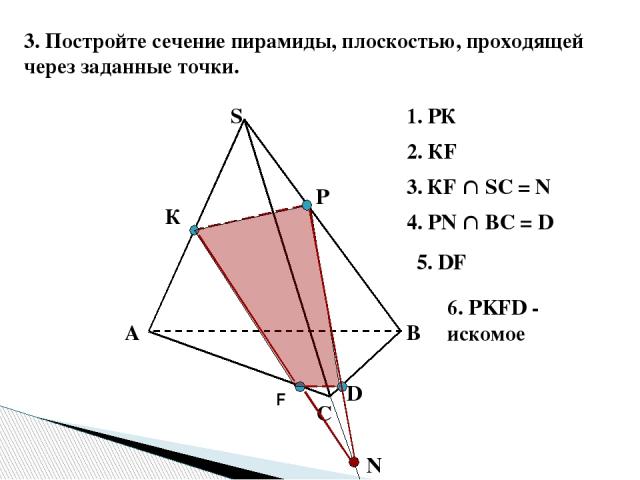
3. Постройте сечение пирамиды, плоскостью, проходящей через заданные точки. В А С S К Р F 1. РК 2. КF 3. КF SС = N N 4. РN ВС = D D 5. DF 6. PKFD - искомое

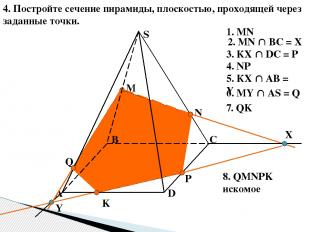
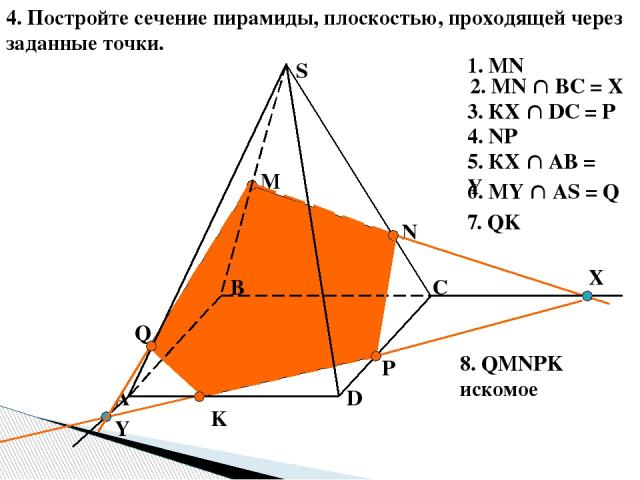
4. Постройте сечение пирамиды, плоскостью, проходящей через заданные точки. А B C D S M N K X P Y Q 1. MN 2. MN ВС = Х 3. КХ DС = Р 4. NP 5. КХ АВ = Y 6. MY AS = Q 7. QK 8. QMNPK искомое

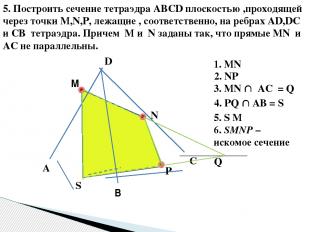
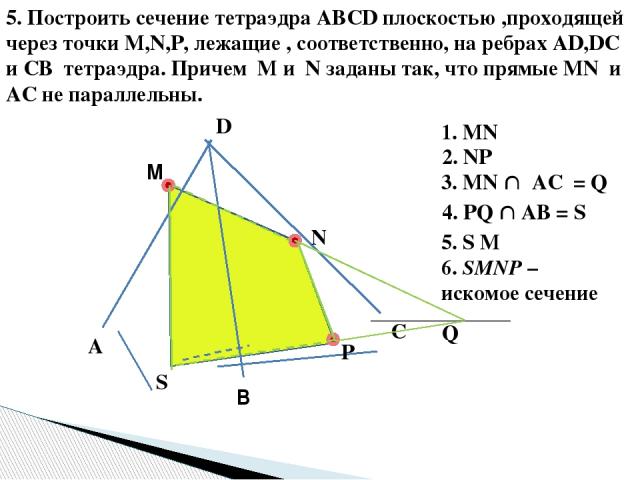
5. Построить сечение тетраэдра ABCD плоскостью ,проходящей через точки M,N,P, лежащие , соответственно, на ребрах AD,DC и CB тетраэдра. Причем M и N заданы так, что прямые MN и AC не параллельны. В М N Р 1. MN 2. NP 3. MN AC = Q Q 4. PQ AB = S S 5. S M 6. SMNP – искомое сечение A D C

1). Если в правильной треугольной пирамиде высота H равна стороне основания a, то боковые ребра составляют с плоскостью основания углы в 600. Верно ли это утверждение? 2). Сторона квадрата равна 10 см. Доказать, что нельзя, используя его в качестве основания, построить правильную четырехугольную пирамиду с боковым ребром 7 см. 3). Доказать или опровергнуть утверждение: «если в пирамиде все ребра равны, то пирамида правильная». Домашнее задание

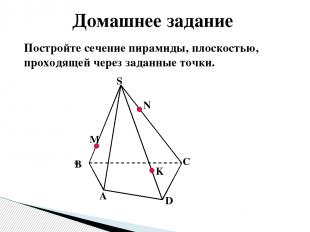
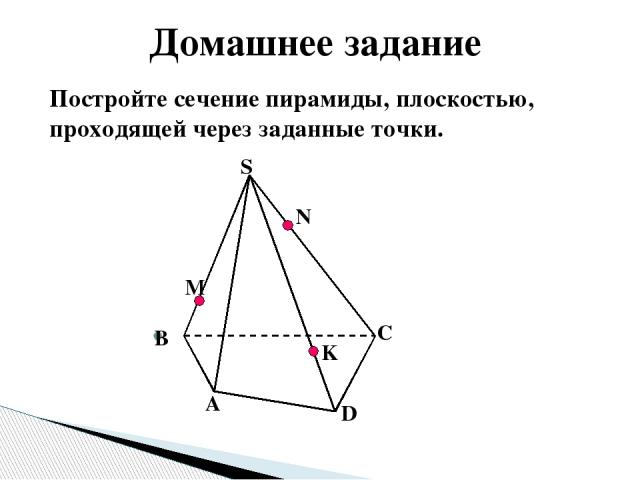
Постройте сечение пирамиды, плоскостью, проходящей через заданные точки. М N K A B C D S Домашнее задание