Презентация на тему: Медиана треугольника

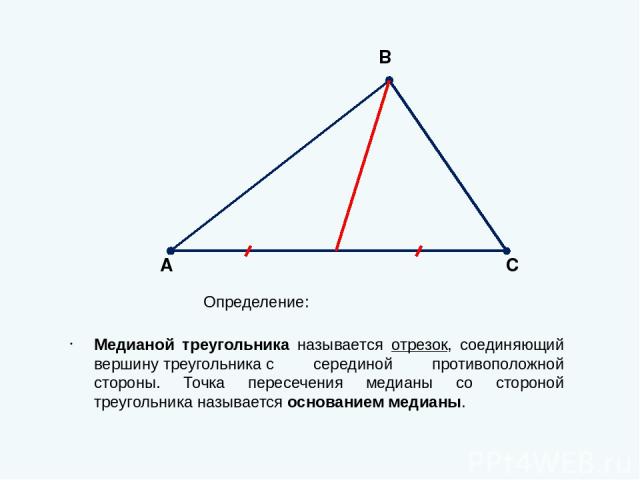
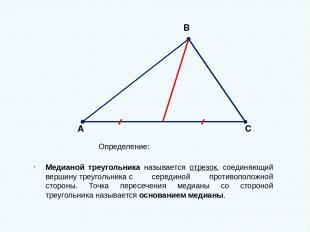
Определение: Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Точка пересечения медианы со стороной треугольника называется основанием медианы. А В С

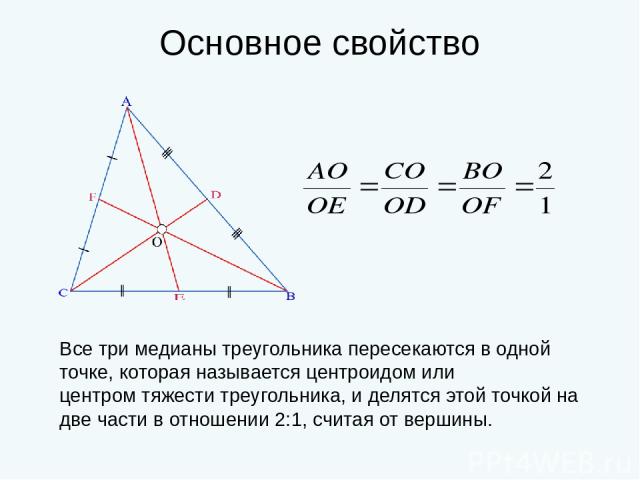
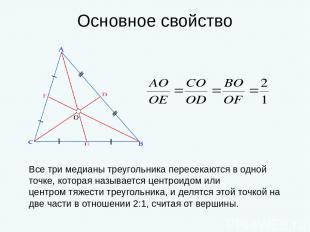
Основное свойство Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или  центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

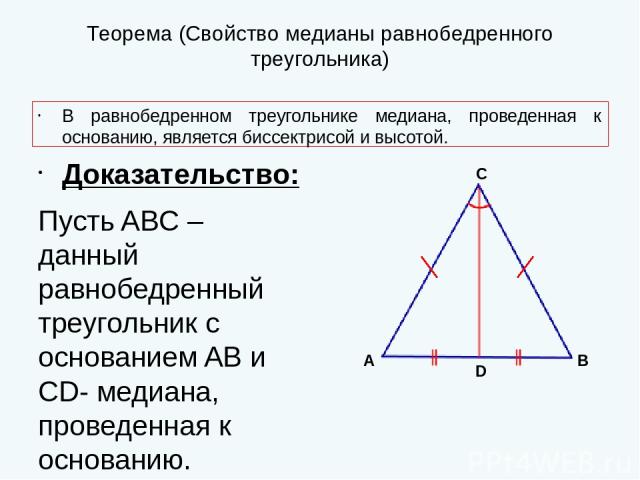
Теорема (Свойство медианы равнобедренного треугольника) В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. Доказательство: Пусть ABC – данный равнобедренный треугольник с основанием AB и CD- медиана, проведенная к основанию. ∆CAD =∆CBD (по 1 признаку равенства треугольников) . ∠ACD = ∠BCD. Поэтому CD – биссектриса. ∠ADC = ∠BDC и смежные, поэтому CD – высота треугольника. Теорема доказана. C A B D

Другие свойства Медиана разбивает треугольник на два равновеликих (по площади) треугольника. Треугольник делится тремя медианами на шесть равновеликих треугольников. В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы. Большей стороне треугольника соответствует меньшая медиана.

Основные соотношения Если известны все стороны треугольника (знаемa, b, c) Если известны все медианы (знаемm_a, m_b, m_c) m_c–медиана к стороне с

Решение задач

Решение задач В треугольнике ABC стороны AB, BC и CA равны соответственно 4, 5, 7. Найти все медианы треугольника. Известно, что в треугольнике abc медиана m_a = , m_b = , m_c = . Найти стороны треугольника. Ответ: 1 вариант 2 вариант Ответ: a = 4, b = 6, c = 7

Домашнее задание Учебник: Л. С. Атанасян «Геометрия 7-9» №106, 109, 114

Спасибо за внимание!