Презентация на тему: математика и исскуство

«Математика и искусство.»

Великая книга природы написана математическими символами. Галилей

Математика – царица всех наук, символ мудрости. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства. Это не только стройная система законов, теорем и задач, но и уникальное средство познания красоты.

Искусство – -творческое отражение, воспроизведение действительности в художественных образах. Искусство существует и развивается как система взаимосвязанных между собой видов, многообразие которых обусловлено многогранностью самого реального мира, отображаемого в процессе художественного творчества.

Конечно же, все законы красоты невозможно вместить в несколько формул. Но, изучая математику мы открываем всё новые и новые слагаемые прекрасного, приближаясь к пониманию, а в дальнейшем и к созданию красоты и гармонии. Искусство, наука, красота… эти великие сферы человеческой деятельности, внешне столь разные и далекие друг от друга, тесно переплетены между собой незримыми узами! И разорвать эти узы нельзя, не повредив и тому и другому. Красота является самым крепким связующим звеном между наукой и искусством!

Виды искусств Наиболее распространенной схемой является деление искусства на три группы. пространственные или пластические виды искусств:Изобразительное искусство, Декоративно-прикладное искусство, Архитектура, Фотография. временные или динамические виды искусств:Музыка, Литература пространственно-временные виды, которые называются также синтетическими или зрелищными искусствами:Хореография, Литература, Театральное искусство, Киноискусство.

Существование различных видов искусств вызвано тем, что ни одно из них своими собственными средствами не может дать художественную всеобъемлющую картину мира. Такую картину может создать только вся художественная культура человечества в целом, состоящая из отдельных видов искусства.

«Потребность красоты и творчества, воплощающего ее, - неразлучна с человеком, и без нее человек, быть может, не захотел бы жить на свете». Ф. М. Достоевский

Красота скульптуры, храма, картины, симфонии, поэмы... Что между ними общего? Разве можно сравнивать красоту храма с красотой музыки? Оказывается можно, если будут найдены единые критерии прекрасного, если будут открыты общие формулы красоты, объединяющие понятие прекрасного самых различных объектов - от цветка ромашки до красоты обнаженного человеческого тела.

Существуют ли объективные законы прекрасного? Нельзя отрицать заглавную роль симметрии в природе, которая обязана своим существованием вечному закону природы - закону тяготения. В основе основ музыки и архитектуры- гамме и пропорции – лежит математика, в частности ряд золотого сечения и модулор Ле Корбюзье. В изобразительном искусстве используется общая теория перспективы.

“Симметрия, как бы широко или узко мы не понимали это слово, есть идея, с помощью которой человек пытался объяснить и создать порядок, красоту и совершенство" Герман Вейль

К фундаментальным понятиям симметрии относятся плоскость симметрии, ось симметрии, центр симметрии. Плоскостью симметрии называется такая плоскость, которая делит фигуру на две зеркально равные части, расположенные друг относительно друга так, как предмет и его зеркальное отражение. Принцип "симметрии" широко используется в искусстве. Бордюры в архитектурных и скульптурных произведениях, орнаменты в прикладном искусстве, - все это примеры использования симметрии. Принцип симметрии очень часто используется совместно с принципом "золотого сечения". Таким примером может служить картина Рафаэля "Обручение Марии"

Геометрия орнаментов, бордюров, паркетов. Орнаментальное искусство одно из самых древних. С орнаментами мы встречаемся повсюду: в декоративно-прикладном искусстве, в росписях архитектурных сооружений, в чугунных решётках, окаймляющих сады, парки, дворцы. Орнамент – это узор, состоящий из повторяющихся, ритмически упорядоченных элементов. Орнамент, как правило, подчёркивает своим построением и формой архитектурные и конструктивные особенности предмета, природную красоту материала. В построении орнамента используют главным образом принцип симметрии.

Симметрия в архитектуре. Симметрия…является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство. Г.Вейль 

Театральная площадь, Большой театр О.Бове, А.Михайлов 1821-1853

Триумфальная арка Ж.Ф.Т.Шальгрен 1806-1836 Франция, Париж

Золотое сечение - (золотая пропорция, деление в крайнем и среднем отношении) — деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине. Отношение большей части к меньшей в этой пропорции выражается квадратичной иррациональностью φ=( √5+1)/2≈1,6180339887… и, наоборот, отношение меньшей части к большей 1/ φ = =( √5-1)/2≈0,6180339887…

Золотое сечение в искусстве «Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением и если первое можно сравнить с мерой золота, то второе – с драгоценным камнем». Иоганн Кеплер

Известно, что Сергей Эйзенштейн искусственно построил фильм «Броненосец Потёмкин» по правилам золотого сечения. Он разбил ленту на пять частей. В первых трёх действие развивается на корабле. В двух последних — в Одессе, где разворачивается восстание. Этот переход в город происходит точно в точке золотого сечения. Да и в каждой части есть свой перелом, происходящий по закону золотого сечения. В кадре, сцене, эпизоде происходит некий скачок в развитии темы: сюжета, настроения. Эйзенштейн считал, что, так как такой переход близок к точке золотого сечения, он воспринимается как наиболее закономерный и естественный.

Математика и музыка. Изучая высоту звука с помощью монохорда – простейшего инструмента Древних греков, Пифагор обнаружил поразительные вещи. Выяснилось, что приятные слуху созвучия – консонансы получаются лишь в том случае, когда длины струн, издающих эти звуки, соотносятся как целые числа первой четвёрки, т.е. 1:2, 2:3, 3:4. Это открытие потрясло Пифагора: оказалось, что звук и созвучие могут быть представлены простыми числами

Великий немецкий композитор XVII века Иоганн Себастьян Бах писал церковную музыку. Позднее уже после его смерти музыканты-исследователи выяснили, что многие мелодии композитора имеют цифровые коды - символы, а произведения точно математически просчитаны.

Французский композитор и музыкальный теоретик Жан Филипп Рамо в своём «Трактате о гармонии», написанном в 1722 году, говорил о том, что «музыка подчинена арифметике», уделял много внимания физико-математическим исследованиям.

Игорь Стравинский, хорошо знавший музыку мастеров эпохи Ренессанса, также находил много общего между математикой и музыкой. «Способ композиторского мышления – способ, которым я мыслю, - мне кажется, не очень отличается от математического», «музыкальная форма математична хотя бы потому, что она идеальна» - эти высказывания Стравинского ярко выражают его убеждения

Математика и литература "Математик, который не есть отчасти поэт,  не будет никогда подлинным математиком" К. Вейерштрасс

Некоторые ошибочно думают - говорила великий русский математик-женщина С. Ковалевская, что математика - это сухая наука. Они смешивают математику с арифметикой, в которой проводятся вычисления, порой трудные и скучные, с числами. Но для того чтобы быть настоящим математиком, добавила С.Ковалевская, нужно быть поэтом в душе.

Поэтами были многие восточные ученые-энциклопедисты средневековья. Достаточно упомянуть лишь таких крупных мусульманских ученых, как Ибн Сина (Авиценна) (X-XI в.), аль-Хайям (XI в.), аль-Беруни (XII в.), Ибн аль-Ясмин (XII в.), Ибн аль-Хаим (XV в.) и Ибн Гази (XV в.). Они сделали много в науке вообще и в математике особенно. Ибн Сина (Авиценна) Омар Хайям Аль-Беруни

Число 12 олицетворяет, в первую очередь, время: 12 часов (ноль часов) - начало новой эпохи, когда из бури и хаоса возникает новый мир. Так же 12 - это число солдат революции, и, невольно напрашивается ассоциация с двенадцатью апостолами новой, еще непонятной веры. Раскрытию авторской идеи способствует и структура поэмы. Она состоит из 12 глав, а число строк в поэме кратно 12...

Льюис Кэрролл (настоящее имя – Чарлз Латуидж Доджсон). Научные работы Кэрролла предвосхитили некоторые идеи математической логики. Но больше он известен как автор популярных повестей для детей. Так  в 1865 году он издал сказку «Алиса в стране чудес». Королева Англии, прочитав книгу, пришла в восторг от сказки и приказала срочно приобрести остальные сочинения Кэрролла. И очень удивилась, когда выяснилось, что все остальные произведения Кэрролла - сочинения по высшей математике, сравнительной анатомии, палеонтологии и систематике животных.

Никто не замечал, что в самом заглавии романа – «Война и мир» - закодирован закон золотого сечения. В самом деле, название романа построено на первых четырех членах ряда Фибоначчи 1, 2, 3, 5.Один союз, два существительных, три слова. Пять букв в первом ключевом. Отношение ключевых слов 5:3=1,666… есть первое рациональное приближение коэффициента золотого сечения.

Математика и живопись «И, поистине, живопись – это наука и законная дочь природы, ибо она порождена природой…» Леонардо да Винчи

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: “Пусть никто, не будучи математиком, не дерзнет читать мои труды”. Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в.

Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Вся фигура и картина в целом опутана здесь двумя золотыми треугольниками и сетью больших, средних и малых золотых прямоугольников, ориентированных по ширине или высоте полотна.

Наука и искусство, словно нити холста, переплетались в полотнах мастеров Возрождения. Живопись переходила в начертательную геометрию, а геометрия – в искусство.

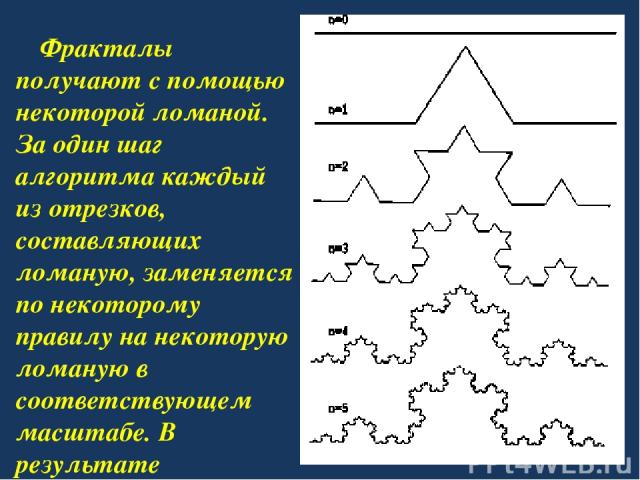
Фракталы. Люди придумали цифры и действия с ними, а потом в них же открыли множество законов, правил и теорем. Кроме того, оказалось, что в жизни цифр, линий, углов и бесконечно малых величин можно увидеть много красивого – изящные теоремы, тела, поверхности, даже условия задач. Числа живут своей жизнью, и мы, соприкоснувшись с ней, удивляемся, а иногда и любуемся ею. Компьютер дает нам возможность видеть на экране те или иные процессы, которые мы программируем.

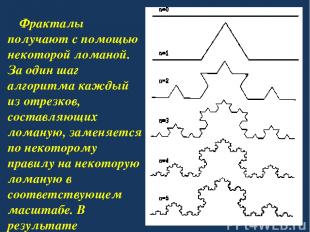
Фракталы получают с помощью некоторой ломаной. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется по некоторому правилу на некоторую ломаную в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

Очень часто описанным способом пользуются при рисовании орнаментов, облаков, деревьев и т. д.

Заключение: Примеры взаимопроникновения математики в различные сферы искусства и наоборот можно приводить бесконечно…И чем дальше этим занимаешься, тем увлекательнее становится такая работа. Но даже приведенных примеров, я думаю, достаточно для того, чтобы согласиться со словами Бертрана Рассела: «Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства».

Список литературы: 1. сайт: http://actual-art.ru 2. сайт: http://www.goldenmuseum.com/index_rus.html 3. А.И.Азевич «Двадцать уроков гармонии» библиотека журнала «Математика в школе», выпуск 7. Москва «Школа-Пресс», 1998год 4. А.В. Волошинов «Математика и искусство», Москва, «Просвещение»,1992 ГОД 5. Соколов А. Тайны золотого сечения. Техника – молодежи, 1978, № 5, с. 40 6. И.Ф.Шарыгин, Л.Н. Ерганжиева «Наглядная геометрия 5-6 классы» Москва, Издательский дом «Дрофа», 1998 год.. 7. Юшкевич А.П.Математика в ее истории. М. Янус. ИИЕТ РАН.1996

Спасибо за внимание!