Презентация на тему: Четырехугольники. Свойства четырехугольников. Решение задач

Четырехугольники. Свойства четырехугольников. Решение задач ГБОУ гимназия г. Сызрани Самарской области Автор: Константинова Ирина Альбертовна, учитель математики 261-106-202 2012 год

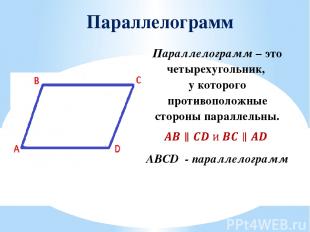
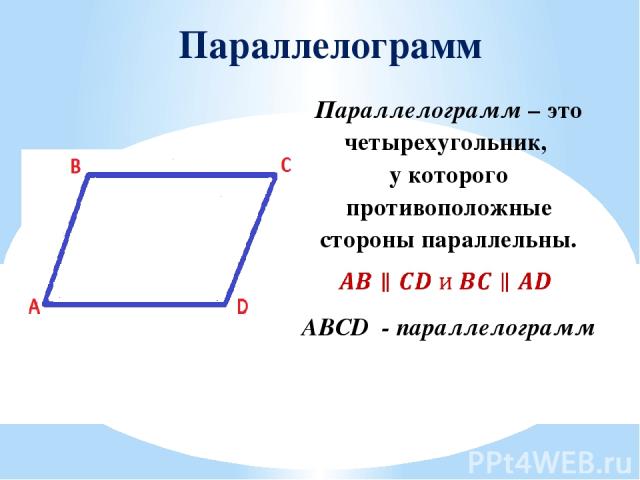
Параллелограмм ABCD - параллелограмм Параллелограмм–это четырехугольник, у которого противоположные стороны параллельны.

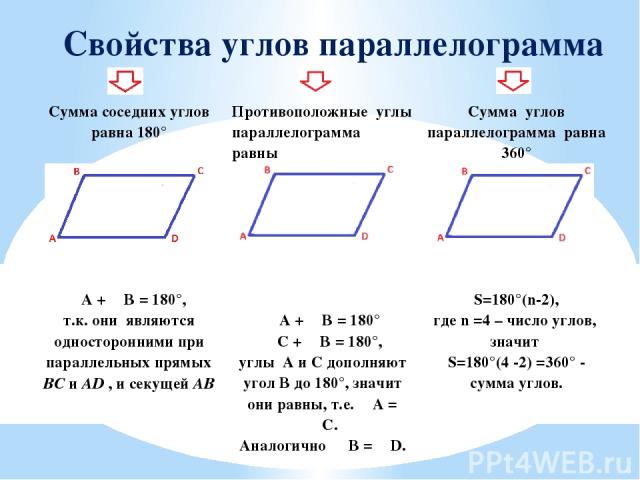
Свойства углов параллелограмма Сумма соседних углов равна 180° ∠A +∠B =180°, т.к. они являются односторонними при параллельных прямыхBCиAD, и секущейAB Противоположныеуглы параллелограмма равны ∠A +∠B = 180° ∠C +∠B = 180°, углыAиCдополняют уголBдо 180°, значит они равны, т.е.∠A = ∠С. Аналогично∠B = ∠D. Суммауглов параллелограмма равна 360° S=180°(n-2), гдеn=4 – число углов,значит S=180°(4-2)=360° - сумма углов.

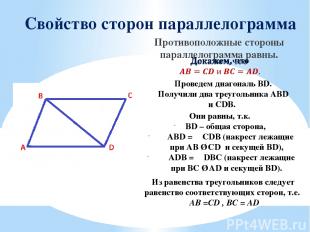
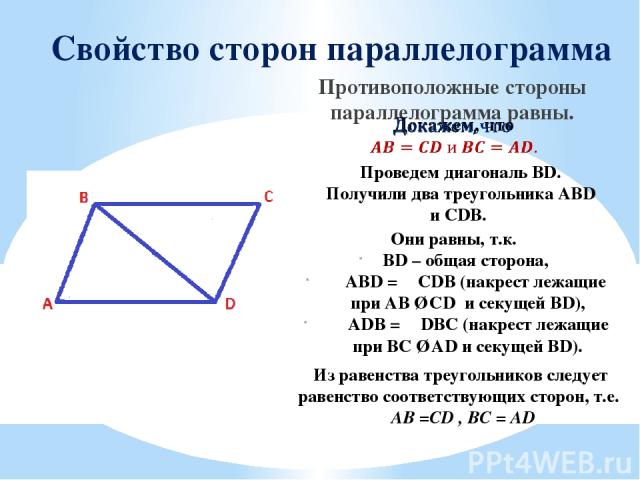
Свойство сторон параллелограмма Противоположные стороны параллелограмма равны. Проведем диагональ BD. Получили два треугольника АВD и СDB. Они равны, т.к. BD – общая сторона, ∠ABD = ∠CDB (накрест лежащие при AB ∥ CD и секущей BD), ∠ADB = ∠DBC (накрест лежащие при BС ∥ AD и секущей BD). Из равенства треугольников следует равенство соответствующих сторон, т.е. AB =CD , BC = AD

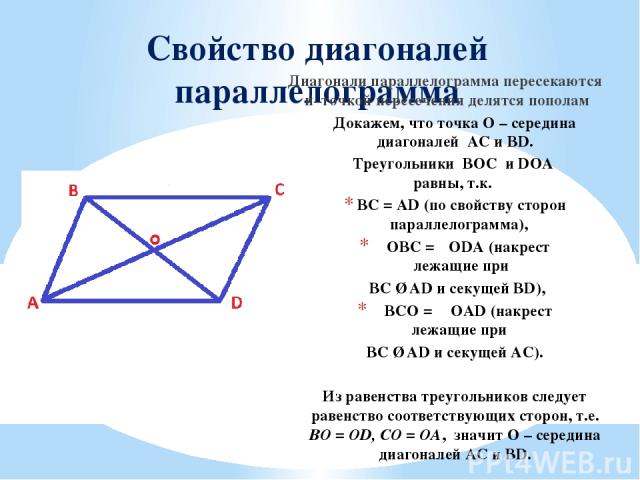
Свойство диагоналей параллелограмма Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам Докажем, что точка О – середина диагоналей AC и BD. Треугольники BOC и DOA равны, т.к. BC = AD (по свойству сторон параллелограмма), ∠OBC =∠ODA (накрест лежащие при BC ∥ AD и секущей BD), ∠BCO = ∠OAD (накрест лежащие при BC ∥ AD и секущей AC). Из равенства треугольников следует равенство соответствующих сторон, т.е. BO = OD, CO = OA, значит O – середина диагоналей AC и BD.

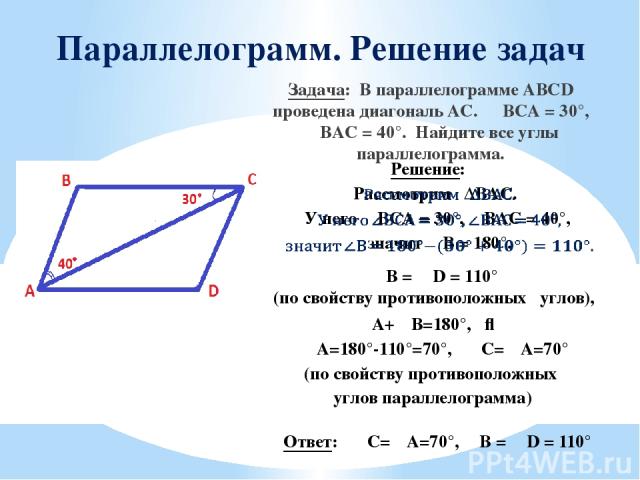
Параллелограмм. Решение задач Задача: В параллелограмме ABCD проведена диагональ AC. ∠BCA = 30°, ∠BAC = 40°. Найдите все углы параллелограмма. Решение: ∠B = ∠D = 110° (по свойству противоположных углов), ∠A+∠B=180°, ⇒ ∠A=180°-110°=70°, ∠C=∠A=70° (по свойству противоположных углов параллелограмма) Ответ: ∠C=∠A=70°, ∠B = ∠D = 110°

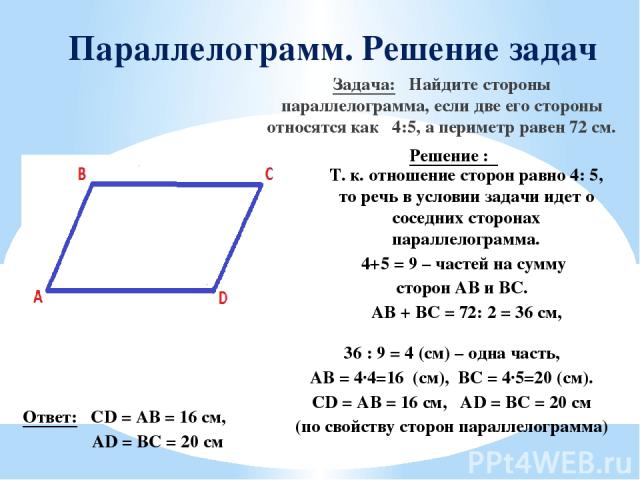
Параллелограмм. Решение задач Задача: Найдите стороны параллелограмма, если две его стороны относятся как 4:5, а периметр равен 72 см. Решение : Т. к. отношение сторон равно 4: 5, то речь в условии задачи идет о соседних сторонах параллелограмма. 4+5 = 9 – частей на сумму сторон AB и BC. AB + BC = 72: 2 = 36 см, 36 : 9 = 4 (см) – одна часть, AB = 4·4=16 (см), BC = 4·5=20 (см). CD = AB = 16 см, AD = BC = 20 см (по свойству сторон параллелограмма) Ответ: CD = AB = 16 см, AD = BC = 20 см

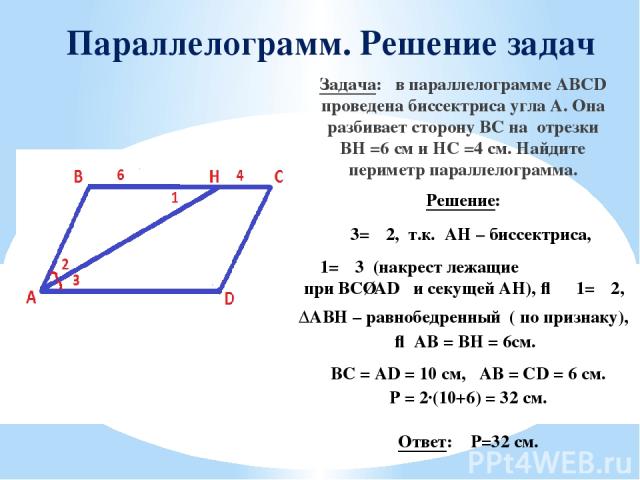
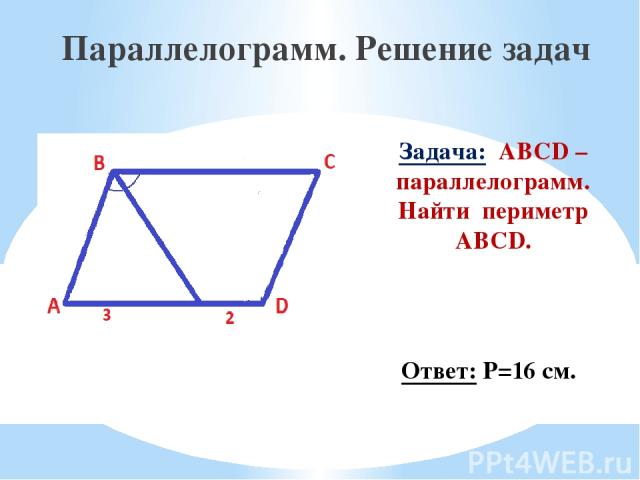
Параллелограмм. Решение задач Задача: в параллелограмме ABCD проведена биссектриса угла А. Она разбивает сторону ВС на отрезки BH =6 см и HC =4 см. Найдите периметр параллелограмма. Решение: ∠3=∠2, т.к. АH – биссектриса, ∠1=∠3 (накрест лежащие при BC∥AD и секущей AH), ⇒ ∠1=∠2, ΔABH – равнобедренный ( по признаку), ⇒ AB = BH = 6cм. BC = AD = 10 cм, AB = CD = 6 cм. Р = 2·(10+6) = 32 см. Ответ: P=32 см.

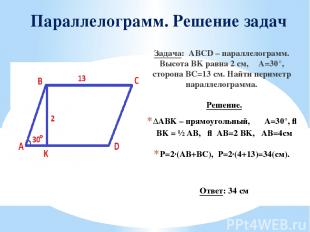
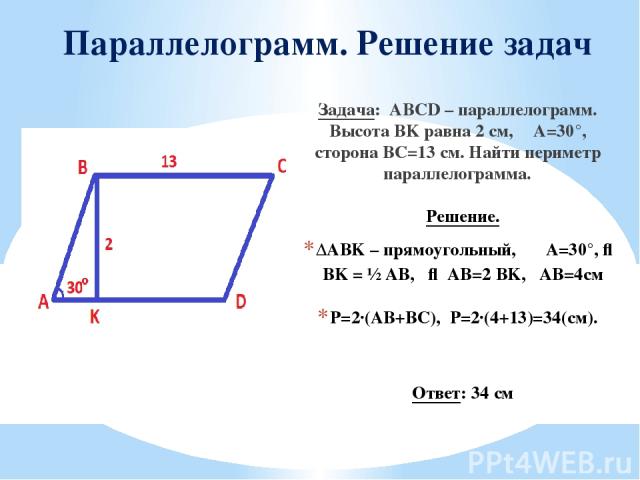
Параллелограмм. Решение задач Задача: ABCD – параллелограмм. Высота BK равна 2 см, ∠A=30°, сторона BC=13 см. Найти периметр параллелограмма. Решение. ΔABK – прямоугольный, ∠A=30°, ⇒ BK = ½ AB, ⇒ AB=2 BK, AB=4см P=2·(AB+BC), Р=2·(4+13)=34(см). Ответ: 34 см

Решение задач по готовым чертежам с последующей самопроверкой

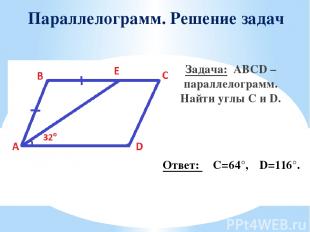
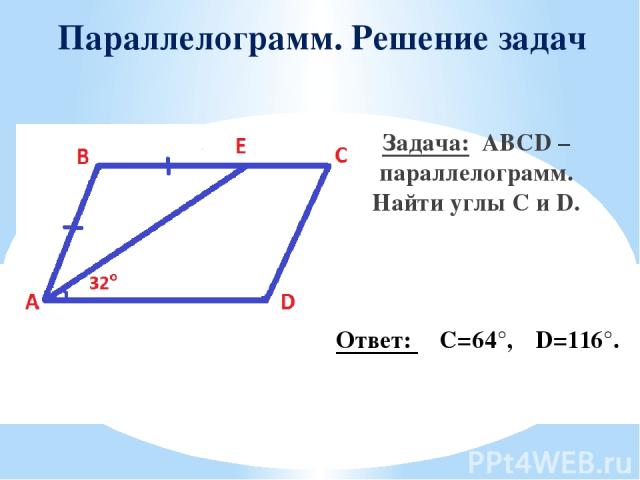
Параллелограмм. Решение задач Задача: ABCD – параллелограмм. Найти углы C и D. Ответ: ∠C=64°,∠D=116°.

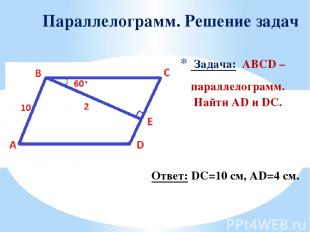
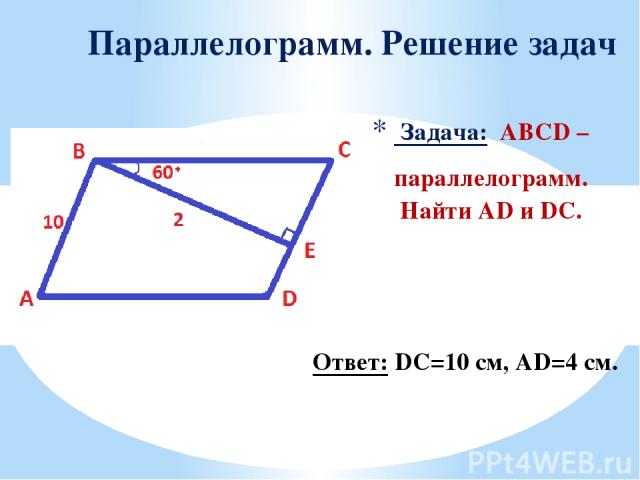
Задача: ABCD – параллелограмм. Найти AD и DC. Параллелограмм. Решение задач Ответ: DC=10 см, AD=4 см.

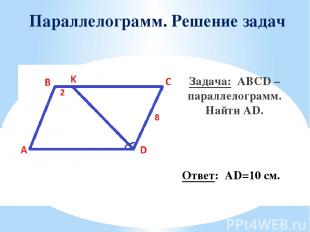
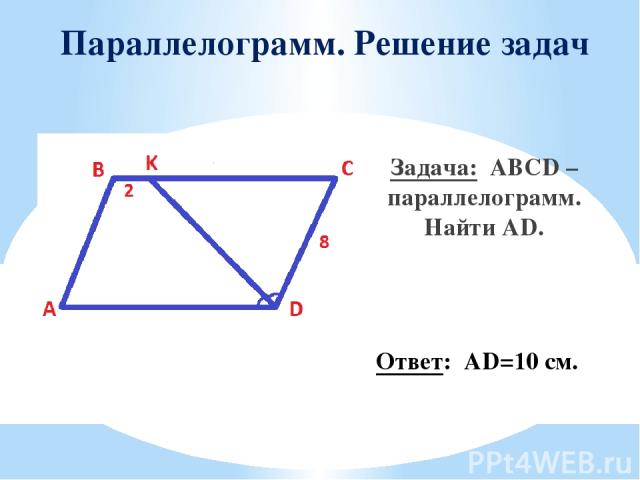
Параллелограмм. Решение задач Задача: ABCD – параллелограмм. Найти AD. Ответ: AD=10 см.

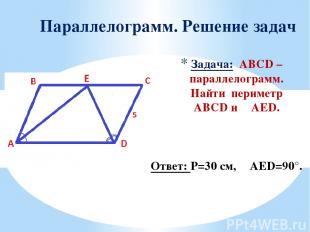
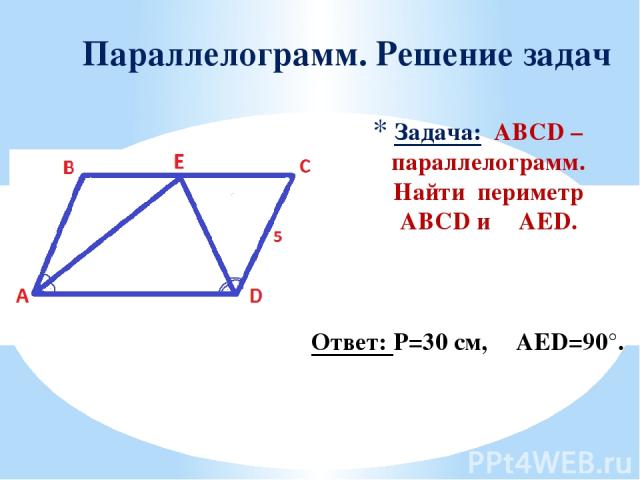
Задача: ABCD – параллелограмм. Найти периметр ABCD и ∠AED. Параллелограмм. Решение задач Ответ: Р=30 см, ∠AED=90°.

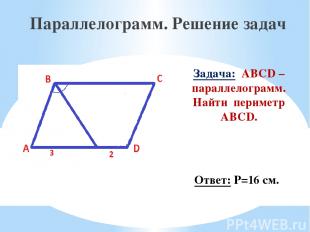
Задача: ABCD – параллелограмм. Найти периметр ABCD. Параллелограмм. Решение задач Ответ: Р=16 см.

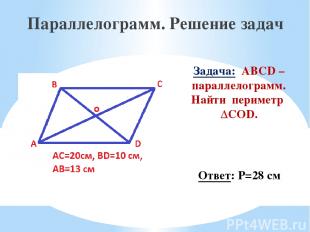
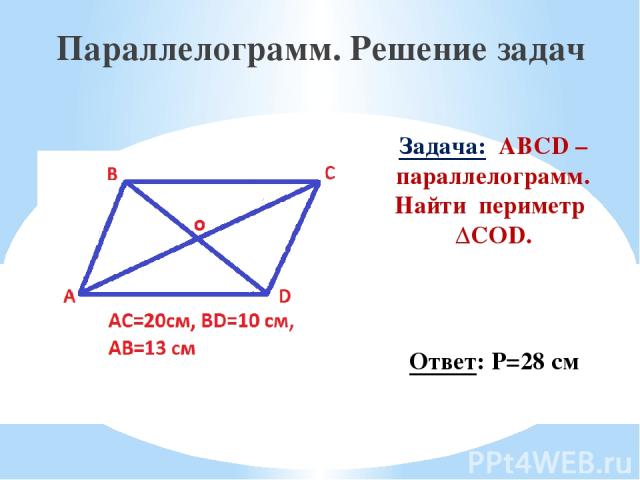
Задача: ABCD – параллелограмм. Найти периметр ΔCOD. Параллелограмм. Решение задач Ответ: Р=28 см

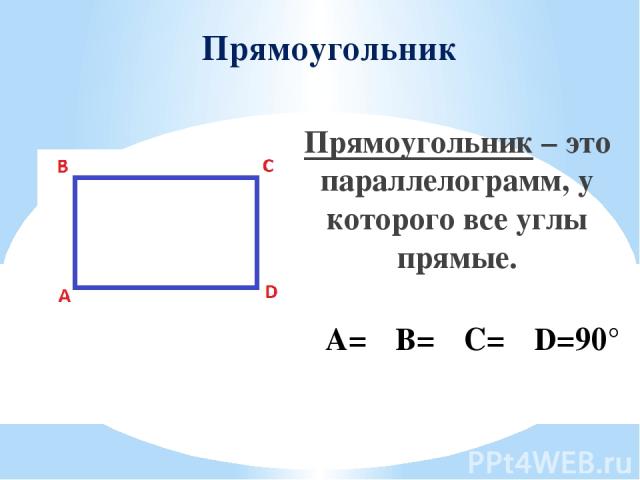
Прямоугольник Прямоугольник – это параллелограмм, у которого все углы прямые. ∠A=∠B=∠C=∠D=90°

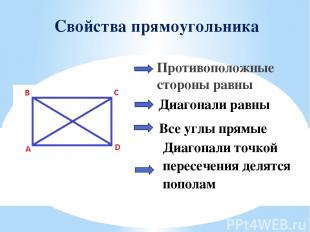
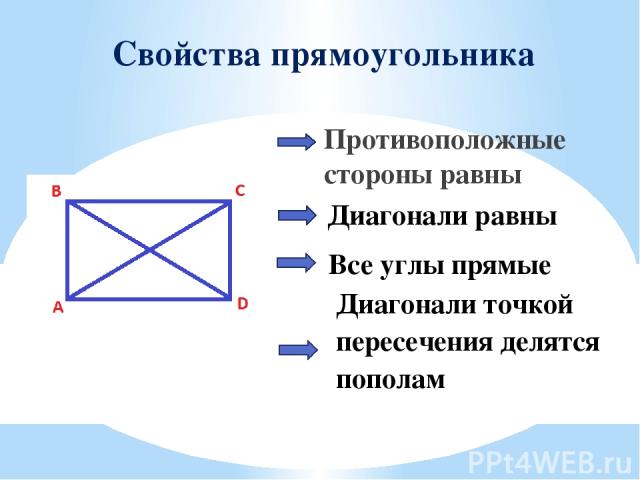
Свойства прямоугольника Противоположные стороны равны Все углы прямые Диагонали равны Диагонали точкой пересечения делятся пополам

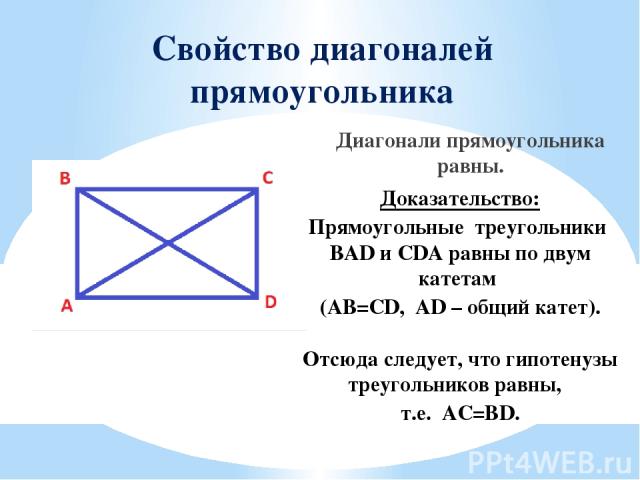
Свойство диагоналей прямоугольника Диагонали прямоугольника равны. Доказательство: Прямоугольные треугольники BAD и CDA равны по двум катетам (AB=CD, AD – общий катет). Отсюда следует, что гипотенузы треугольников равны, т.е. AC=BD.

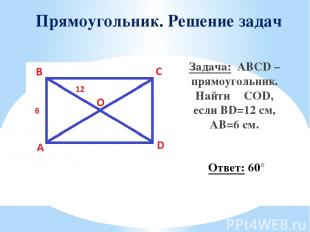
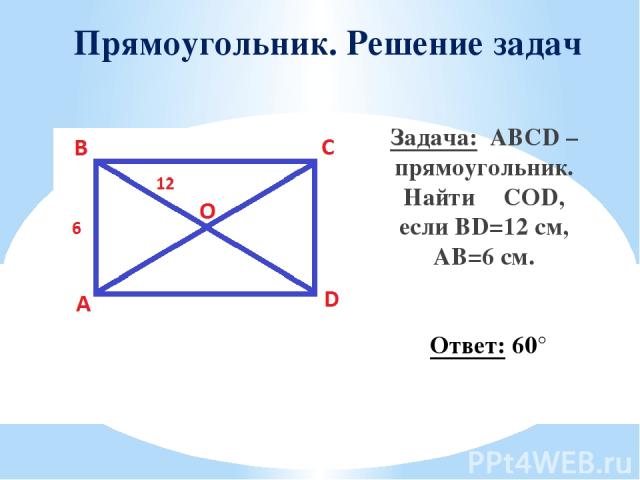
Прямоугольник. Решение задач Задача: ABCD – прямоугольник. Найти ∠COD, если BD=12 см, AB=6 см. Ответ: 60°

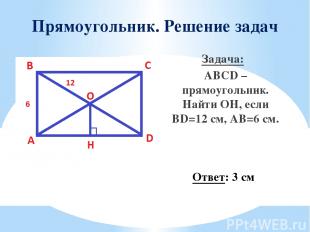
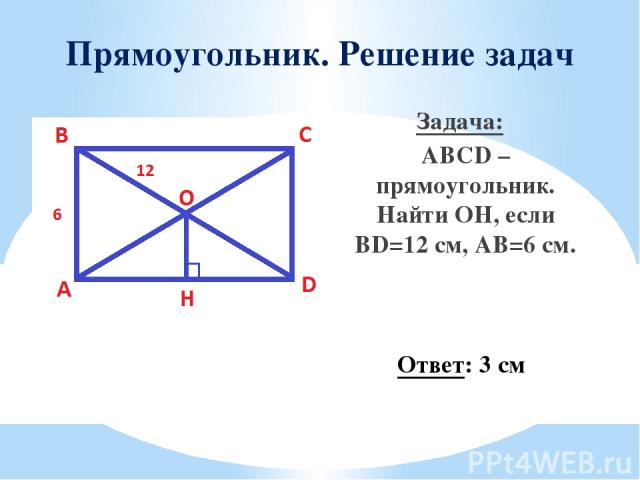
Прямоугольник. Решение задач Задача: ABCD – прямоугольник. Найти OН, если BD=12 см, AB=6 см. Ответ: 3 см

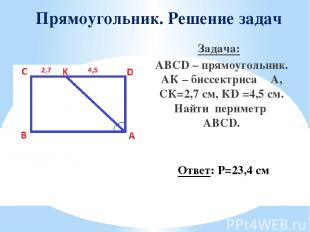
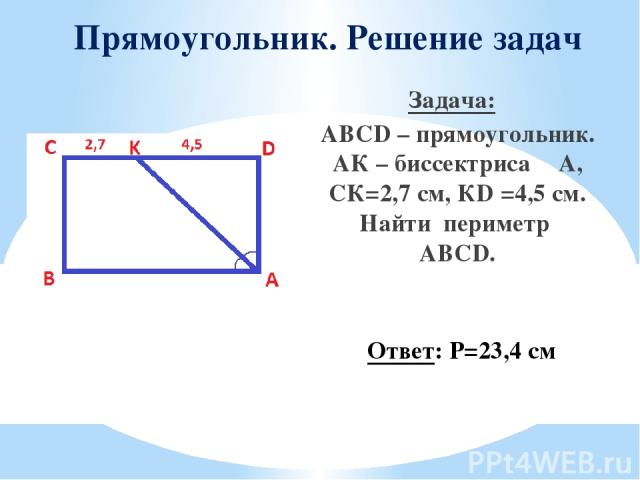
Прямоугольник. Решение задач Задача: ABCD – прямоугольник. АК – биссектриса ∠A, СК=2,7 см, КD =4,5 см. Найти периметр ABCD. Ответ: Р=23,4 см

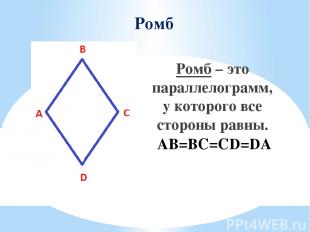
Ромб Ромб – это параллелограмм, у которого все стороны равны. AB=BC=CD=DA

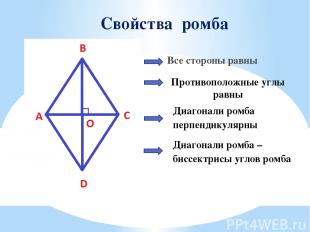
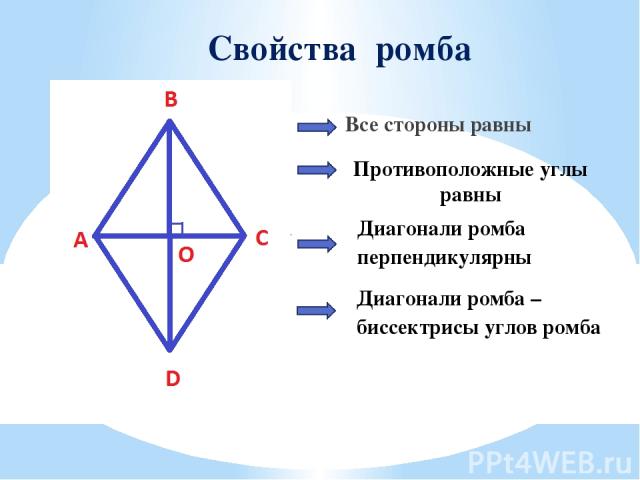
Свойства ромба Все стороны равны Противоположные углы равны Диагонали ромба перпендикулярны Диагонали ромба – биссектрисы углов ромба

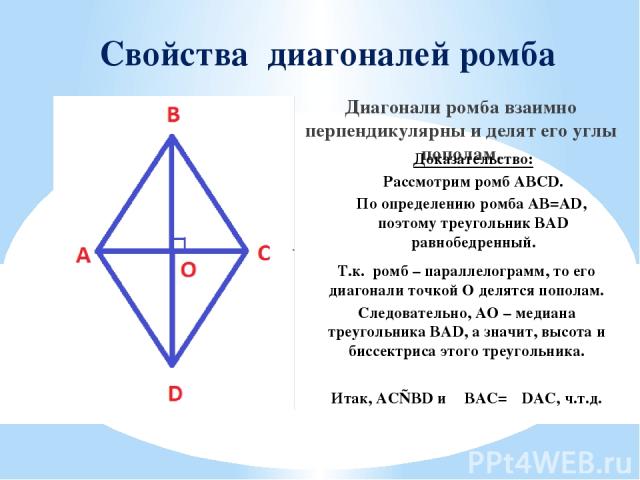
Свойства диагоналей ромба Диагонали ромба взаимно перпендикулярны и делят его углы пополам. Доказательство: Рассмотрим ромб ABCD. По определению ромба AB=AD, поэтому треугольник BAD равнобедренный. Т.к. ромб – параллелограмм, то его диагонали точкой О делятся пополам. Следовательно, АО – медиана треугольника BAD, а значит, высота и биссектриса этого треугольника. Итак, AC⊥BD и ∠BAC=∠DAC, ч.т.д.

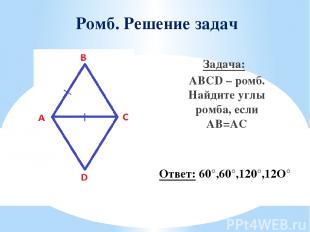
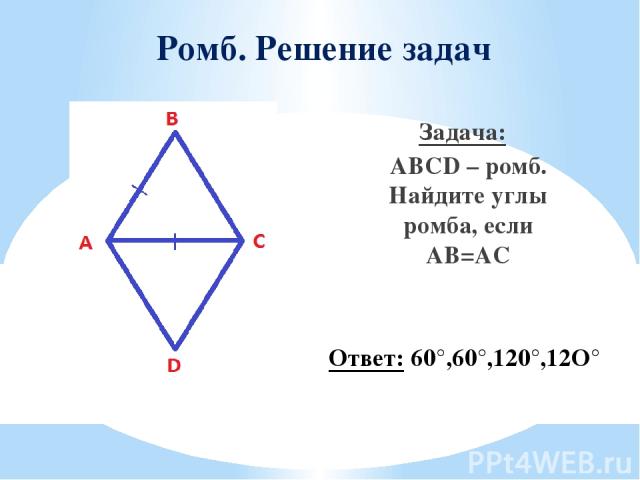
Ромб. Решение задач Задача: ABCD – ромб. Найдите углы ромба, если AB=AC Ответ: 60°,60°,120°,12O°

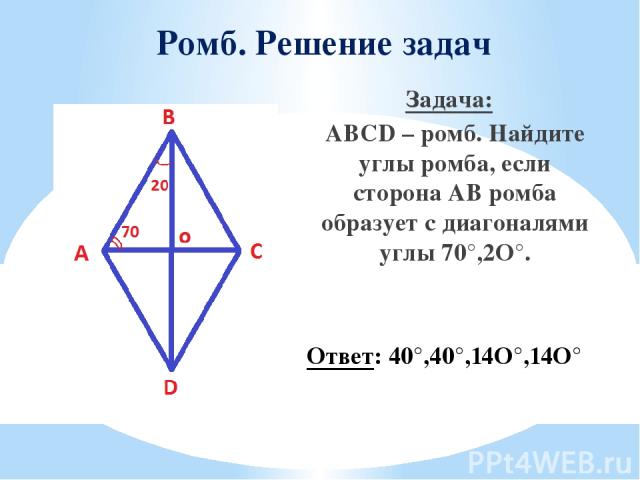
Ромб. Решение задач Задача: ABCD – ромб. Найдите углы ромба, если сторона АВ ромба образует с диагоналями углы 70°,2O°. Ответ: 40°,40°,14O°,14O°

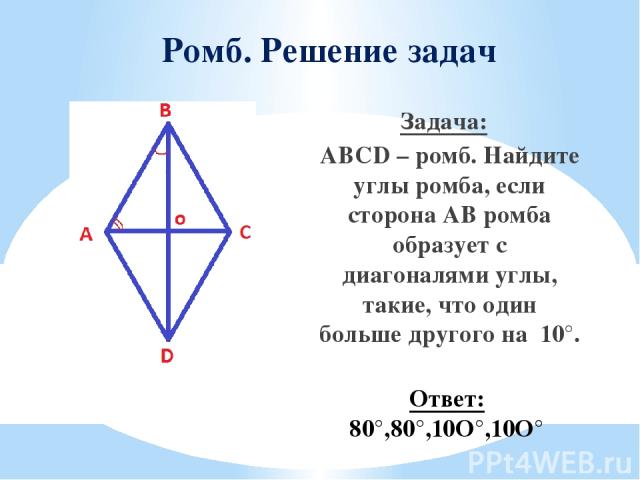
Ромб. Решение задач Задача: ABCD – ромб. Найдите углы ромба, если сторона АВ ромба образует с диагоналями углы, такие, что один больше другого на 10°. Ответ: 80°,80°,10O°,10O°

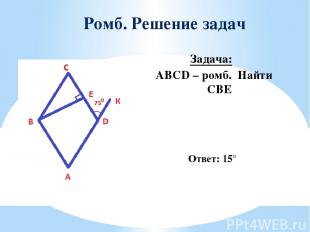
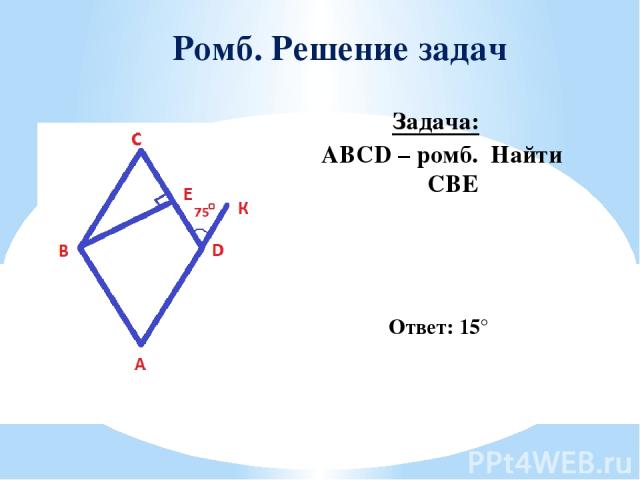
Ромб. Решение задач Задача: ABCD – ромб. Найти ∠CBE Ответ: 15°

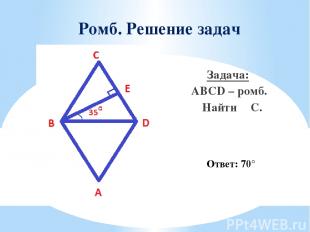
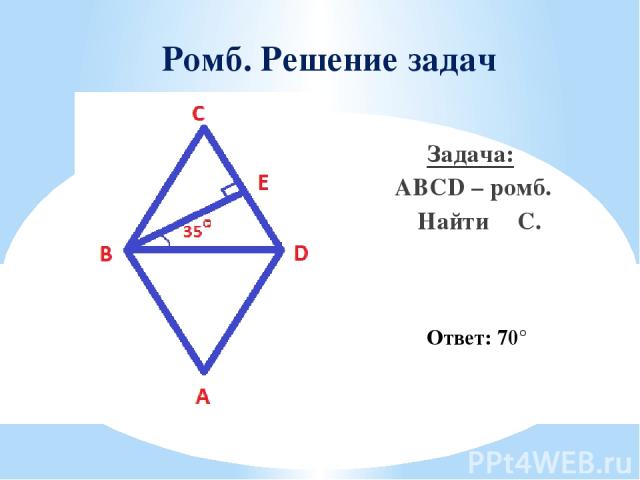
Ромб. Решение задач Задача: ABCD – ромб. Найти ∠С. Ответ: 70°

Квадрат Квадрат – это прямоугольник, у которого все стороны равны. AB = BC = CD = DA

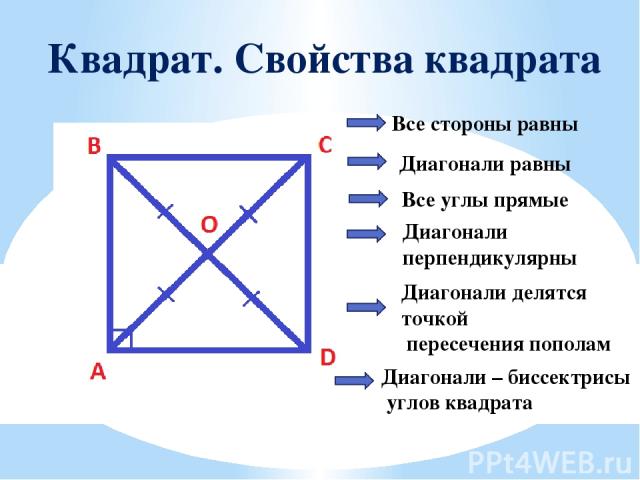
Квадрат. Свойства квадрата Все стороны равны Диагонали равны Все углы прямые Диагонали перпендикулярны Диагонали делятся точкой пересечения пополам Диагонали – биссектрисы углов квадрата

Литература Л.С. Атанасян «Геометрия. 7-9 классы» Гаврилова Н.Ф. Поурочные разработки по геометрии, 8 класс Н.Б. Мельникова «Контрольные работы по геометрии» Л.С. Атанасян «Дидактические материалы по геометрии 8 класс»