Презентация на тему: Арифметические действия в двоичной системе счисления

«АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯВ ДВОИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ»

ЗАДАНИЕ «ТЕЗИСЫ» Верно ли каждое из следующих утверждений?Если «Да», то записывайте 1.Если «Нет», то записывайте 0.В результате должно получиться двоичное число.

ТЕЗИСЫ Число 10, записанное в десятичной системе счисления, меньше числа 10, записанного в восьмеричной системе счисления. Число 10, записанное в десятичной системе счисления, в двоичной системе счисления записывается как 1011 Число А21СFD4 записано в шестнадцатиричной системе счисления. В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе.

Полученное двоичное число переведите в десятичную, восьмеричную и шестнадцатиричную системы счисления.

ТЕЗИСЫ Число 10, записанное в десятичной системе счисления, меньше числа 10, записанного в восьмеричной системе счисления. Число 6398 записано в восьмеричной системе счисления. Число 3005,234 записано с ошибкой. Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

10101000102 = 67410 10101000102 = 1242810101000102 = 2А216

Пьер Симон Лаплас о своем отношении к двоичной (бинарной) системе счисления «В своей бинарной арифметике Лейбниц видел прообраз творения. Ему представлялось, что единица представляет божественное начало, а нуль – небытие и что высшее существо создает все из небытия точно таким же образом, как единица и нуль в его системе выражают все числа…». «Мысль – выражать все числа немногими знаками, придавая им значение по форме, её значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна …» Пьер Симон Лапласфранцузский астроном, математик и физик (1749 – 1827 гг.) Эти слова подчеркивают универсальность алфавита, состоящего из двух символов.

Все позиционные системы счисления «одинаковы», а именно, во всех них выполняются арифметические операции по одним и тем же правилам: справедливы одни и те же законы арифметики:-коммутативный (переместительный) m + n = n + m m · n = n · m ассоциативный (сочетательный) ( m + n ) + k = m + ( n +  k ) = m + n + k (m · n ) · k = m · ( n ·  k ) = m · n · k дистрибутивный (распределительный) ( m + n ) · k = m ·  k + n ·  k справедливы правила сложения, вычитания, умножения и деления столбиком; правила выполнения арифметических операций опираются на таблицы сложения и умножения.

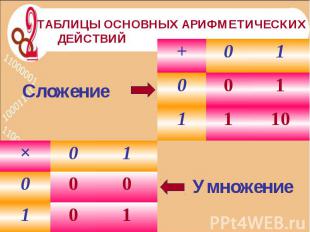
Таблицы основных арифметических действий Сложение Умножение

Домашнее задание 1) Выучить правила выполнения арифметических действий в двоичной системе счисления, выучить таблицы сложения, вычитания, умножения. 2) Выполнить задания:

рефлексия : - ) - радостное лицо: - ( - грустное лицо; - ) - подмигивающая улыбка: 0 ) - клоун8:-) - маленькая девочка

Если вы считаете, что хорошо поработали, справились с заданием и урок вам понравился, то нарисуйте улыбающийся смайликЕсли вы довольны результатами вашей работы, но урок вам не понравился, то нарисуйтеЕсли урок вам понравился, но вы не успели справиться со всеми заданиями, то нарисуйтеЕсли урок вам не понравился и вы недовольны результатами своей работы на уроке, то нарисуйте