Презентация на тему: Системы счисления: история, назначение, применение

Введение. Введение. Виды систем счисления. История развития информационных систем. Представление чисел, а также информации в ЭВМ. Арифметические операции в позиционных СС. Применение систем счисления.

«Все есть число» - так говорили древние мудрецы, подчеркивая важнейшую роль чисел в нашей жизни. «Все есть число» - так говорили древние мудрецы, подчеркивая важнейшую роль чисел в нашей жизни. Люди всегда пользовались числами, считали и записывали, даже пять тысяч лет назад люди уже знали числа. Но в любом случае каждое число изображалось с помощью определенных символов – цифр.

Цифры - это символы, участвующие в записи числа. Цифры - это символы, участвующие в записи числа. А что же тогда число? Число – это некоторая величина, которая складывается из цифр по особым правилам. В разные времена и у разных народов эти правила были различны и сегодня их называют СИСТЕМАМИ СЧИСЛЕНИЯ.

Системы счисления: Системы счисления: -позиционные -непозиционные Непозиционной называется такая СС, у которой вес цифры не зависит от ее местоположения в записи числа. Непозиционные СС появились раньше позиционных и имеют долгую историю развития.

1) В древние времена, когда люди начали считать, появилась потребность в записи чисел. Количество предметов изображалось с помощью черточек или засечек на какой-либо твердой поверхности. Ученые назвали этот способ записи чисел единичной или унарной системой счисления. 1) В древние времена, когда люди начали считать, появилась потребность в записи чисел. Количество предметов изображалось с помощью черточек или засечек на какой-либо твердой поверхности. Ученые назвали этот способ записи чисел единичной или унарной системой счисления.

2)Древнеегипетская десятичная СС. 2)Древнеегипетская десятичная СС. Данная СС возникла во второй половине третьего тысячелетия до н.э. Вместо цифр использовались специальные иероглифы. Именно из комбинации таких «цифр» записывались все числа и каждая «цифра» повторялась не более девяти раз:

Все числа составлялись из ключевых иероглифов при помощи обычного сложения. Все числа составлялись из ключевых иероглифов при помощи обычного сложения. Умножение и деление производили путем последовательного удвоения чисел. Дроби в Египте тоже существовали и все они имели в числителе единицу (кроме числа 2/3)

3) Римская СС. 3) Римская СС. Данная СС не намного отличается от египетской СС, здесь только используются совершенно другие обозначения чисел: I – 1 C - 100 V - 5 D - 500 X - 10 M - 1000 L - 50

Римская СС подразделялась также на греческую СС. Правила этих СС были одинаковы, а обозначения различались: Римская СС подразделялась также на греческую СС. Правила этих СС были одинаковы, а обозначения различались: Г – пять Н - сто Δ – десять Х - тысяча М – десять тысяч

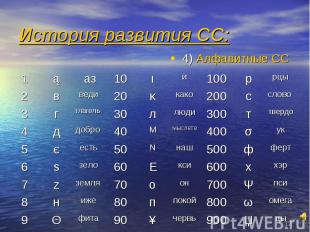
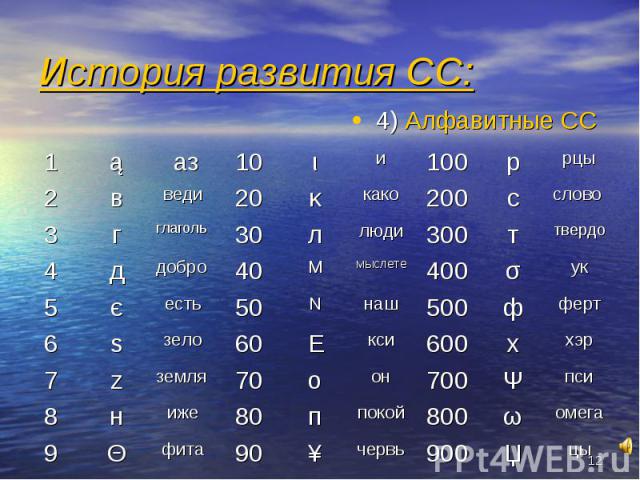
4) Алфавитные СС 4) Алфавитные СС

Данная таблица – пример написания цифр наиболее совершенной непозиционной СС, которой пользовались греки, финикийцы и славяне. Алфавитная система была принята и в Древней Руси. До конца 17 века люди использовали 27 букв кириллицы как цифры. Данная таблица – пример написания цифр наиболее совершенной непозиционной СС, которой пользовались греки, финикийцы и славяне. Алфавитная система была принята и в Древней Руси. До конца 17 века люди использовали 27 букв кириллицы как цифры.

Казалось бы, что непозиционные СС не совсем удобны. Но наши предки умели и записывали числа , равные 1000, 100000 и даже миллиону. Так, например, числа 1000, 2000, 3000… записывали теми же цифрами, что и 1, 2, 3… , только перед цифрой ставили слева снизу специальный знак - титла. Число 10000 обозначалось той же буквой, что и 1, только эту букву обводили кружком(это число называлось «тьма»). Число 100000 называли «легион», 10 легионов – «леорд». Самая большая из величин, имеющих свое обозначение, называлась «колода», она равнялась 1050. Считалось, что «боле сего несть человеческому уму разумевати» . Казалось бы, что непозиционные СС не совсем удобны. Но наши предки умели и записывали числа , равные 1000, 100000 и даже миллиону. Так, например, числа 1000, 2000, 3000… записывали теми же цифрами, что и 1, 2, 3… , только перед цифрой ставили слева снизу специальный знак - титла. Число 10000 обозначалось той же буквой, что и 1, только эту букву обводили кружком(это число называлось «тьма»). Число 100000 называли «легион», 10 легионов – «леорд». Самая большая из величин, имеющих свое обозначение, называлась «колода», она равнялась 1050. Считалось, что «боле сего несть человеческому уму разумевати» .

Так как запись чисел с помощью алфавитной СС была достаточно сложна, то в старину на Руси среди простого народа широко применялись СС, отдаленно напоминающие римскую. С их помощью сборщики податей заполняли квитанции об уплате подати – ясака и делали записи в податной тетради. Числа обозначали с помощью специальных символов: Так как запись чисел с помощью алфавитной СС была достаточно сложна, то в старину на Руси среди простого народа широко применялись СС, отдаленно напоминающие римскую. С их помощью сборщики податей заполняли квитанции об уплате подати – ясака и делали записи в податной тетради. Числа обозначали с помощью специальных символов:

Алфавитные СС были мало пригодны для оперирования с большими числами. В ходе развития человеческого общества эти системы уступили место позиционным системам. Алфавитные СС были мало пригодны для оперирования с большими числами. В ходе развития человеческого общества эти системы уступили место позиционным системам. Позиционная СС – это такая СС, в которой вес цифры (количественный эквивалент) зависит от ее местоположения в записи числа. ( Например, число 222. В его записи используется трижды цифра 2, однако вклад каждой цифры в величину числа разный. Первая 2 – это число сотен, вторая – число десятков, третья – число единиц. Эти цифры различаются и по весу. В непозиционных СС такой принцип разделения отсутствует.)

Позиционных СС также несколько, но наиболее древние из них Вавилонская и Индийская мультипликативная системы. Позиционных СС также несколько, но наиболее древние из них Вавилонская и Индийская мультипликативная системы. Например, пусть десятки обозначаются символом X, тогда сотни – Y. Число 323 будет выглядеть так: 3Y2X3. Для записи одинакового числа единиц, десяток, сотен применяются одни и те же символы, но после каждого символа пишется название соответствующего разряда. По такому принципу работают упомянутые выше СС.

Наиболее важным открытием является нуль. Еще греческие астрономы использовали его для обозначения нулевого разряда ( ouden (греч) – ничто). Индийцы переняли нуль у греков и постепенно создали десятичную СС , которой мы пользуемся и по сей день. Ее в Европу завезли из Индии арабы, поэтому данная СС называется арабской. Наиболее важным открытием является нуль. Еще греческие астрономы использовали его для обозначения нулевого разряда ( ouden (греч) – ничто). Индийцы переняли нуль у греков и постепенно создали десятичную СС , которой мы пользуемся и по сей день. Ее в Европу завезли из Индии арабы, поэтому данная СС называется арабской.

простота выполнения арифметических операций. простота выполнения арифметических операций. ограниченное количество символов, необходимых для записи числа. Примеры позиционных СС:

все числовые данные хранятся в ЭВМ в двоичном виде, однако формы хранения целых и действительных чисел различны : все числовые данные хранятся в ЭВМ в двоичном виде, однако формы хранения целых и действительных чисел различны : целые числа хранятся в форме с фиксированной запятой. действительные числа хранятся в форме с плавающей запятой. Необходимость различного представления целых и действительных чисел вызвана тем, что скорость выполнения арифметических операций над числами с плавающей запятой существенно ниже скорости выполнения этих же операций над числами с фиксированной запятой.

Любой текст состоит из последовательности определенных символов (букв, знаков препинания и т.д.). Любой текст состоит из последовательности определенных символов (букв, знаков препинания и т.д.). Обратим особое внимание на символ «пробел» - хотя на экране и на бумаге пробел – пустое, свободное место, на клавиатуре ЭВМ ему соответствует специальная клавиша. Как и любая информация, текстовая информация хранится в ЭВМ в особом , закодированном (двоичном) виде.

Для этого каждому символу ставится в соответствие некоторое неотрицательное число, называемое кодом символа, и это число записывается в память ЭВМ в двоичном виде. Конкретное соответствие между символами и их кодами называется системой кодировки. В современных ЭВМ, как правило, используются 8-разрядные коды символов (реже – 16-разрядные).Использование данных кодов позволяет закодировать 256 различных символов, что вполне достаточно для практических нужд. При этом код символа занимает ровно 1 байт памяти. Для этого каждому символу ставится в соответствие некоторое неотрицательное число, называемое кодом символа, и это число записывается в память ЭВМ в двоичном виде. Конкретное соответствие между символами и их кодами называется системой кодировки. В современных ЭВМ, как правило, используются 8-разрядные коды символов (реже – 16-разрядные).Использование данных кодов позволяет закодировать 256 различных символов, что вполне достаточно для практических нужд. При этом код символа занимает ровно 1 байт памяти.

Мониторы современных ПК могут работать в двух режимах: текстовом и графическом. Мониторы современных ПК могут работать в двух режимах: текстовом и графическом. В текстовом режиме экран разбивается на 25 строк по 80 символов в строке. Данный режим предназначен для вывода на экран монитора текстов и простых рисунков. В графическом режиме экран разделяется на отдельные светящиеся точки – пиксели. Любое графическое изображение хранится в памяти в виде информации о каждом пикселе на экране. Состояние каждого пикселя описывается последовательностью нулей и единиц, соответствующих кодировке его цвета. Такую форму представления изображений называют растровой.

Развитие ЭВМ в последнее время позволяет записывать и воспроизводить на компьютерах музыку и человеческую речь. Существует 2 способа звукозаписи: Развитие ЭВМ в последнее время позволяет записывать и воспроизводить на компьютерах музыку и человеческую речь. Существует 2 способа звукозаписи: цифровая запись – реальные звуковые волны, которые преобразуются в цифровую информацию путем измерения звука тысячи раз в секунду. Этот процесс называется дискретизацией и возможен на компьютере, если на нем присутствует звуковая плата. Форматы звука: mp3, WAV и т.д. MIDI-запись – это не реальный звук, а запись определенных команд-указаний. MIDI-запись – электронный эквивалент нотной записи. Существуют также видео файлы – это сложный синтез звуковой дорожки и графических изображений.

Итак, мы выяснили, что в ЭВМ любая информация (графическая, текстовая и т.д.) кодируется и записывается с помощью всего двух цифр – нуля и единицы (двоичное кодирование). И над этими цифрами можно провести арифметические операции, такие как сложение и вычитание, умножение и деление. Рассмотрим это более подробно: Итак, мы выяснили, что в ЭВМ любая информация (графическая, текстовая и т.д.) кодируется и записывается с помощью всего двух цифр – нуля и единицы (двоичное кодирование). И над этими цифрами можно провести арифметические операции, такие как сложение и вычитание, умножение и деление. Рассмотрим это более подробно:

1) Перевод чисел из P-ичной СС в десятичную. 1) Перевод чисел из P-ичной СС в десятичную. Допустим, дано число в P-ичной СС. Требуется получить его запись в десятичной СС. Для этого представим данное число в развернутой форме a=a(n)*P(n)+a(n-1)*P(n-1)+…+a(1)*P+a(0) и воспользуемся алгоритмом решения данной задачи:

- каждая цифра числа в P-ичной СС переводится в число в десятичной СС. - каждая цифра числа в P-ичной СС переводится в число в десятичной СС. - полученные числа нумеруются справа налево начиная с нуля (номера соответствуют степеням P в многочлене) - десятичное число, соответствующее каждой P-ичной цифре, умножается на P(k), где k-номер этого числа из пункта 2,и результаты складываются, причем все эти арифметические действия проводятся в десятичной СС.

Примеры перевода чисел: Примеры перевода чисел: 1) Переведем 1001101(2) – двоичное число в A(10): 1001101(2)=2^0+2^2+2^3+2^6=77(10) 2) Переведем 2143(5) в A(10): 2143(5)=2*5^3+1*5^2+4*5+3=298(10) Задания: 1) Перевести из B0F9(16) в А(10). 2) Перевести из 1101(2) в А(10).

2) Сложение и вычитание. 2) Сложение и вычитание. Во всех традиционных СС эти арифметические операции выполняются по одним и тем же правилам (согласно специальным таблицам). В P-ичной СС таблица сложения – это результат сложения каждой цифры алфавита P-ичной СС с любой другой цифрой этой же СС. Достаточно простой таблицей является таблица сложения в двоичной СС: В шестнадцатеричной СС такая таблица во много раз массивней и больше.

Примеры сложения чисел: Примеры сложения чисел: 101,01(2) 21(3) – троичная СС + 1,11(2) + 2,1(3) ------------- -------- 111,00(2) 100,1(3) Задания: Сложите : 11010101(2) и 1110(2); 1234(5) и 4321(5).

Вычитание из большего числа меньшего в P-ичной СС тоже производится столбиком аналогично вычитанию в десятичной СС с использованием все той же таблицы сложения в P-ичной СС. Вычитание из большего числа меньшего в P-ичной СС тоже производится столбиком аналогично вычитанию в десятичной СС с использованием все той же таблицы сложения в P-ичной СС. Примеры вычитания: 101(2) 210(3) - 10,1(2) - 102(3) ------------ ----------- 10,1(2) 101(3) Задания: 4321(5) - 1234(5); 11010101(2) - 1110(2).

3) Умножение. 3) Умножение. Для выполнения умножения двух многозначных чисел в P-ичной СС надо иметь таблицу умножения в этой СС. Вычисление элементов такой таблицы представляет собой прибавление базовой цифры столбца к числу, стоящему на одну клетку выше. Пример таблицы умножения для двоичной СС:

Пример умножения чисел: Пример умножения чисел: 10100(2) * 1010(2) Задания: --------------- 1)1101(2)*1110(2) 101 2)4321(5)*123(5) + 101 ---------------- 11001000(2)

4) Деление. 4) Деление. При делении столбиком в P-ичной СС приходится в качестве промежуточных вычислений выполнять действия умножения и вычитания, а следовательно , используются таблицы умножения и сложения в данной P-ичной СС. Пример деления чисел: 11110(2) | 110(2) - 110(2) | 101(2) Задания: --------------- 1)10010000(2):1110(2) 110 2)4322(5):3(5) - 110 ---------------- 0

В настоящее время СС используются в основном в компьютерной технике и в информационных технологиях, однако некоторые СС применяются в других науках (математике например) или даже в повседневной жизни (например, в Китае в настоящее время используют пятеричную СС). Поэтому можно сказать , что СС востребованы и широко используются. В настоящее время СС используются в основном в компьютерной технике и в информационных технологиях, однако некоторые СС применяются в других науках (математике например) или даже в повседневной жизни (например, в Китае в настоящее время используют пятеричную СС). Поэтому можно сказать , что СС востребованы и широко используются.