Презентация на тему: Калькулятор

* Исполнители Удвоитель, Раздвоитель, Калькулятор К. Поляков, 2010 -2012 http://kpolyakov.narod.ru

* Алгоритмы Свойства алгоритма дискретность: состоит из отдельных шагов (команд) понятность: должен включать только команды, известные исполнителю (входящие в СКИ) определенность: при одинаковых исходных данных всегда выдает один и тот же результат конечность: заканчивается за конечное число шагов массовость: может применяться многократно при различных исходных данных корректность: дает верное решение при любых допустимых исходных данных Алгоритм – это четко определенный план действий для исполнителя. Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

* Удвоитель Исполнитель Удвоитель работает с одним числом и умеет выполнять с ним две операции (команды): 1. прибавь 1 2. умножь на 2 Программа – это последовательность номеров команд, которые нужно выполнить. Программа 12211 2 начальное число 3 6 12 13 14 1 2 2 1 1 результат Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

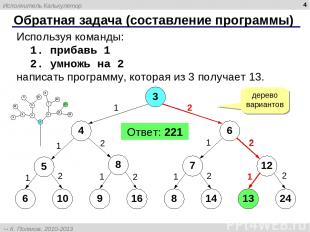
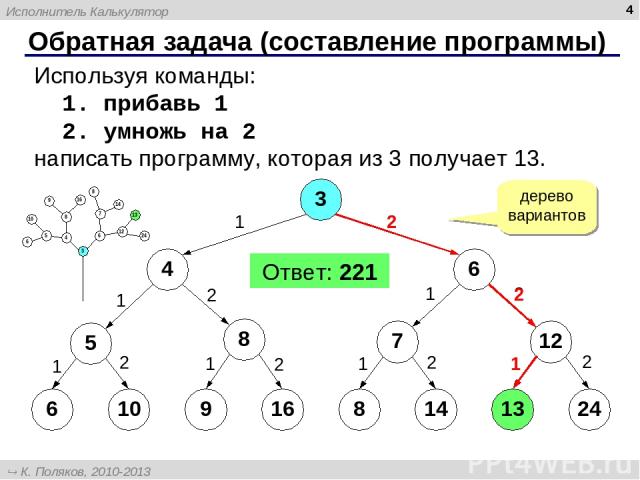
* Обратная задача (составление программы) Используя команды: 1. прибавь 1 2. умножь на 2 написать программу, которая из 3 получает 13. Ответ: 221 3 4 13 1 дерево вариантов 6 5 8 7 12 6 10 9 16 8 14 24 2 1 1 1 1 1 2 2 2 2 2 2 2 1 2 1 Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

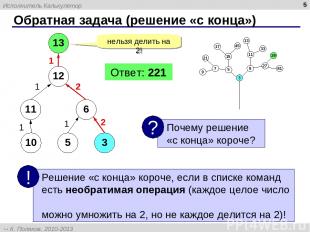
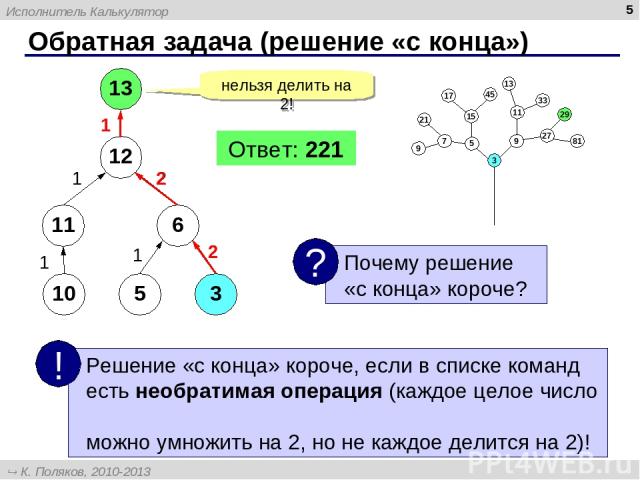
* Обратная задача (решение «с конца») 13 нельзя делить на 2! 12 11 6 10 5 3 1 1 1 2 2 2 2 1 Ответ: 221 Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

* Удвоитель У исполнителя есть команды: 1. прибавь 1 2. умножь на 2 Задания: Какие числа можно получить из 0? Как из числа 5 получить 105? Как построить самую короткую программу для получения заданного числа N из 0? Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

* Раздвоитель У исполнителя есть команды: 1. вычти 1 2. раздели на 2 Задания: Какие числа можно получить из положительного числа N? Как быстрее всего получить 0 из положительного числа N? Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

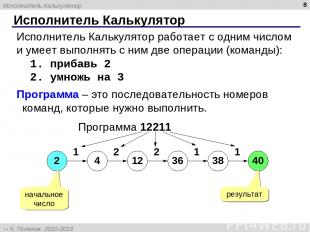
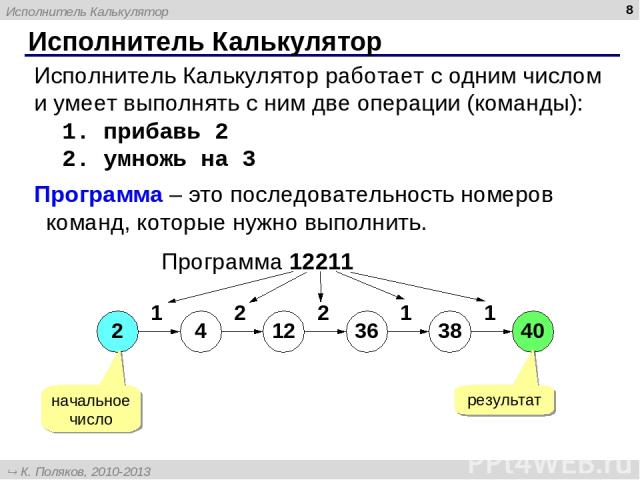
* Исполнитель Калькулятор Исполнитель Калькулятор работает с одним числом и умеет выполнять с ним две операции (команды): 1. прибавь 2 2. умножь на 3 Программа – это последовательность номеров команд, которые нужно выполнить. Программа 12211 2 начальное число 4 12 36 38 40 1 2 2 1 1 результат Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

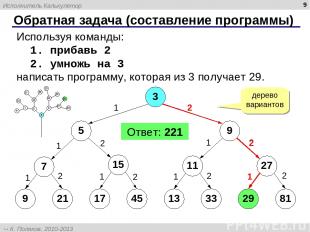
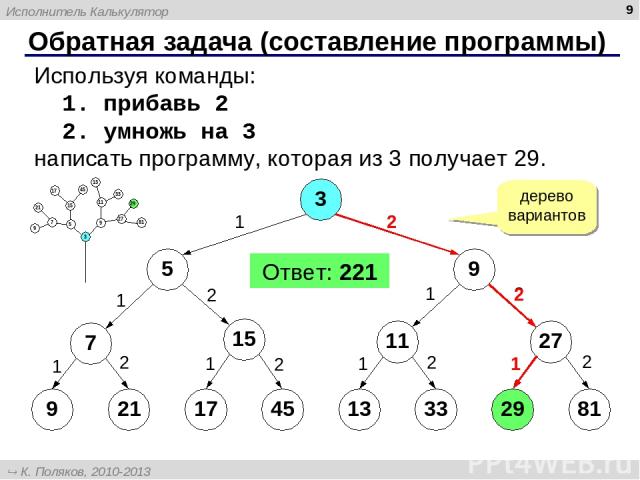
* Обратная задача (составление программы) Используя команды: 1. прибавь 2 2. умножь на 3 написать программу, которая из 3 получает 29. Ответ: 221 3 5 29 1 дерево вариантов 9 7 15 11 27 9 21 17 45 13 33 81 2 1 1 1 1 1 2 2 2 2 2 2 2 1 2 1 Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

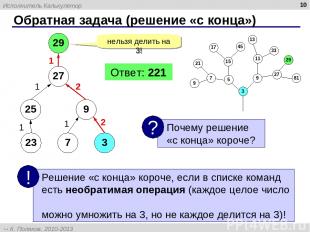
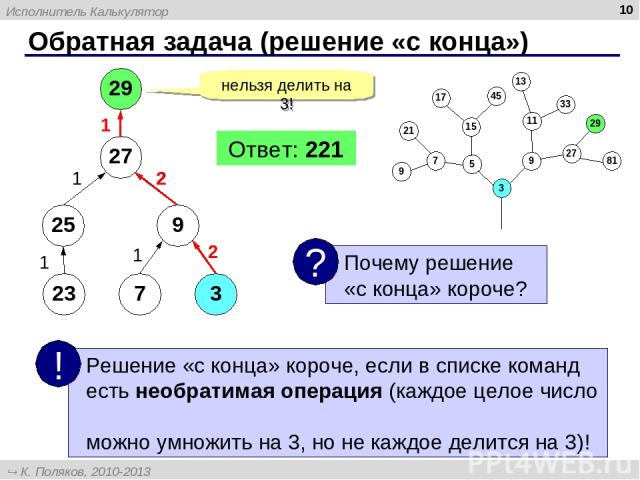
* Обратная задача (решение «с конца») 29 нельзя делить на 3! 27 25 9 23 7 3 1 1 1 2 2 2 2 1 Ответ: 221 Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

* Ещё пример Используя команды: 1. прибавь 2 2. умножь на 3 написать программу, которая из 2 получает 15. Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

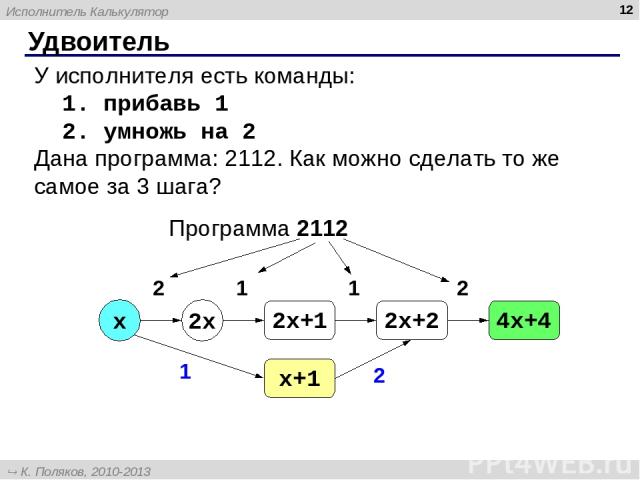
* Удвоитель У исполнителя есть команды: 1. прибавь 1 2. умножь на 2 Дана программа: 2112. Как можно сделать то же самое за 3 шага? Программа 2112 x 2x 2 1 1 2 2x+1 2x+2 4x+4 x+1 1 2 Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

* Удвоитель У исполнителя есть команды: 1. прибавь 1 2. умножь на 2 Докажите, что: любое число, меньшее 10, можно получить из 0 за 5 шагов любое число, меньшее 100, можно получить из 0 за 12 шагов Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

Длина оптимальной программы * 0 Минимальное число, для которого оптимальная программа содержит ровно N команд: первая команда – 1 (0 1) программа оканчивается на 1 (прибавь 1) при «обратном ходе» команды 1 и 2 чередуются Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

Количество программ * У исполнителя есть команды: 1. прибавь 1 2. умножь на 2 Сколько есть разных программ, с помощью которых можно из числа 1 получить число 6? Сколько есть разных программ, с помощью которых можно из числа 4 получить число 12? Сколько есть разных программ, с помощью которых можно из числа 8 получить число 18? Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

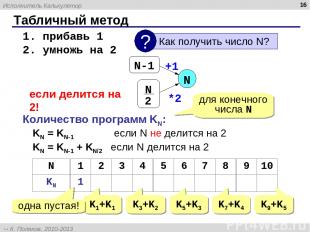
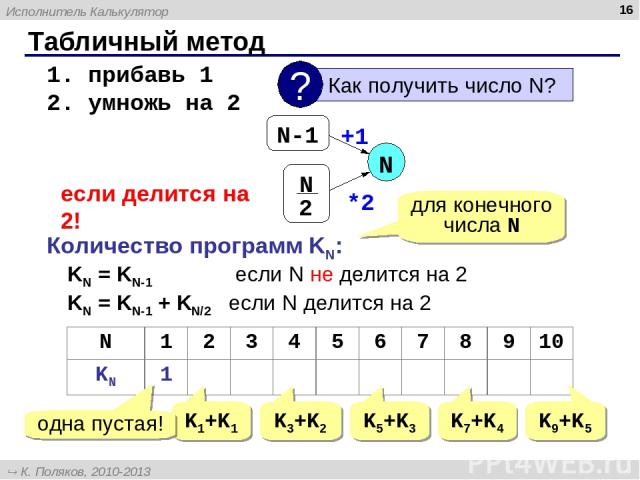
Табличный метод * 1. прибавь 1 2. умножь на 2 N если делится на 2! Количество программ KN: KN = KN-1 если N не делится на 2 KN = KN-1 + KN/2 если N делится на 2 K1+K1 K3+K2 K5+K3 K7+K4 K9+K5 +1 *2 для конечного числа N одна пустая! N 1 2 3 4 5 6 7 8 9 10 KN 1 2 2 4 4 6 6 10 10 14 Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

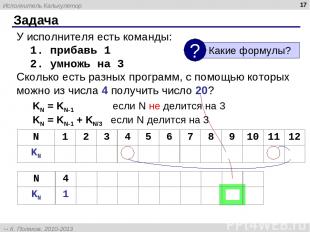
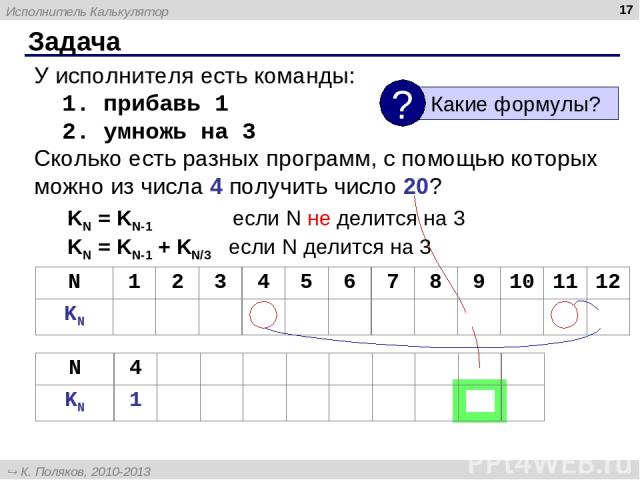
Задача * У исполнителя есть команды: 1. прибавь 1 2. умножь на 3 Сколько есть разных программ, с помощью которых можно из числа 4 получить число 20? KN = KN-1 если N не делится на 3 KN = KN-1 + KN/3 если N делится на 3 N 4 … 11 12 … 15 … 18 … 21 KN 1 1 1 2 2 3 3 4 4 5 N 1 2 3 4 5 6 7 8 9 10 11 12 KN 0 0 0 1 1 1 1 1 1 1 1 2 Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

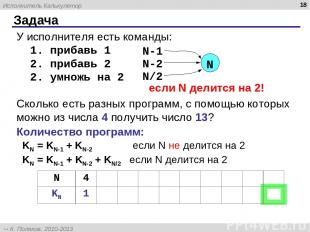
Задача * У исполнителя есть команды: 1. прибавь 1 2. прибавь 2 2. умножь на 2 Сколько есть разных программ, с помощью которых можно из числа 4 получить число 13? Количество программ: KN = KN-1 + KN-2 если N не делится на 2 KN = KN-1 + KN-2 + KN/2 если N делится на 2 N если N делится на 2! N 4 5 6 7 8 9 10 11 12 13 KN 1 1 2 3 6 9 16 25 43 68 Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

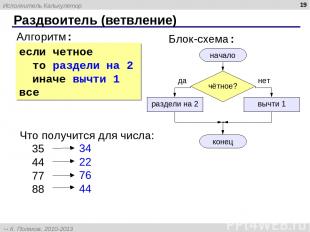
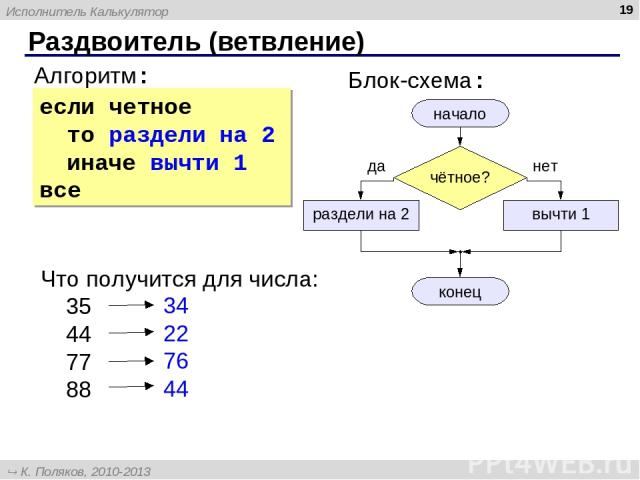
* Раздвоитель (ветвление) Алгоритм: начало конец раздели на 2 вычти 1 Блок-схема: Что получится для числа: 35 44 77 88 34 22 76 44 да нет если четное то раздели на 2 иначе вычти 1 все Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

* Раздвоитель (циклы) Алгоритм: Что получится: 10 20 30 50 60 0 1 3 3 6 Цикл – это повторение одинаковых действий. нц 5 раз если четное то раздели на 2 иначе вычти 1 всё кц если четное то раздели на 2 иначе вычти 1 всё конец цикла тело цикла начало цикла Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

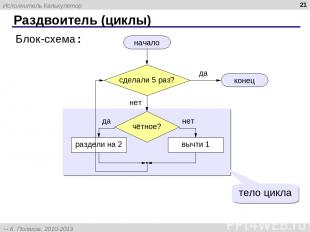
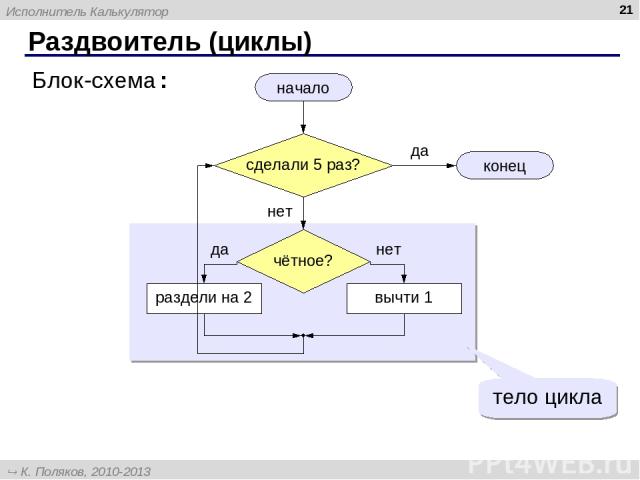
* Раздвоитель (циклы) начало конец раздели на 2 вычти 1 Блок-схема: да нет да нет тело цикла Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

нц пока положительное если четное то раздели на 2 иначе вычти 1 всё кц * Раздвоитель (циклы) Алгоритм: Задание: нарисуйте блок-схему. Сколько шагов цикла выполнится для числа 15 16 128 7 5 8 Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

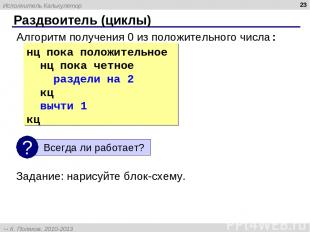
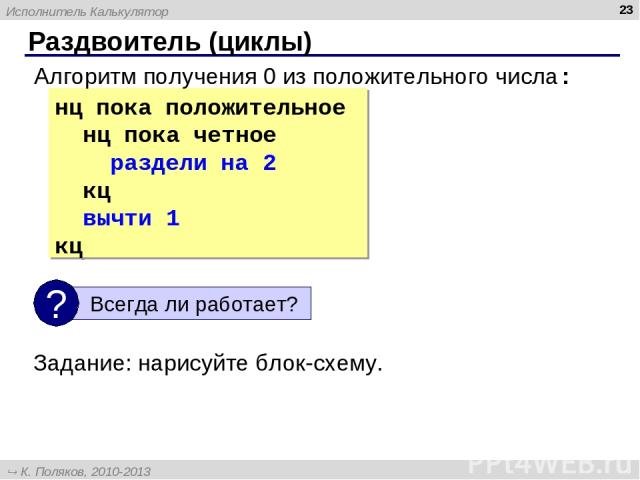
нц пока положительное нц пока четное раздели на 2 кц вычти 1 кц * Раздвоитель (циклы) Алгоритм получения 0 из положительного числа: Задание: нарисуйте блок-схему. Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

нц пока положительное вычти 1 нц пока четное раздели на 2 кц кц * Раздвоитель (циклы) Алгоритм получения 0 из положительного числа: Задание: нарисуйте блок-схему. 1? 2? 3? 4? Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

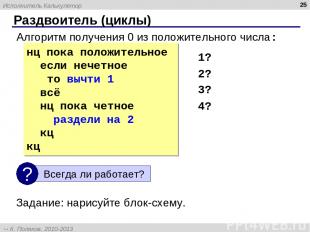
нц пока положительное если нечетное то вычти 1 всё нц пока четное раздели на 2 кц кц * Раздвоитель (циклы) Алгоритм получения 0 из положительного числа: Задание: нарисуйте блок-схему. 1? 2? 3? 4? Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

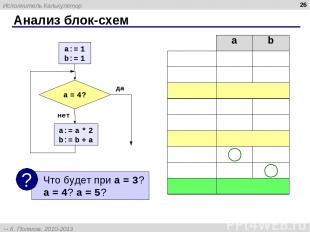
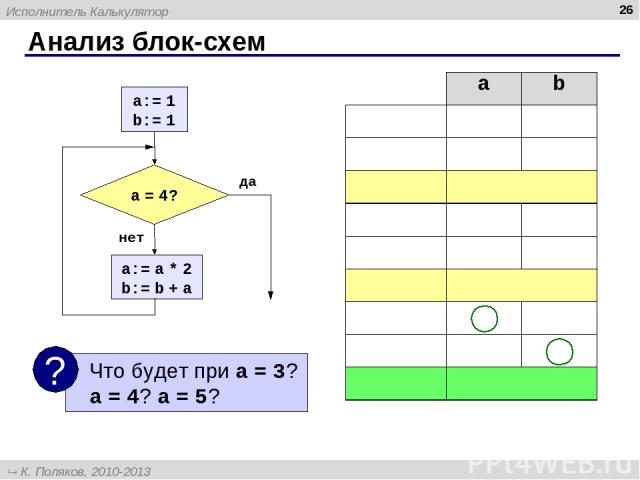
Анализ блок-схем * a b a:=1 1 ? b:=1 1 a = 4? нет a:=a*2 2 b:=b+a 3 a = 4? нет a:=a*2 4 b:=b+a 7 a = 4? да Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

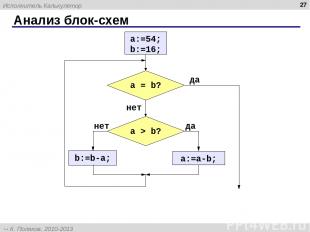
Анализ блок-схем * Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

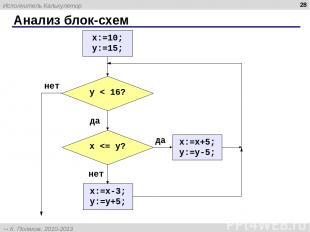
Анализ блок-схем * Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

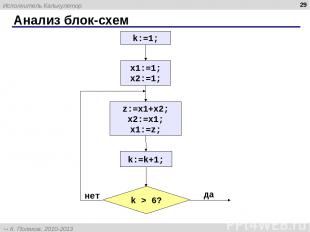
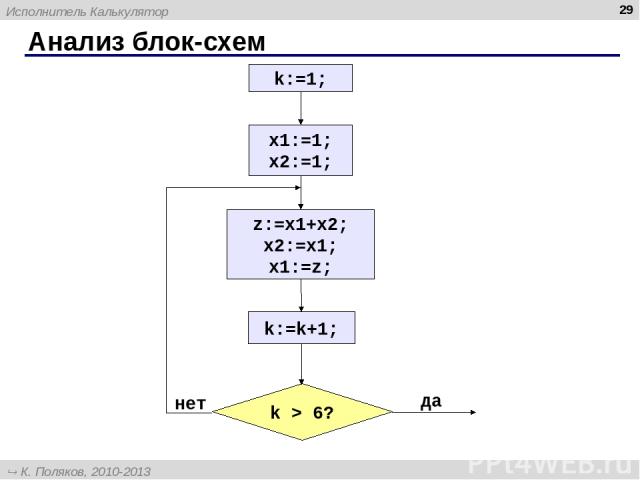
Анализ блок-схем * Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

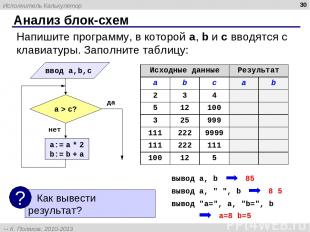
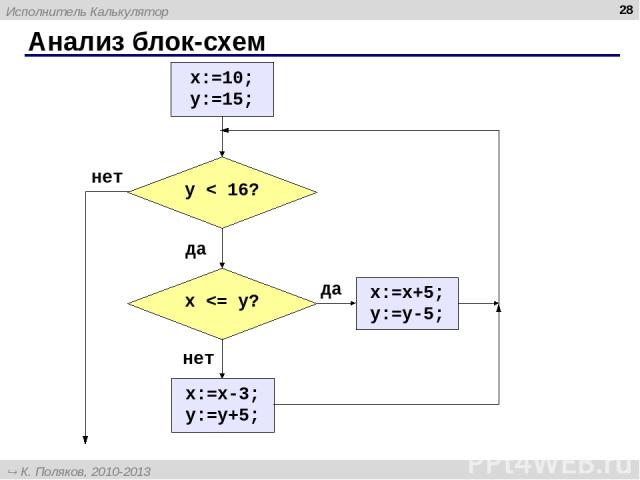
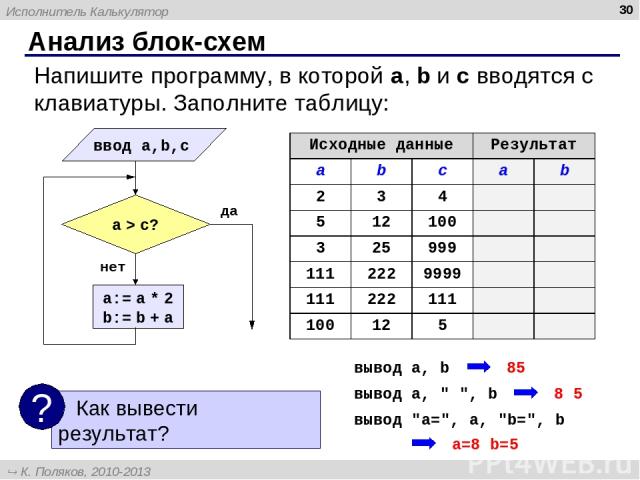
Анализ блок-схем * Напишите программу, в которой a, b и c вводятся с клавиатуры. Заполните таблицу: вывод "a=", a, "b=", b вывод a, b вывод a, " ", b Исходные данные Результат a b c a b 2 3 4 5 12 100 3 25 999 111 222 9999 111 222 111 100 12 5 Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

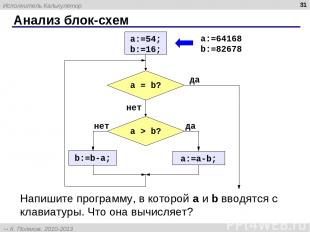
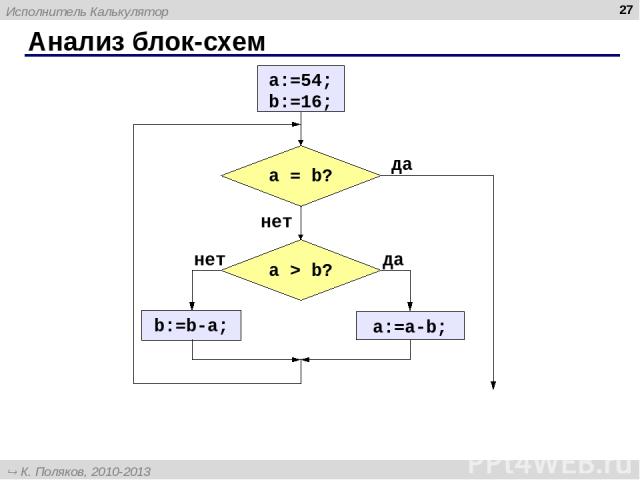
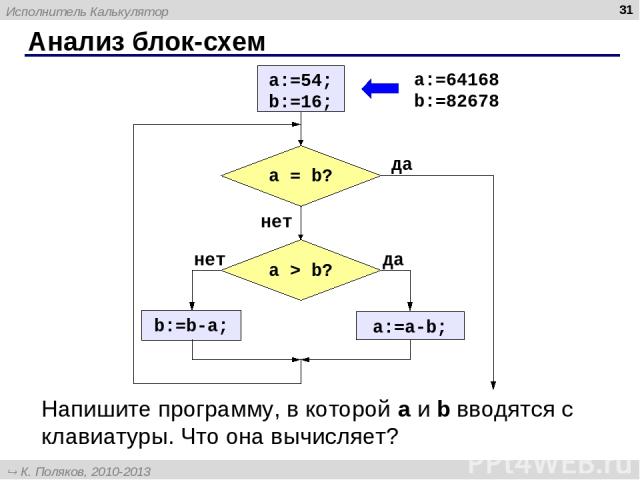
Анализ блок-схем * Напишите программу, в которой a и b вводятся с клавиатуры. Что она вычисляет? a:=64168 b:=82678 Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

Алгоритм Евклида * Евклид (365-300 до. н. э.) НОД(a,b)= НОД(a-b, b) = НОД(a, b-a) Заменяем большее из двух чисел разностью большего и меньшего до тех пор, пока они не станут равны. Это и есть НОД. НОД (14, 21) = НОД (14, 21-14) = НОД (14, 7) НОД (1998, 2) = НОД (1996, 2) = … = 2 Пример: много шагов при большой разнице чисел: = НОД (7, 7) = 7 Надо: вычислить наибольший общий делитель (НОД) чисел a и b. Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

Модифицированный алгоритм Евклида * НОД(a,b)= НОД(mod(a,b), b) = НОД(a, mod(b,a)) Заменяем большее из двух чисел остатком от деления большего на меньшее до тех пор, пока меньшее не станет равно нулю. Тогда большее — это НОД. НОД (14, 21) = НОД (14, 7) = НОД (0, 7) = 7 Пример: Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

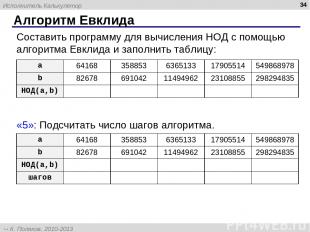
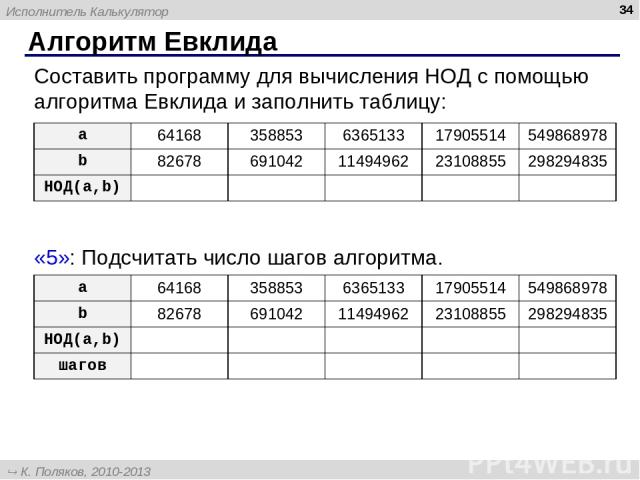
Алгоритм Евклида * Составить программу для вычисления НОД с помощью алгоритма Евклида и заполнить таблицу: «5»: Подсчитать число шагов алгоритма. a 64168 358853 6365133 17905514 549868978 b 82678 691042 11494962 23108855 298294835 НОД(a,b) a 64168 358853 6365133 17905514 549868978 b 82678 691042 11494962 23108855 298294835 НОД(a,b) шагов Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru

* Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики высшей категории, ГОУ СОШ № 163, г. Санкт-Петербург [email protected] Использованы материалы Д. Кириенко, школа № 179, г. Москва Исполнитель Калькулятор К. Поляков, 2010-2013 http://kpolyakov.spb.ru