Презентация на тему: Динамическое программирование ч.1

Динамическое программирование

Задача о нахождении минимальных затрат при строительстве транспортных артерий.

Решение задач ДП основано на принципе оптимальности. Принцип гласит: каково бы ни было начальное состояние на любом шаге последствием управления должны выбираться оптимальными исходя из конкретного состояния к которому придет система. Задачи ДП решаются или методом прямой прогонки(с 1го шага)или обратной, от конца к началу.

Пример 1 Решение методом обратной прогонки (графическое):

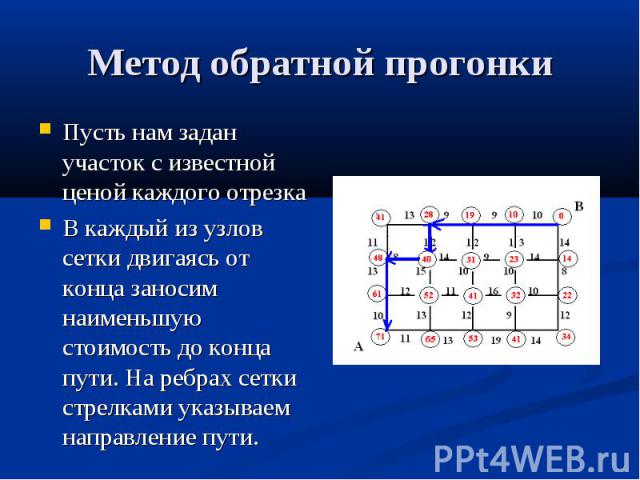
Метод обратной прогонки Пусть нам задан участок с известной ценой каждого отрезка В каждый из узлов сетки двигаясь от конца заносим наименьшую стоимость до конца пути. На ребрах сетки стрелками указываем направление пути.

Метод прямой прогонки Оптимальное распределение ресурсов

Пусть имеется некоторое количество ресурса в объеме (х) которое необходимо распределить между n различными объектами так чтобы получить суммарную эффективность, которая зависит от выбранного способа распределения.

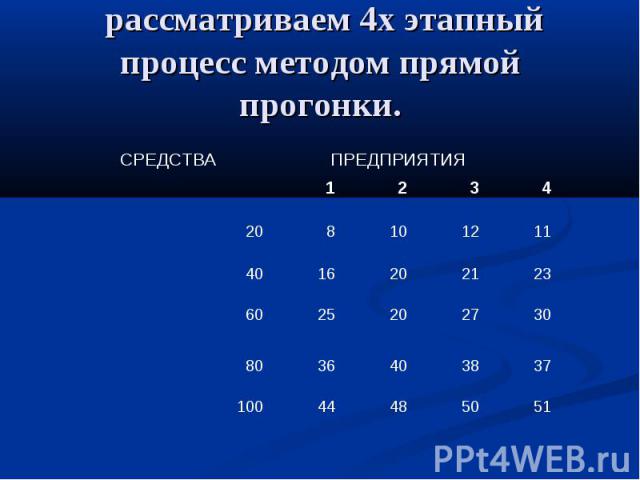
Пример 2 Совет директоров фирмы рассматривает предложение по наращиванию производственных мощностей для увеличения выпуска однородной продукции на 4х предприятиях принадлежащих фирме. Для расширения производства выделяются средства в объеме 100у.е. с дискретностью 20у.е. Прирост выпуска продукции зависит от выделенной суммы и представлены в таблице. Найти оптимальное распределение средств обеспечивающее максимальный прирост выпуска.

рассматриваем 4х этапный процесс методом прямой прогонки.

Все средства вкладываем в 1е предприятие.

Все средства вкладываем в 1е два предприятия.

Все средства вкладываем в 1е три предприятия

Все средства вкладываем в 4е предприятие.

Выписываем распределение двигаясь в обратном направлении. 4-40у.е. 3-20у.е. 2-40у.е. 1-0у.е.