Презентация на тему: Динамическое программирование в математике

Динамическое программирование в математике

Динамическое программирование это поэтапное планирование многошагового процесса, при котором на каждом этапе оптимизируется только один шаг

Планируя многоэтапную операцию, мы должны выбирать управление на каждом шаге, исходя не из узких интересов именно этого шага, Планируя многоэтапную операцию, мы должны выбирать управление на каждом шаге, исходя не из узких интересов именно этого шага, а из более широких интересов операции в целом, и далеко не всегда эти две точки зрения совпадают

Практическая часть Компания, занимающаяся производством пищевых продуктов, поставляет их для продажи в четыре города. Этим городам поставлены в соответствие торговые зоны 1, 2, 3, 4. В каждой из зон проведено изучение состояния рынка и найдены математические ожидания доходов, как функции полных капиталовложений (складские помещения, магазины, торговые уполномоченные, реклама и т.д.)

Математические ожидания доходов

Необходимо распределить имеющиеся 10 млн. рублей так, Необходимо распределить имеющиеся 10 млн. рублей так, чтобы суммарный доход по всем зонам, в которые производились вложения, был максимален.

Введем следующие обозначения: fi (x) – доход, получаемый от вложения х млн. в i-ю зону, i=1,2,3,4; F1,2(А) – максимальный доход, получаемый от вложения А млн. в зоны 1 и 2 вместе; F1,2,3(А) – максимальный доход, получаемый от вложения А млн. в зоны 1, 2 и 3 вместе; F1,2,3,4(А) – максимальный доход, получаемый от вложения А млн. в зоны 1, 2, 3 и 4 вместе.

Функцию F1,2 (А) определим равенством: F1,2(А)=max [f1 (x)+f2(A-x)]

Таким образом, чтобы определить F1,2(2), надо вычислить: f1(0)+f2(2)=0+ 0.41=0.41 f1(1)+f2(1)=0.28+0.25=0.53 f1(2)+f2(0)=0.45+0=0.45

Максимальный доход, получаемый от вложения А млн. в зоны 1 и 2 вместе

Аналогично определим функцию F1,2,3(A) формулой: F1,2,3(A)=max {F1,2(x)+f3(A-x)}

Максимальный доход, получаемый от вложения А млн. в зоны 1, 2 и 3 вместе

Теперь определим функцию F1,2,3,4(A)формулой: F1,2,3,4(A)=max {F1,2,3(x)+f4(A-x)}

Максимальный доход, получаемый от вложения А млн. в зоны 1, 2, 3 и 4 вместе

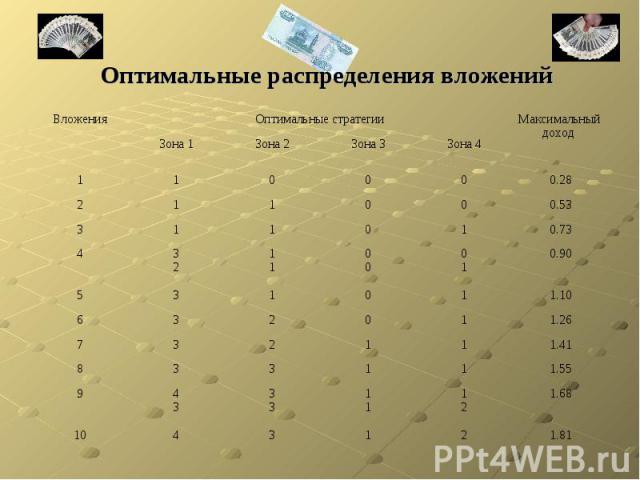
Оптимальные распределения вложений