Презентация на тему: Точка, прямая, отрезок, луч и угол


Я считаю, что без точки, прямой, отрезка, луча и угла мы не смогли бы жить. Потому что всё, на что бы не упал наш взгляд , состоит из этих составляющих. Например: книги, техника, орнаменты, деревья, картины, мебель, дома и так далее. Без их участия существуют только окружности и все, у чего нет углов. И я хочу, чтобы все обратили внимание на эти, казалось бы, незначительные вещи. Я считаю, что без точки, прямой, отрезка, луча и угла мы не смогли бы жить. Потому что всё, на что бы не упал наш взгляд , состоит из этих составляющих. Например: книги, техника, орнаменты, деревья, картины, мебель, дома и так далее. Без их участия существуют только окружности и все, у чего нет углов. И я хочу, чтобы все обратили внимание на эти, казалось бы, незначительные вещи.

1.История геометрии ( в двух частях ). 1.История геометрии ( в двух частях ). 2.Точка, прямая и отрезок: 2.1.Провешивание прямой на местности 2.2.Пересекающиеся и параллельные прямые. 3.Луч и угол. 3.1.Смежные и вертикальные углы. 3.2.Градусная мера угла

Евклид (ок. 300 до н.э.) Евклид (ок. 300 до н.э.) Греческий математик, чей главный труд «Начала» остается основой большей части современной геометрии. Одна из известных аксиом Евклидовой геометрии гласит: если дана линия и точка вне ее, то через эту точку можно провести только одну линию, параллельную первой. Эту аксиому нельзя доказать, и попытки заменить ее на другую, по которой через точку вне прямой нельзя провести ни одной линии, параллельной данной, или можно провести множество таких линий, привели к созданию в XIX веке так называемых неевклидовых геометрий ( например, геометрии Лобачевского), которые очень важны для многих сторон современной физики.

Лобачевский, Николай Иванович (1792-1856). Лобачевский, Николай Иванович (1792-1856). Русский математик, предложивший заменить один из главных постулатов геометрии Евклида о параллельных на аксиому, что в плоскости через точку, лежащую вне прямой, можно провести более одной прямой, не пересекающей первую. Это открытие, не получившее признания современников, совершило затем переворот в представлении о природе пространства и оказало огромное влияние на развитие математического мышления.
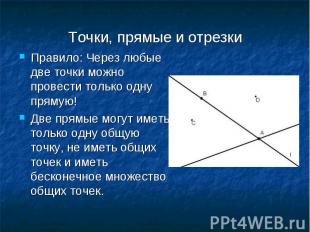
Правило: Через любые две точки можно провести только одну прямую! Правило: Через любые две точки можно провести только одну прямую! Две прямые могут иметь только одну общую точку, не иметь общих точек и иметь бесконечное множество общих точек.

Когда-то перед людьми встала такая задача: Когда-то перед людьми встала такая задача: Построить отрезок большей длины, чем сама вещь, отрезок которой строили. Как вышли из положения: просто приложили к листу бумаги линейку, отметили какие-нибудь точки A и B и лежащею между ними точку C. Затем они передвинули линейку вправо так, чтобы ее левый конец оказался около точки C, и отметили точку D около правого конца линейки. Такой прием называется провешиванием прямой на плоскости.

Существуют пересекающиеся и параллельные прямые. Существуют пересекающиеся и параллельные прямые. Пересекающимися называют линии, которые имеют хотя бы одну общую точку. Параллельными прямыми называют линии, не имеющие ни одной общей точки.
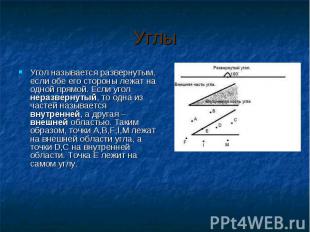
Угол называется развернутым, если обе его стороны лежат на одной прямой. Если угол неразвернутый, то одна из частей называется внутренней, а другая – внешней областью. Таким образом, точки A,B,F,I,M лежат на внешней области угла, а точки D,C на внутренней области. Точка E лежит на самом углу. Угол называется развернутым, если обе его стороны лежат на одной прямой. Если угол неразвернутый, то одна из частей называется внутренней, а другая – внешней областью. Таким образом, точки A,B,F,I,M лежат на внешней области угла, а точки D,C на внутренней области. Точка E лежит на самом углу.

Проведем прямую a и отметим на ней точку O. Эта точка разделяет прямую на две части, каждая из которых называется лучом, исходящим из точки O. Точка O называется началом каждого из лучей. Например, луч OA. Проведем прямую a и отметим на ней точку O. Эта точка разделяет прямую на две части, каждая из которых называется лучом, исходящим из точки O. Точка O называется началом каждого из лучей. Например, луч OA. Угол – это геометрическая фигура, состоящая из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – вершиной угла. Например, угол hOk.