Презентация на тему: симетрія відносно точки

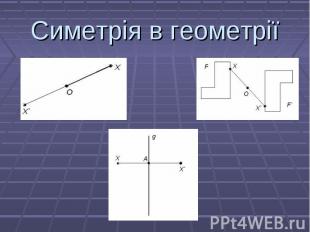
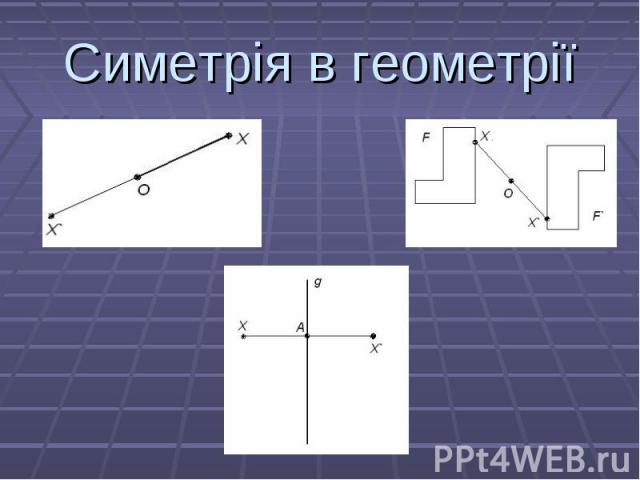
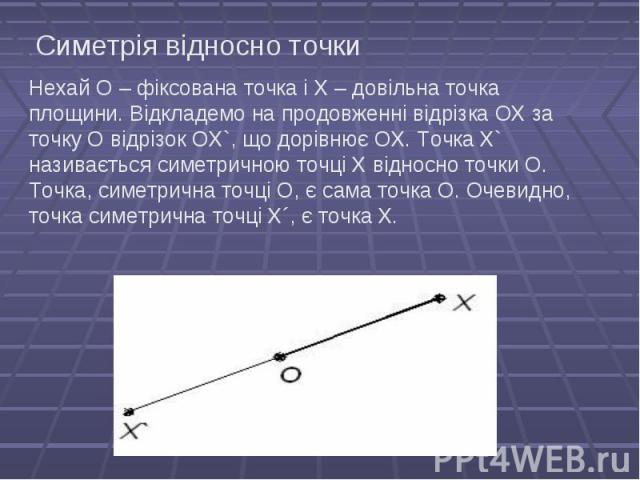
Перетворення фігури F у фігуру F`, при якому кожна її точка Х переходить у точку X`, симетричну відносно даної точки О, називається перетворенням симетрії відносно точки О. При цьому фігури F і F` називаються симетричними відносно точки О. Перетворення фігури F у фігуру F`, при якому кожна її точка Х переходить у точку X`, симетричну відносно даної точки О, називається перетворенням симетрії відносно точки О. При цьому фігури F і F` називаються симетричними відносно точки О.

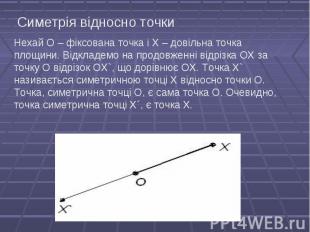
Нехай g – фіксована пряма. Візьмемо довільну точку Х і опустимо перпендикуляр АХ на пряму g. На продовженні перпендикуляра за точку А відкладемо відрізок AX`, що дорівнює відрізку АХ. Точка X` називається симетричною точці Х відносно прямої g. Якщо точка Х лежить на прямій g, то симетрична їй точка є сама точка Х. Очевидно, що точка, симетрична точці X`, є точка Х. Нехай g – фіксована пряма. Візьмемо довільну точку Х і опустимо перпендикуляр АХ на пряму g. На продовженні перпендикуляра за точку А відкладемо відрізок AX`, що дорівнює відрізку АХ. Точка X` називається симетричною точці Х відносно прямої g. Якщо точка Х лежить на прямій g, то симетрична їй точка є сама точка Х. Очевидно, що точка, симетрична точці X`, є точка Х.

Перетворення фігури F у фігуру F`, при якому кожна її точка Х переходить у точку X`, симетричну відносно даної прямої g, називається перетворенням симетрії відносно прямої g. При цьому фігури F і F` називаються симетричними відносно прямої g. Перетворення фігури F у фігуру F`, при якому кожна її точка Х переходить у точку X`, симетричну відносно даної прямої g, називається перетворенням симетрії відносно прямої g. При цьому фігури F і F` називаються симетричними відносно прямої g.

Більшість простих молекул володіють елементами просторової симетрії рівноважної конфігурації: осями симетрії, плоскістю симетрії Так, молекула аміаку Nh 3 володіє симетрією правильної трикутної піраміди Більшість простих молекул володіють елементами просторової симетрії рівноважної конфігурації: осями симетрії, плоскістю симетрії Так, молекула аміаку Nh 3 володіє симетрією правильної трикутної піраміди молекула метану Ch 4 — симетрією тетраедра.

Поняття симетрії відіграє велику роль у фізиці. Перш за все слід відзначити просторову симетрію, якою можуть характеризуватися фізичні об'єкти. Тут слід розрізняти симетрію щодо трансляції, симетрію щодо дзеркального відображення, симетрію щодо поворотів, гвинтову симетрію тощо. Особливим видом симетрії є ізотропність - незалежність властивостей фізичної системи від напрямку, однорідність - незалежність властивостей фізичної системи від точки простору. Специфічним для фізики видом симетрії є інваріантність фізичних законів щодо вибору системи відліку, яка лежить в основі теорії відносності. Іншим видом симетрії, який зустрічається в фізиці є симетрія щодо заміни напрямку координатних осей, що лежить в основі принципу парності.

Ромб має 2 віс симетрії– це його діагоналі Ромб має 2 віс симетрії– це його діагоналі

У рівнобедреному трикутрику є 1 вісь– це медіана,бісектриса і висота проведена до основи У рівнобедреному трикутрику є 1 вісь– це медіана,бісектриса і висота проведена до основи

У рівностороньому трикутнику є 3 вісі симетрії: бісектриси, медіани і висоти трикутника У рівностороньому трикутнику є 3 вісі симетрії: бісектриси, медіани і висоти трикутника

У квадрата є 4 вісі симетрії У квадрата є 4 вісі симетрії

А круг це єдина фігура у якої є безліч осей симетрії, що містять діаметри кола. Круг симетричний сам собі. А круг це єдина фігура у якої є безліч осей симетрії, що містять діаметри кола. Круг симетричний сам собі.

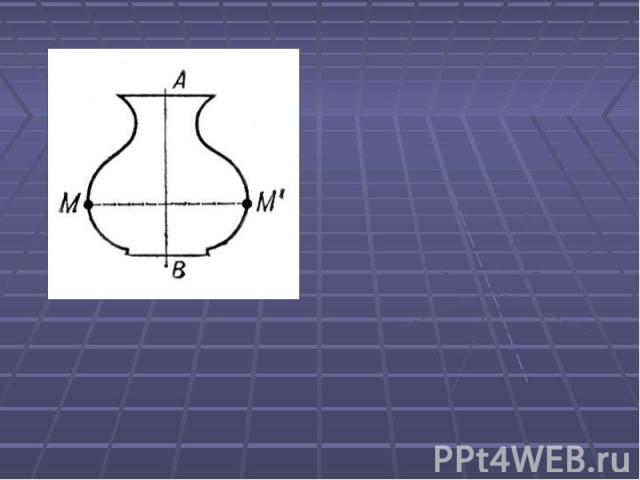
Щоб побачити симетрію не потрібно розгортити книжки з геометрії, достатньо просто подивитися навколо... Багато побутових предметів є симетричеими. Щоб побачити симетрію не потрібно розгортити книжки з геометрії, достатньо просто подивитися навколо... Багато побутових предметів є симетричеими. Наприклад: глечик,зірка...

Навіть в орнаменті можна повести чимало осей симетрії Навіть в орнаменті можна повести чимало осей симетрії

Також у природі нас також оточує симетрія Також у природі нас також оточує симетрія

Але найлегший спосіб побачити симетрію це просто подивитись на оточуючих людей, або ж глянути у дзеркало. Але найлегший спосіб побачити симетрію це просто подивитись на оточуючих людей, або ж глянути у дзеркало.

Це питання здається смішним. Звісно що симетричні! Але тут можна дискутувати. Адже у природі немає нічого ідеально рівного. Ніхто не може дати гарантії, що його очі знаходяться на однаковій відстані від умовної лінії симетрії. Це питання здається смішним. Звісно що симетричні! Але тут можна дискутувати. Адже у природі немає нічого ідеально рівного. Ніхто не може дати гарантії, що його очі знаходяться на однаковій відстані від умовної лінії симетрії.