Презентация на тему: Основные аксиомы стереометрии

Первые уроки стереометрии 10 класс МСОШ№1 Шахвалеева С.В. 5klass.net

Скажи мне – и я забуду. Покажи мне – и я запомню. Вовлеки меня – и я научусь. Древняя китайская пословица

Четыре равносторонних треугольника

Геометрия Планиметрия Стереометрия stereos пространственный

Предмет стереометрии. СТЕРЕОМЕТРИЯ – это раздел геометрии, в котором изучаются свойства фигур в пространстве. Первый дошедший до нас учебник – руководство по математике под названием «Начала», созданное древнегреческим ученым Евклидом в III в. до н. э.

Пирамида Хеопса
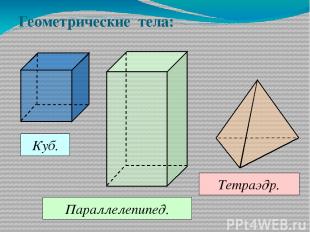
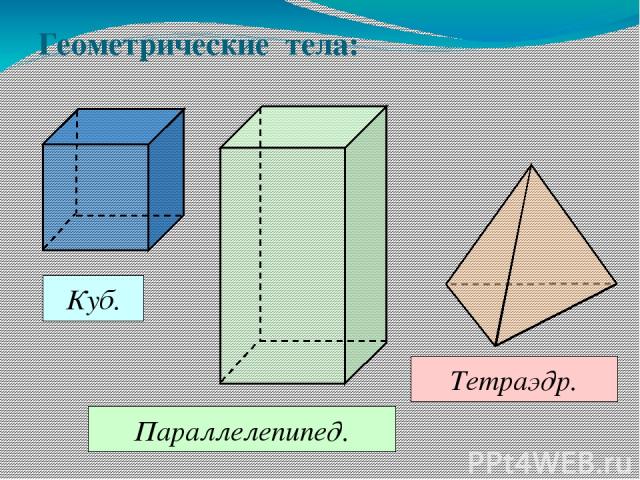
Геометрические тела: Куб. Параллелепипед. Тетраэдр.
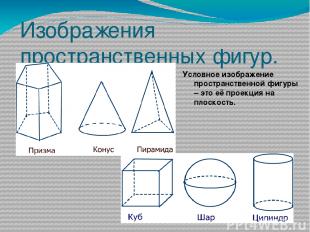
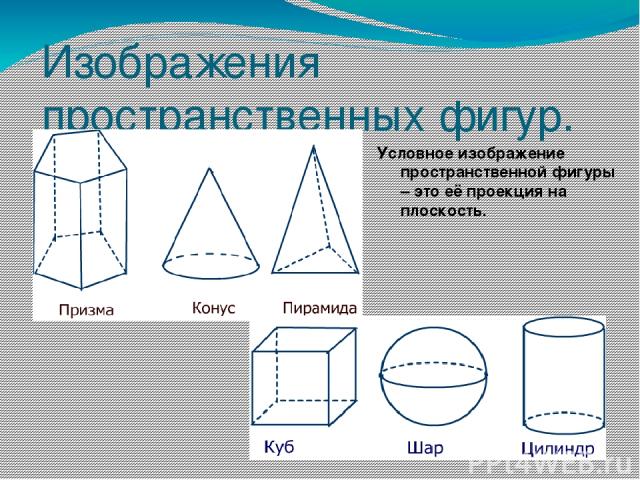
Изображения пространственных фигур. Условное изображение пространственной фигуры – это её проекция на плоскость.
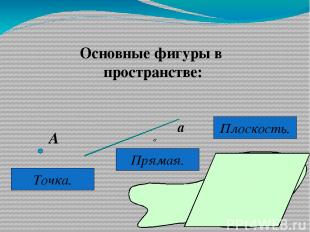
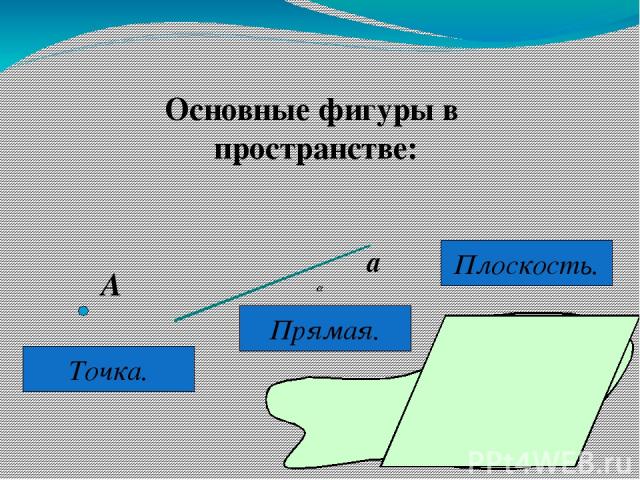
Основные фигуры в пространстве: А Точка. а Прямая. Плоскость.

A, B, C, … a, b, c, … или AВ, BС, CD, …

Аксиома (от греч. axíõma – принятие положения) исходное положение научной теории, принимаемое без доказательства

А1: Через любые три точки, не лежащие на одной прямой проходит плоскость, и притом только одна. ВОПРОСЫ: -всегда ли три точки лежат в одной плоскости? -всегда ли четыре точки лежат в одной плоскости? -всегда ли через три точки проходит плоскость, и притом только одна? -сколько плоскостей можно провести через две точки?

А2: Если две точки прямой лежат в плоскости, то все точки этой прямой лежат в плоскости. ВОПРОСЫ: верно ли утверждение: -если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости? - а если три точки окружности лежат в плоскости, то …?

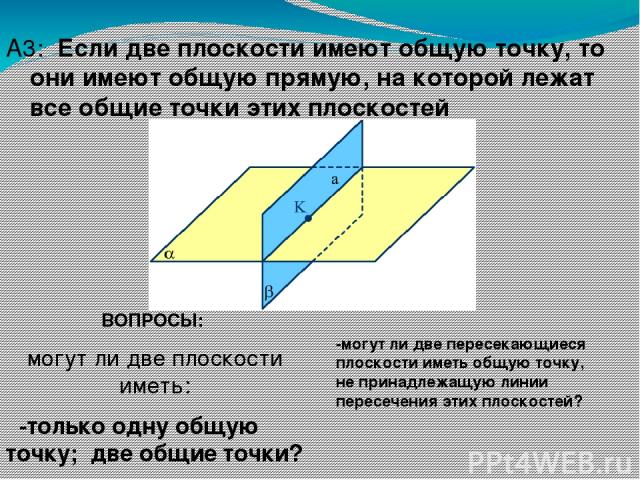
А3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей ВОПРОСЫ: могут ли две плоскости иметь: -только одну общую точку; две общие точки? -только одну общую прямую? -могут ли две пересекающиеся плоскости иметь общую точку, не принадлежащую линии пересечения этих плоскостей?

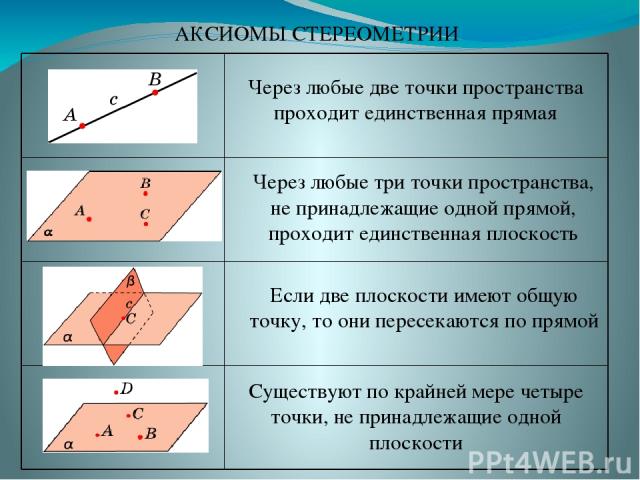
АКСИОМЫ СТЕРЕОМЕТРИИ Через любые две точки пространства проходит единственная прямая Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная плоскость Если две плоскости имеют общую точку, то они пересекаются по прямой Существуют по крайней мере четыре точки, не принадлежащие одной плоскости

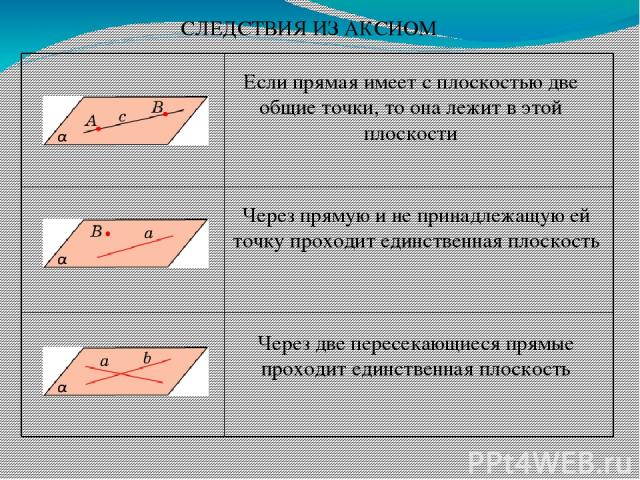
СЛЕДСТВИЯ ИЗ АКСИОМ Если прямая имеет с плоскостью две общие точки, то она лежит в этой плоскости Через прямую и не принадлежащую ей точку проходит единственная плоскость Через две пересекающиеся прямые проходит единственная плоскость
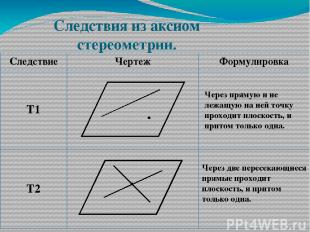
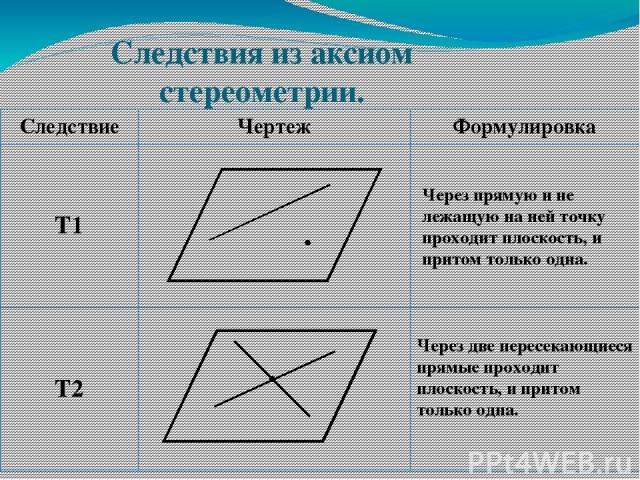
Следствия из аксиом стереометрии. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Через две пересекающиеся прямые проходит плоскость, и притом только одна. Следствие Чертеж Формулировка Т1 Т2

Источники и ссылки: Атанасян Л.С. Учебник «Геометрия 10-11», -М.: Просвещение, 2009г. Болтянский В.Г. Элементарная геометрия. Книга для учителя. – М.: Просвещение, 1999г. https://www.google.ru/search?