Презентация на тему: Как найти длину окружности

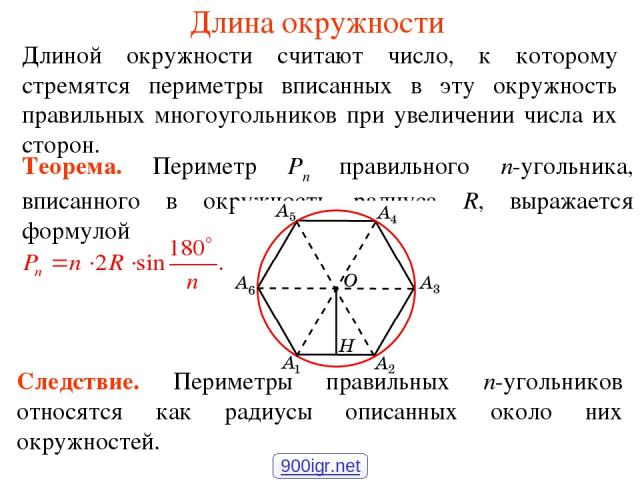
Длина окружности Длиной окружности считают число, к которому стремятся периметры вписанных в эту окружность правильных многоугольников при увеличении числа их сторон. Следствие. Периметры правильных n-угольников относятся как радиусы описанных около них окружностей. 900igr.net

Длина окружности Половина длины окружности единичного радиуса обозначается греческой буквой π. Таким образом, длина окружности единичного радиуса равна 2π. Из рассмотренной выше теоремы следует, что длина окружности радиуса R равна 2πR. Таким образом, для длины окружности C радиуса R можем записать следующую формулу: C = 2πR. Теорема. Отношение длин двух окружностей равно отношению их радиусов.

Приближенное вычисление числа π

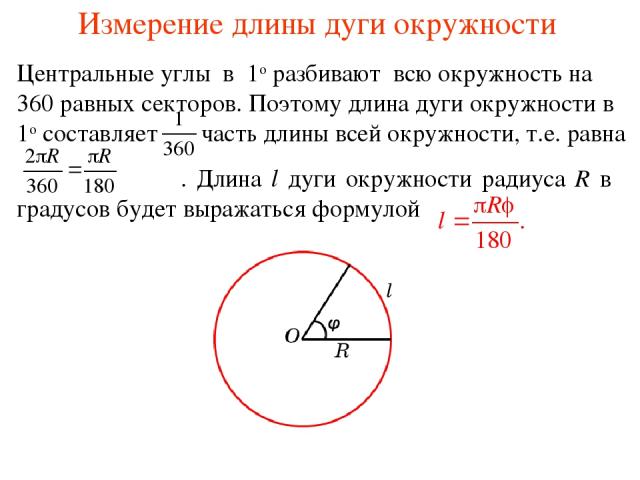
Измерение длины дуги окружности Центральные углы в 1о разбивают всю окружность на 360 равных секторов. Поэтому длина дуги окружности в 1о составляет часть длины всей окружности, т.е. равна . Длина l дуги окружности радиуса R в φ градусов будет выражаться формулой

Измерение угла окружности Равенство , выражающее длину дуги единичной окружности, устанавливает соответствие между длиной дуги и ее градусной мерой. Это позволяет измерять углы не только с помощью градусов, но и с помощью длины дуги соответствующей окружности единичного радиуса. Величина длины дуги называется радианной мерой угла. Единицей радианной меры углов является радиан. Угол в один радиан – это угол, для которого длина соответствующей дуги единичной окружности равна единице.

Вопрос 1 Что считается длиной окружности? Ответ. Длиной окружности считают число, к которому стремятся периметры вписанных в эту окружность правильных многоугольников при увеличении числа их сторон.

Вопрос 2 Как выражается периметр правильного n-угольника через радиус описанной окружности?

Вопрос 3 Как относятся периметры двух правильных n-угольников? Ответ. Периметры правильных n-угольников относятся как радиусы описанных около них окружностей.

Вопрос 4 Как относятся длины двух окружностей? Ответ. Отношение длин двух окружностей равно отношению их радиусов.

Вопрос 5 Что обозначает греческая буква π? Ответ. Греческая буквой π обозначает половину длины окружности единичного радиуса.

Вопрос 6 Чему равна длина окружности радиуса R? Ответ. Длина окружности радиуса R равна 2πR.

Вопрос 7 Какие неравенства выполняются для числа π?

Вопрос 8 Каково приближенное значение числа π? Ответ. Приближенное значение числа π берется равным 3,14.

Вопрос 9 Чему равна длина дуги окружности в 1о?

Вопрос 10 Чему равна длина дуги окружности в φ градусов?

Вопрос 11 Чему равна градусная мера угла в один радиан?

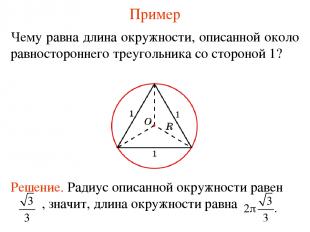
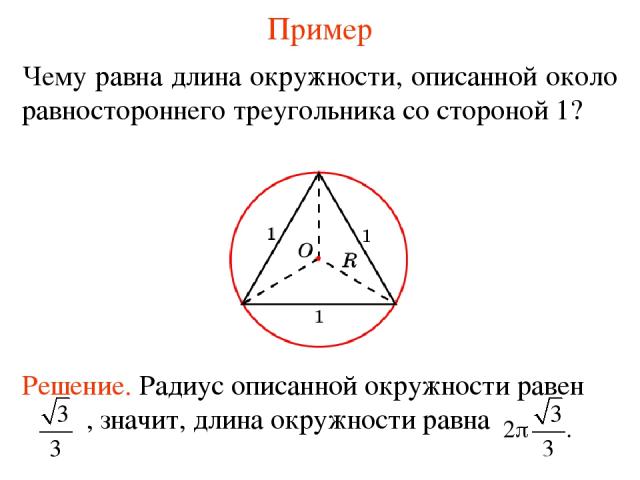
Пример Чему равна длина окружности, описанной около равностороннего треугольника со стороной 1?

Упражнение 1 Как изменится длина окружности, если радиус окружности: а) увеличить в три раза; б) уменьшить в два раза? Ответ: а) Увеличится в три раза; б) уменьшится в два раза.

Упражнение 2 Найдите длину окружности, описанной около квадрата со стороной а?

Упражнение 3 Найдите длину дуги окружности радиуса единица, соответствующей центральному углу в: а) 30о; б) 135о; в) 240о; г) 315о.

Упражнение 4 Каким должен быть радиус окружности, в которой дуга в 1о имеет длину 1 см? Укажите приближенное значение, равное целому числу сантиметров.

Упражнение 5 Какой длины должна быть хорда в окружности радиуса R, чтобы длины дуг, на которые она разбивает окружность, относились как 2:1?

Упражнение 6 Найдите периметр правильного n-угольника, описанного около окружности радиуса R.

Упражнение 7 Рассмотрев правильные шестиугольники, вписанный и описанный около окружности единичного радиуса, найдите нижнюю и верхнюю оценки для числа π.

Упражнение 8 Внутри окружности радиуса R расположены три равные окружности, которые касаются друг друга и данной окружности. Найдите их радиус.

Упражнение 9 Найдите радианную меру углов в: а) 30о; б) 45о; в) 60о.

Упражнение 10 Ответ: а) 90о; Найдите градусную меру угла, если его радианная мера равна: а) ; б) ; в) ; г) ; д) ; е) . б) 45о; в) 22о30'; г) 150о; д) 70о; е) 240о.

Упражнение 11 Найдите радиус земного шара, исходя из того, что 1 м составляет одну сорокамиллионную долю длины экватора.

Упражнение 12 Вообразите, что земной шар плотно обтянут по экватору веревкой. На сколько нужно увеличить длину веревки, чтобы ее можно было поднять над поверхностью Земли по всей длине на расстояние 1 м? Ответ: На 2π м.