Презентация на тему: УМК по физике

УМК «Физика. 7-9 класс» автор: Степанова Г.Н. д.п.н., профессор кафедры физико-математического образования Санкт-Петербургской Академии постдипломного педагогического образования Рекомендовано Министерством образования и науки РФ 900igr.net

Особенности учебника Информация представлена в двух параллельных рядах: вербальном и графическом В основе курса экспериментальный подход к изучению и исследованию явлений В основе курса лежит деятельностный подход к обучению

Структура содержания

9 класс электростатика магнитное поле колебания различной природы волны различной природы оптика

ВВЕДЕНИЕ 1.ЯВЛЕНИЯ ОКРУЖАЮЩЕГО МИРА 2.МЫ — НАБЛЮДАТЕЛИ (КАК ЕСТЕСТВОИСПЫТАТЕЛИ ПОЗНАЮТ МИР) 3.ДЛЯ ЧЕГО ЧЕЛОВЕКУ НУЖНЫ НАУЧНЫЕ ЗНАНИЯ О ПРИРОДЕ? 4. ТЕЛА И ВЕЩЕСТВА 5. ПОДВОДЯТ ЛИ НАС ОРГАНЫ ЧУВСТВ? 6. ИЗМЕРЕНИЯ И ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ ПРАКТИКУМ № 1. УЧИМСЯ РЕШАТЬ ЗАДАЧИ ПОДВЕДЁМ ИТОГИ Содержание

ОСНОВЫ КИНЕМАТИКИ 7. МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ И ЕГО ОПИСАНИЕ 8. СИСТЕМА ОТСЧЁТА. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТЕЛА В ПРОСТРАНСТВЕ. МАТЕРИАЛЬНАЯ ТОЧКА Практическая работа № 1. Определение положения тела в лабораторной системе отсчёта 9. ОСНОВНЫЕ ПОНЯТИЯ КИНЕМАТИКИ 10. РАВНОМЕРНОЕ И НЕРАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ Практическая работа № 2. Изучение прямолинейного движения тел 11. СКОРОСТЬ ТЕЛА ПРИ РАВНОМЕРНОМ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ 12. РАВНОМЕРНОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ. СПОСОБЫ ОПИСАНИЯ ДВИЖЕНИЯ 13. СКОРОСТЬ НЕРАВНОМЕРНОГО ДВИЖЕНИЯ. СРЕДНЯЯ СКОРОСТЬ Практическая работа № 3. Измерение средней скорости неравномерного движения 14. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ 15. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ 16. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ 17. ОТНОСИТЕЛЬНОСТЬ МЕХАНИЧЕСКОГО ДВИЖЕНИЯ ПРАКТИКУМ № 2. УЧИМСЯ РЕШАТЬ ЗАДАЧИ ПОДВЕДЁМ ИТОГИ

ОСНОВЫ ДИНАМИКИ 18. ВЗАИМОДЕЙСТВИЕ ТЕЛ. ПЕРВЫЙ ЗАКОН НЬЮТОНА 19. ИНЕРЦИЯ 20. МАССА ТЕЛА И ЕЁ ИЗМЕРЕНИЕ Практическая работа № 4. Измерение массы тела 21. ПЛОТНОСТЬ ВЕЩЕСТВА Практическая работа № 5. Определение плотности вещества 22. СИЛА. ВТОРОЙ ЗАКОН НЬЮТОНА 23. СЛОЖЕНИЕ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СИЛА 24. ТРЕТИЙ ЗАКОН НЬЮТОНА ПРАКТИКУМ № 3. УЧИМСЯ РЕШАТЬ ЗАДАЧИ ПОДВЕДЁМ ИТОГИ

СИЛЫ В ПРИРОДЕ 25. СИЛА УПРУГОСТИ. ЗАКОН ГУКА Практическая работа № 6. Изучение зависимости модуля деформации пружины или резины от величины нагрузки 26. ВСЕМИРНОЕ ТЯГОТЕНИЕ. СИЛА ТЯЖЕСТИ Практическая работа № 7. Изучение зависимости силы тяжести от массы тела 27. ДВИЖЕНИЕ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ 28. ВЕС ТЕЛА. НЕВЕСОМОСТЬ 29. СИЛА ДАВЛЕНИЯ. ДАВЛЕНИЕ. ПЕРЕДАЧА ДАВЛЕНИЯ ТВЁРДЫМИ ТЕЛАМИ 30. СИЛА ТРЕНИЯ Практическая работа № 8. Изучение силы трения скольжения 31. СИЛА ТРЕНИЯ ПОКОЯ ПРАКТИКУМ № 4. УЧИМСЯ РЕШАТЬ ЗАДАЧИ ПОДВЕДЁМ ИТОГИ

ЗАКОНЫ СОХРАНЕНИЯ 32. ИМПУЛЬС ТЕЛА И ИМПУЛЬС СИЛЫ 33. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА 34. РЕАКТИВНОЕ ДВИЖЕНИЕ 35. МЕХАНИЧЕСКАЯ РАБОТА 36. МОЩНОСТЬ 37. РАБОТА СИЛЫ ТЯЖЕСТИ 38. РАБОТА СИЛЫ ТРЕНИЯ 39. ЭНЕРГИЯ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ 40. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ 41. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ.ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ ПРАКТИКУМ № 5. УЧИМСЯ РЕШАТЬ ЗАДАЧИ ПОДВЕДЁМ ИТОГИ

РАВНОВЕСИЕ ТЕЛ. ПРОСТЫЕ МЕХАНИЗМЫ 42. РАВНОВЕСИЕ ТВЁРДЫХ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ Практическая работа № 9. Определение положения центра масс тела 43. РАВНОВЕСИЕ ТЕЛА, ЗАКРЕПЛЁННОГО НА ОСИ.ПРАВИЛО РЫЧАГА Практическая работа № 10. Выяснение условий равновесия рычага 44. ИСПОЛЬЗОВАНИЕ РЫЧАГА 45. НЕПОДВИЖНЫЙ И ПОДВИЖНЫЙ БЛОКИ 46. НАКЛОННАЯ ПЛОСКОСТЬ Практическая работа № 11. Изучение наклонной плоскости § 47. «ЗОЛОТОЕ ПРАВИЛО» МЕХАНИКИ ПРАКТИКУМ № 6. УЧИМСЯ РЕШАТЬ ЗАДАЧИ ПОДВЕДЁМ ИТОГИ

48. ОСНОВНЫЕ СВОЙСТВА ЖИДКОСТЕЙ И ГАЗОВ 49. ПЕРЕДАЧА ДАВЛЕНИЯ ЖИДКОСТЯМИ И ГАЗАМИ 50. ДАВЛЕНИЕ ЖИДКОСТИ НА ДНО И СТЕНКИ СОСУДА Практическая работа № 12. Обнаружение давления жидкости на дно и стенки сосуда 51. СООБЩАЮЩИЕСЯ СОСУДЫ 52. ГИДРАВЛИЧЕСКИЕ МАШИНЫ 53. АТМОСФЕРНОЕ ДАВЛЕНИЕ 54. БАРОМЕТР-АНЕРОИД 55. ДЕЙСТВИЕ ЖИДКОСТИ НА ПОГРУЖЕННОЕ В НЕЁ ТЕЛО Практическая работа № 13. Изучение действия жидкости на погруженное в неё тело 56. АРХИМЕДОВА СИЛА 57. ПЛАВАНИЕ ТЕЛ 58. ВОЗДУХОПЛАВАНИЕ ПРАКТИКУМ № 7. УЧИМСЯ РЕШАТЬ ЗАДАЧИ ПОДВЕДЕМ ИТОГИ ПРЕДМЕТНО–ИМЕННОЙ УКАЗАТЕЛЬ ОСНОВЫ ГИДРО-И АЭРОСТАТИКИ

9 класс электростатика магнитное поле колебания различной природы волны различной природы оптика

Пример практической работы Практическая работа № 1 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ТЕЛА В ЛАБОРАТОРНОЙ СИСТЕМЕ ОТСЧЁТА Подберите несколько тел разных размеров. Необходимо научиться определять положение этих тел на поверхности стола в выбранной системе отсчёта. Расположите эти тела на столе произвольным образом. Выберите одно из них — пусть оно будет телом отсчёта. Возьмите две длинные узкие полоски бумаги и нанесите на них штрихи, так чтобы расстояние между ними было равно 1 или 2 см. Используйте эти полоски бумаги в качестве осей системы координат. Укажите на них начало отсчёта. Задание 1. Определите положение каждого из тел в этой системе отсчёта и запишите их координаты. Форму записи предложите самостоятельно. Задание 2. Не меняя положения тел на столе, перенесите координатные оси так, чтобы начало отсчёта совпало с положением другого тела (новое тело отсчёта). Определите положение каждого тела в новой системе отсчёта и запишите их координаты. Сравните между собой координаты каждого тела в разных системах отсчёта. Какой вывод можно сделать? Запишите его. Задание 3. Оставьте на столе только два тела: одно будет телом отсчёта. Выберите наиболее удобное расположение координатных осей. Запишите начальные координаты другого тела в этой системе отсчёта. Измените положение этого тела на столе и снова определите и запишите его координаты. Какой вывод можно сделать? Запишите его.

ПРАКТИКУМ № 2. УЧИМСЯ РЕШАТЬ ЗАДАЧИ Задачи по теме «Основы кинематики» разобьём на три группы: качественные задачи, графические и расчётные. Это позволит нам более отчётливо выделить три основных умения, которые требуются человеку при решении любой задачи. Первое — это умение провести рассуждение, приводящее к ответу на поставленный вопрос, не прибегая к формулам. Второе — умение извлекать информацию из графика и на её основе получать новое знание. Для этого научимся задавать вопросы, развивая ситуацию, описанную в задаче. Третье — это умение получать новое знание в процессе применения формул. (Конечно, это деление условное, ведь прежде, чем начать применять формулу, нужно провести рассуждение, которое позволит выбрать «нужную формулу». А при решении графических и качественных задач часто полезно провести некоторые вычисления.) Мы приведём примеры решения типовых задач, но при этом не будем придерживаться последовательности изложения материала в учебнике. Вы сами отберёте задачи по тому материалу, который к данному моменту времени уже изучен, а ещё лучше, если будете учиться их решать, когда весь теоретический материал темы изучен. Желаю успеха! Качественные задачи Задача 1. В каких из перечисленных случаев тело можно принять за материальную точку: а) определяют положение самолёта, выполняющего рейс из Санкт-Петербурга в Москву; б) определяют объём тела при помощи мензурки; в) определяют скорость движения Марса вокруг Солнца; г) измеряют массу тела при помощи весов.

Рассуждения Форма записи Каждое из перечисленных тел — это реальные тела, имеющие вполне определенную форму и размеры. Материальная точка — это физическая модель тела. Заменить тело моделью можно только при определённых условиях. Эти условия нужно перечислить. Условия, при которых тело можно принять за материальную точку:1. Тело движется поступательно. 2. Размеры тела малы по сравнению с расстоянием до наблюдателя. 3. Размеры тела малы по сравнению с расстоянием, которое оно проходит при рассматриваемом движении. Теперь каждую ситуацию в отдельности надо сопоставить с перечисленными условиями. В случае необходимости полезно найти дополнительную информацию в справочной литературе. В случае а самолёт можно принять за материальную точку, так как одновременно выполняются все три условия. Дополнительные сведения. Длина пассажирского реактивного самолёта составляет примерно 50 м, а расстояние от Санкт- Петербурга до Москвы — около 650 км, то есть более чем в 10 000 раз больше. Случай а. 1. Размеры самолёта (его длина) значительно меньше расстояния между городами. 2. Можно предположить, что движение пассажирского самолёта — поступательное. 3. Расстояние от диспетчера до самолёта в течение большей части полёта значительно больше размеров самолёта. Значит, самолёт можно принять за материальную точку.

Рассуждения Форма записи В этом случае возможно, что тело движется поступательно, когда его погружают в мензурку. Но этот признак в данном случае нельзя использовать, так как измеряют размеры тела. А материальная точка размеров не имеет. Случай б. В данном случае проводят измерение размеров тела, поэтому ими нельзя пренебречь, даже если тело помещают в мензурку, двигая его поступательно. Когда проводят измерение скорости движения Марса по орбите, пренебрегают его вращением вокруг оси, а наблюдатель находится от него на расстоянии, которое значительно больше радиуса планеты. (Дополнительные сведения найдите самостоятельно.) Случай в. Наблюдатель, измеряющий скорость движения Марса по его орбите, скорее всего, находится на Земле. Расстояние от наблюдателя превосходит размеры Марса весьма значительно. В последнем случае нельзя попасть впросак: материальная точка не имеет размеров, а массу имеет. В данном случае следует исходить из здравого смыла. Обычно размеры тела, массу которого определяют взвешиванием, сравнимы по значению с расстоянием до наблюдателя. Случай г. Взвешиваемое на весах тело обычно имеет размеры, сравнимые с расстоянием до исследователя, или проходит незначительные расстояния в данной процедуре, поэтому его нельзя считать материальной точкой.

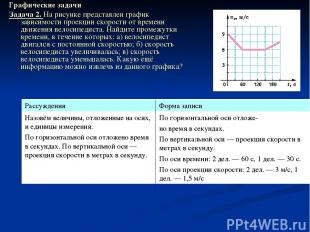
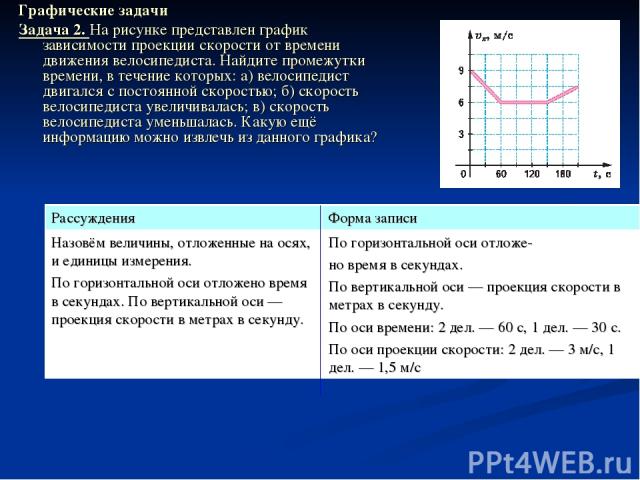
Графические задачи Задача 2. На рисунке представлен график зависимости проекции скорости от времени движения велосипедиста. Найдите промежутки времени, в течение которых: а) велосипедист двигался с постоянной скоростью; б) скорость велосипедиста увеличивалась; в) скорость велосипедиста уменьшалась. Какую ещё информацию можно извлечь из данного графика? Рассуждения Форма записи Назовём величины, отложенные на осях, и единицы измерения. По горизонтальной оси отложено время в секундах. По вертикальной оси — проекция скорости в метрах в секунду. По горизонтальной оси отложе- но время в секундах. По вертикальной оси — проекция скорости в метрах в секунду. По оси времени: 2 дел. — 60 с, 1 дел. — 30 с. По оси проекции скорости: 2 дел. — 3 м/с, 1 дел. — 1,5 м/с

Рассуждения Форма записи Найдём характерные точки на графике (то есть точки, лежащие на координатных осях, или те, в которых происходит «излом» линии) и сформулируем словами заключённую в них информацию. В момент t = 0 с проекция скорости vх0= 9 м/с. В момент t1 = 60 с проекция скорости vх1= 6 м/с. В момент t2 = 150 с проекция скорости vх2 = 6 м/с. В момент t3 = 210 с проекция скорости vх3 = 7,5 м/с. Эту же информацию можно представить в виде таблицы. (До- говоритесь между собой и согласуйте с учителем, в каком виде (словесном или табличном) вы будете представлять такую информацию при решении следующих задач.) Время, 0 60 150 210 t, с Проекция скорости, 9 6 6 7,5 vx, м/с

Рассуждения Форма записи Теперь нетрудно дать ответ на вопрос задачи. Этот ответ должен быть очень конкретным и содержать всю возможную информацию. а) Велосипедист двигался с постоянной скоростью 6 м/с в течение 90 с (от момента 60 с до момента 150 с). б) Его скорость увеличивалась с 6 м/с до 7,5 м/с в течение 60 с (от момента времени 150 с до момента времени 210 с). в) Его скорость уменьшалась с 9 м/с до 6 м/с в течение 60 с (в промежутке времени от начала движения до момента 60 с). Какую еще информацию можно извлечь, рассматривая эту ситуацию? Для этого будем формулировать новые вопросы. Так как скорость -величина векторная, то интересно знать, как она направлена? Так как в течение всего времени движения проекция скорости оставалась положительной, то движение велосипедиста происходило в одном направлении

Рассуждения Форма записи Теперь можно изобразить структурно-логическую схему задачи: указать направление векторов скорости велосипедиста в разные моменты времени, в системе отсчета, в которой рассматривается движение велосипедиста. Так как скорость велосипедиста на отдельных участках изменялась, то можно найти ускорение. С каким ускорением двигался велосипедист на разных участках движения?

Рассуждения Форма записи Так как ускорение векторная величина, то можно сформулировать следующий вопрос. Как направлен вектор ускорения на каждом этапе движения велосипедиста? Показать на структурно-логической схеме направления векторов ускорения Заштриховать на графике фигуры, площади которых, численно равны перемещению велосипедиста на каждом этапе его движения

Рассуждения Форма записи

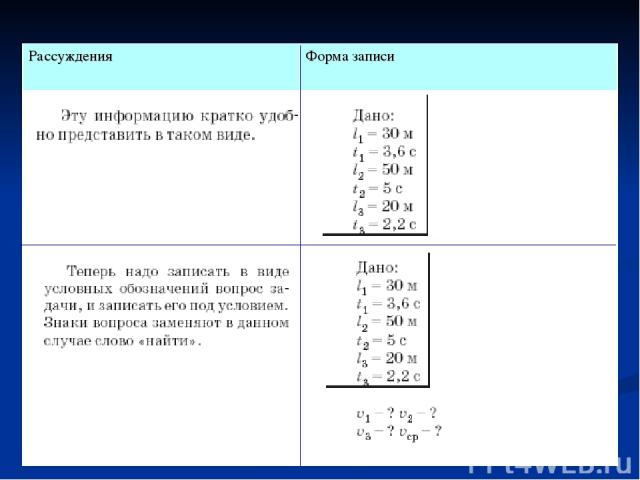
Рассчетные задачи. Задача 3.График бега спортсмена на стометровке таков: первые 30 м он пробежал за 3,6 с, следующие 50 м – за 5 с, а последние 20 м - за 2,2 с. Рассчитайте средние скорости спортсмена на каждом участке и на всем пути Рассуждения Форма записи

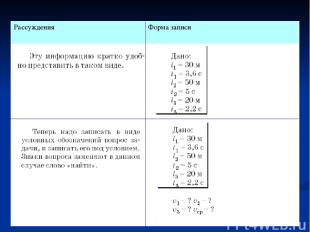
Рассуждения Форма записи

Рассуждения Форма записи

Пример подачи информации в визуальном и вербальном ряду

Готовятся к изданию Степанова Г.Н. Физика. 8 класс Степанова Г.Н. Методика преподавания физики 10-11 классы Степанова Г.Н. Физика. 9 класс Степанова Г.Н. Физика. 11 класс Степанова Г.Н. Методика преподавания физики 7-9 классы . Степанова Г.Н. Комплект рабочих тетрадей по физике. 7-11 классы