Презентация на тему: Треугольник Паскаля

Работа выполнена Бессоновой Марией ученицей 10 А класса МОУ СОШ № 1 г. Михайловска 2010 год 900igr.net

“Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике.” Мартин Гарднер

Треугольник Паскаля — арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля.

Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси. Имеет применение в теории вероятности и обладает занимательными свойствами.

Мартин Гарднер пишет в книге "Математические новеллы" (М., Мир, 1974): "Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике".

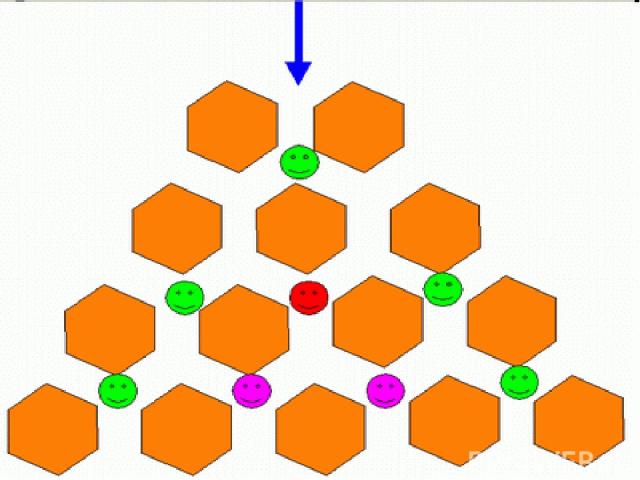
Предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смаликом, а тремя, соответственно, розовым. Это один из вариантов построения треугольника, предложенный Гуго Штейнгаузом в его классическом "Математическом калейдоскопе".

А еще проще объясняют устройство треугольника Паскаля слова: каждое число равно сумме двух расположенных над ним чисел. Все элементарно, но сколько в этом таится чудес.

На вершине треугольника стоит 1. Треугольник можно продолжать неограниченно. Он обладает симметрией относительно вертикальной оси, проходящей через его вершину. Вдоль диагоналей (насколько у треугольника могут быть диагонали, но не будем придираться, такая терминология встречается в публикациях), параллельных сторонам треугольника (на рисунке отмечены зелеными линиями) выстроены треугольные числа и их обобщения на случай пространств всех размерностей.

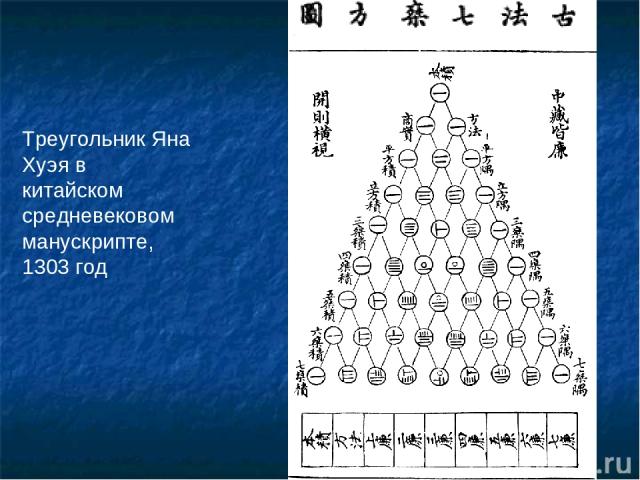
Треугольник Яна Хуэя в китайском средневековом манускрипте, 1303 год Первое упоминание треугольной последовательности биномиальных коэффициентов под названием meru-prastaara встречается в комментарии индийского математика X века Халаюдхи к трудам другого математика, Пингалы. Треугольник исследуется также Омаром Хайямом около 1100 года, поэтому в Иране эту схему называют треугольником Хайяма. В 1303 году была выпущена книга «Яшмовое зеркало четырёх элементов» китайского математика Чжу Шицзе, в которой был изображен треугольник Паскаля на одной из иллюстраций; считается, что изобрёл его другой китайский математик, Ян Хуэй (поэтому китайцы называют его треугольником Яна Хуэя). На титульном листе учебника арифметики, написанном в 1529 году Петром Апианом, астрономом из Ингольтштадского университета, также изображён треугольник Паскаля. А в 1653 году (в других источниках в 1655 году) вышла книга Блеза Паскаля «Трактат об арифметическом треугольнике».

Треугольник Яна Хуэя в китайском средневековом манускрипте, 1303 год

Второе число каждой строки соответствует её номеру. Третье число каждой строки равно сумме номеров строк, ей предшествующих. Третье число каждой строки является треугольным. Четвертое число каждой строки является тетраэдрическим. Сумма чисел n-й восходящей диагонали, проведенной через строку треугольника с номером n − 1, есть n-е число Фибоначчи: Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана. Сумма чисел n-й строки треугольника Паскаля равна 2 . Простые делители чисел треугольника Паскаля образуют симметричные самоподобные структуры. Если в треугольнике Паскаля все нечётные числа окрасить в чёрный цвет, а чётные - в белый, то образуется треугольник Серпинского.

1.http://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA_%D0%9F%D0%B0%D1%81%D0%BA%D0%B0%D0%BB%D1%8F 2. Фукс Д., Фукс М. Арифметика биномиальных коэффициентов // Квант. — 1970. — № 6. — С. 17-25. 3. Weisstein, Eric W. Pascal's Triangle (англ.) на сайте Wolfram MathWorld. 4. Абачиев С. К. Радужная фрактальность треугольника Паскаля  5. http://arbuz.uzpak.uz/u_treug.html