Презентация на тему: Сложение гармонических колебаний

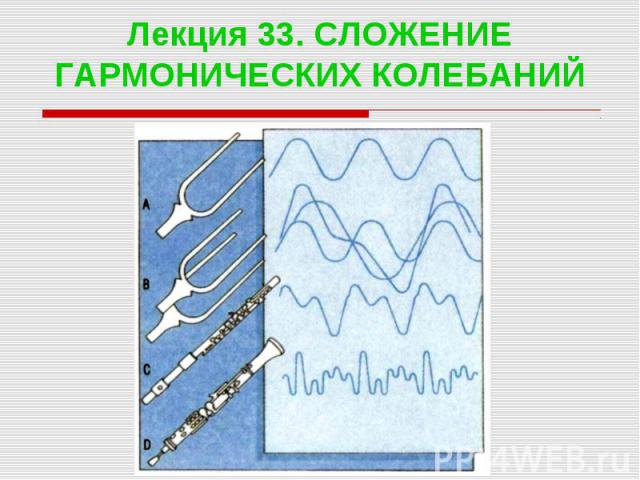
Лекция 33. СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

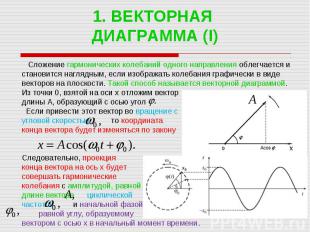
1. ВЕКТОРНАЯ ДИАГРАММА (I) Сложение гармонических колебаний одного направления облегчается и становится наглядным, если изображать колебания графически в виде векторов на плоскости. Такой способ называется векторной диаграммой. Из точки 0, взятой на оси x отложим вектор длины А, образующий с осью угол Если привести этот вектор во вращение с угловой скоростью то координата конца вектора будет изменяться по закону Следовательно, проекция конца вектора на ось x будет совершать гармонические колебания с амплитудой, равной длине вектора циклической частотой и начальной фазой равной углу, образуемому вектором с осью x в начальный момент времени.

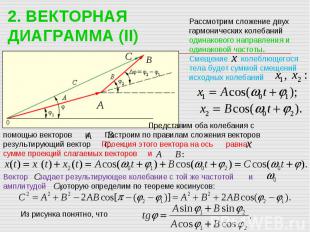
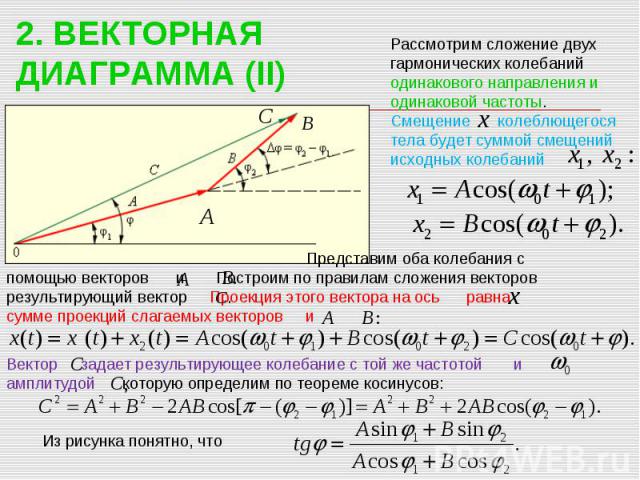
2. ВЕКТОРНАЯ ДИАГРАММА (II) Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты. Смещение колеблющегося тела будет суммой смещений исходных колебаний Представим оба колебания с помощью векторов и Построим по правилам сложения векторов результирующий вектор Проекция этого вектора на ось равна сумме проекций слагаемых векторов и Вектор задает результирующее колебание с той же частотой и амплитудой которую определим по теореме косинусов: Из рисунка понятно, что

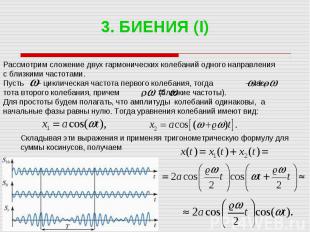
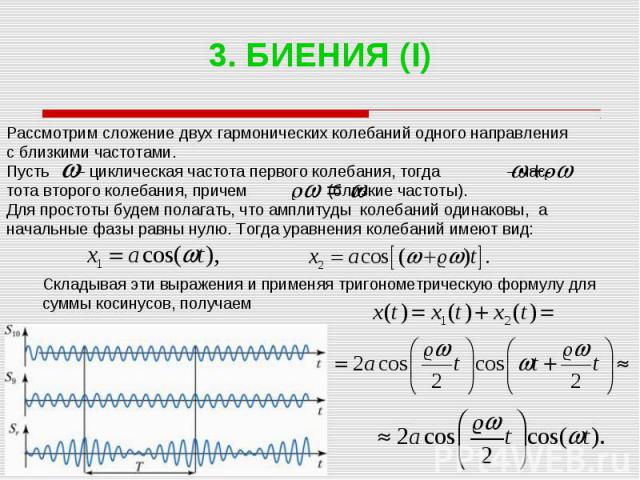
3. БИЕНИЯ (I) Рассмотрим сложение двух гармонических колебаний одного направления с близкими частотами. Пусть – циклическая частота первого колебания, тогда – час- тота второго колебания, причем (близкие частоты). Для простоты будем полагать, что амплитуды колебаний одинаковы, а начальные фазы равны нулю. Тогда уравнения колебаний имеют вид: Складывая эти выражения и применяя тригонометрическую формулу для суммы косинусов, получаем

4. БИЕНИЯ (II) Первый множитель в формуле изменяется значительно медленнее, чем второе, так как Это позволяет рассматривать результи-рующее колебание как гармоничес-кое с высокой частотой амплитуда которого пульсирует с низкой частотой Такое колебание называется биениями. Амплитуда биений определяется модулем выражения, стоящего перед гармонической функцией высокой частоты Амплитуда колеблется с частотой – частотой биений.

5. СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ Пусть частица участвует одновременно в двух взаимно перпендикулярных колебаниях одной частоты. Пусть колебания вдоль оси происходят с нулевой начальной фазой, а вдоль оси со сдвигом по фазе на Тогда уравнения колебаний примут вид: Чтобы получить уравнение траектории в явном виде исключим время Из первого уравнения следует, что Подставляя синус и косинус в формулу для получим: Уединяя иррациональность и возводя в квадрат, придем к уравнению которое представляет собой уравнение эллипса. Полуоси этого эллипса в общем случае не совпадают с осями координат.

6. ДВИЖЕНИЕ ПО ПРЯМОЙ Определим форму траектории результирующего колебания для некоторых частных случаев. Пусть В этом случае общее уравнение траектории принимает вид Движение является гармоническим колебанием вдоль прямой с амплитудой 2. Пусть В этом случае Траектория является прямой, лежа- щей во 2-м и 4-м квадрантах.

7. ДВИЖЕНИЕ ПО ЭЛЛИПСУ При общее уравнение траектории принимает вид Это уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний. При движение против часовой стрелки. При движение по часовой стрелке

8. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ Если то уравнение траектории Знак «+» в выражении для соответствует движению против часовой стрелки, знак «-» – движению по часовой стрелке. принимает вид При равенстве амплитуд эллипс вырождается в окружность. Это означает что равномерное движение по окружности радиуса с угловой скоростью может быть представлена как сумма двух взаимно перпендикулярных колебаний

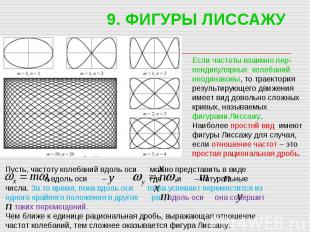
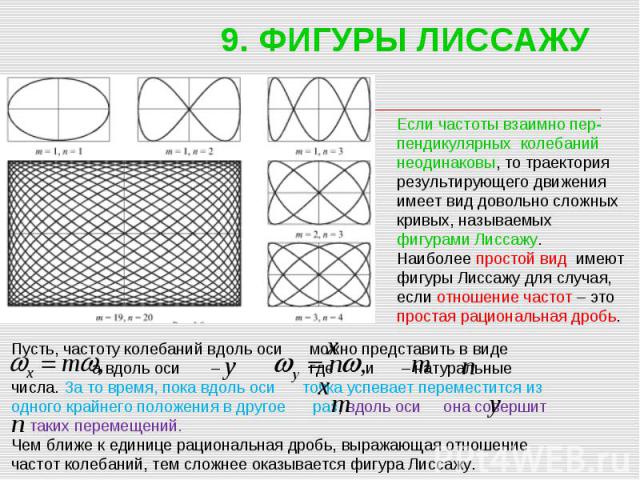
9. ФИГУРЫ ЛИССАЖУ Если частоты взаимно пер- пендикулярных колебаний неодинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. Наиболее простой вид имеют фигуры Лиссажу для случая, если отношение частот – это простая рациональная дробь. Пусть, частоту колебаний вдоль оси можно представить в виде а вдоль оси – где и – натуральные числа. За то время, пока вдоль оси точка успевает переместится из одного крайнего положения в другое раз, вдоль оси она совершит таких перемещений. Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу.