Презентация на тему: Принцип относительности в механике

Лекция 8 Тема: Принцип относительности в механике 1. Принцип относительности и преобразования Галилея. 2. Принцип относительности Эйнштейна. 3. Относительность временных интервалов. 4. Относительность пространственных интервалов. 5. Преобразования Лоренца 6. Пространственно-временной интервал. 7. Релятивистский импульс. Второй закон Ньютона. 8. Энергия частицы. Содержание лекции: Сегодня: * 900igr.net

1. Принцип относительности Галилея

Никакими механическими опытами, проводимыми в ИСО, нельзя установить, движется эта система отсчета прямолинейно и равномерно или покоится. любое механическое явление протекает одинаково во всех инерциальных системах отсчета (ИСО). Прямые и обратные преобразования Галилея

Преобразования Галилея позволяют по известным координатам и времени некоторого события в одной ИСО, найти координаты и время этого же события в другой ИСО, движущейся относительно первой с некоторой скоростью V. Уравнения классической механики инвариантны относительно преобразований Галилея, т. е вид уравнений не изменяется. Физические величины, которые при преобразованиях Галилея остаются неизменными, называются инвариантами преобразований Галилея.

Например, инвариантность второго закона Ньютона относительно преобразований Галилея проявляется в том, что вид этого уравнения сохраняется при переходе от неподвижной к движущейся СО: Консервативные силы взаимодействия также являются инвариантами. Эти два факта обеспечивают инвариантность всего второго закона Ньютона.

Пространственный интервал, т.е. расстояние между пространственными точками: Временной интервал:

Скорость относится к неинвариантным величинам: Классический закон сложения скоростей: Принцип относительности и преобразования Галилея отражают представления об абсолютном пространстве и абсолютном времени, которые лежат в основе классической механики.

2. Принцип относительности Эйнштейна.

В основе СТО Эйнштейна лежат два постулата: Принцип относительности Эйнштейна: все физические явления в ИСО протекают одинаково. Принцип постоянства скорости света в вакууме: скорость света в вакууме одинакова во всех системах отсчета и не зависит от движения источников и приемников света, т.е. является универсальной постоянной:

Скорость света в вакууме является не только универсальной постоянной. Оказывается, что она есть максимально возможная скорость движения в природе, т.е. никакой сигнал, никакое воздействие одного тела на другое не может распространяться со скоростью большей скорости света в вакууме. С этой точки зрения понятно, что предельная и максимальная скорость движения должна быть одинаковой во всех ИСО.

Следствия основных принципов теории относительности: 1. Относительность временных интервалов.

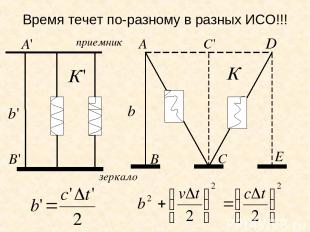
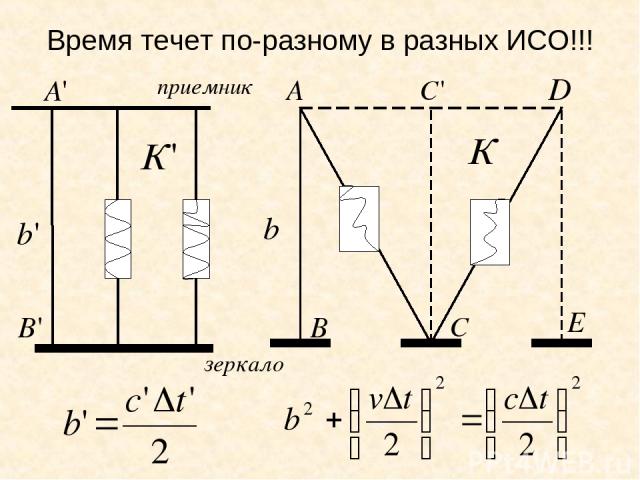
Время течет по-разному в разных ИСО!!!

Согласно принципу относительности, размеры перпендикулярные вектору скорости не изменяются, т.е. А согласно принципу постоянства скорости света:

Время, отсчитываемое по часам, движущимся вместе с объектом, называется собственным временем объекта t0. Движущиеся часы идут медленнее неподвижных. Т.О., не существует единого мирового времени. Время, его течение, понятие одновременности событий – относительны.

2. Относительность пространственных интервалов.

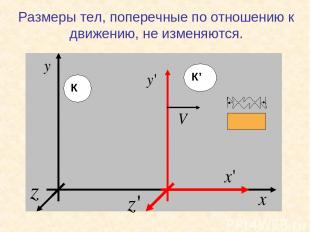
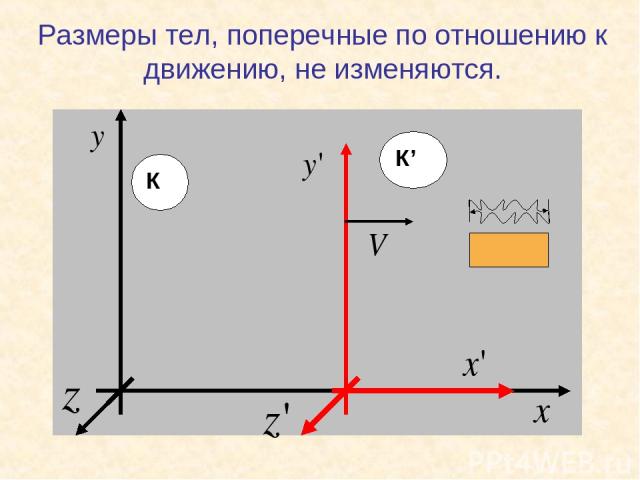
Размеры тел, поперечные по отношению к движению, не изменяются.

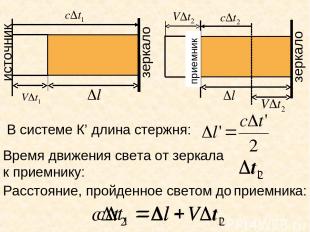
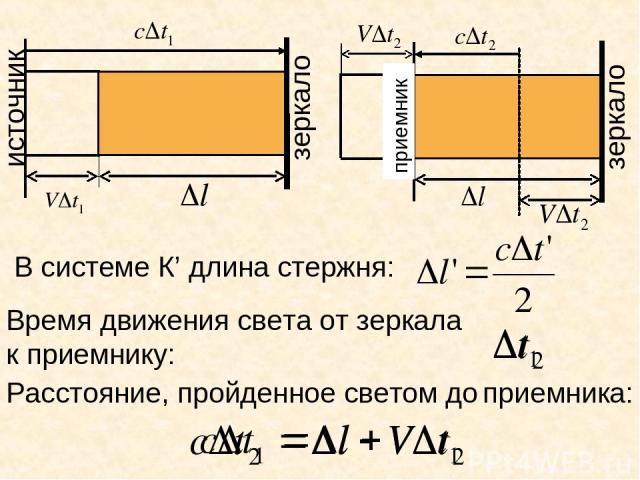
В системе К’ длина стержня: Время движения света до зеркала Расстояние, пройденное светом до зеркала зеркало зеркало источник приемник Время движения света от зеркала к приемнику: Расстояние, пройденное светом до приемника:

Общее время движения света до зеркала и обратно к приемнику: Тогда длина стержня в системе К будет: Заменяя t на t’, учитывая, что И вводя обозначение l’ = l, получим

Во всех системах отсчета длина тел уменьшается по сравнению с собственной. Это явление называется лоренцевым сокращением размеров тел в направлении движения.

5. Преобразования Лоренца

Зная как изменяются пространственные и временные интервалы при переходе от одной инерциальной системы отсчета к другой, можно получить релятивистские преобразования координат и времени (прямые преобразования Лоренца):

При малых по сравнению со скоростью света скоростях движения, т.е. V/c

3. Необходимо вводить релятивистский закон сложения скоростей: Если вместо движения частицы рассмотрим распространение света, т.е. u’ = c, тогда Скорость света одна и та же в различных ИСО (принцип постоянства скорости света).

6. Пространственно-временной интервал

Пусть в некоторой ИСО в точках А(x1, y1, z1) и В(x2, y2, z2) произошли в моменты времени t1 и t2 два события. При переходе в другую систему отсчета с помощью преобразований Галилея координаты точек А и В изменятся. Однако пространственный интервал Не изменяется и временной интервал

В релятивисткой механике инвариантность пространственных и временных интервалов относительно преобразований Лоренца не имеет места. Инвариантом в СТО является пространственно-временной интервал:

Два вида пространственно-временных интервалов между событиями: Времениподобные интервалы: действительные интервалы, для которых. Для событий, связанных такими интервалами, т.е. во всех системах время между событиями больше времени, в течение которого свет проходит расстояние между точками, в которых эти события произошли. Световой луч, испущенный из первой точки в момент первого события, может быть использован для инициирования второго события во второй точке. Времениподобные интервалы связывают такие события, между которыми существует или может существовать причинно-следственная связь.

2. Пространственно-подобные интервалы: мнимые интервалы, для которых. Для событий, связанных такими интервалами, т.е. событие во второй точке происходит раньше, чем туда прибудет свет, испущенный из первой точки в момент первого события. Поэтому причинно-следственная связь между такими событиями невозможна и эти события между собой абсолютно независимы.

7. Релятивистский импульс. Второй закон Ньютона.

Второй закон Ньютона инвариантен относительно преобразований Галилея. В области больших скоростей эти преобразования теряют силу и уступают место преобразованиям Лоренца. Релятивистский импульс: - Второй закон Ньютона

В релятивистском законе динамики в общем случае направления векторов ускорения тела и действующей силы не совпадают; нарушается и пропорциональность между величинами ускорения и силы. Два частных случая совпадения ускорения с направлением силы:

8. Энергия частицы.

Полная энергия в релятивистской механике имеет богатое содержание: 1) 2) В состоянии покоя V = 0 полная энергия не равна нулю (энергия покоя): Масса и энергия в любом теле представлены в пропорциональных количествах. Каждое изменение энергии покоя неизбежно сопровождается пропорциональным изменением его массы. Энергия покоя представляет собой внутреннюю энергию частицы или тела, не связанную с движением тела как целого и его взаимодействием с внешними силовыми полями.

В случае сложного тела, состоящего из многих частиц, его энергия покоя складывается из энергии покоя частиц, их кинетической энергии (обусловленной движением частиц относительно центра инерции тела) и потенциальной энергии взаимодействия частиц между собой. Потенциальная энергия частиц во внешнем поле в энергию покоя не включается, так же как и в полную энергию. Кинетическая энергия тела:

Связь полной энергии и импульса: Взятые друг от друга раздельно, энергия и импульс относительны, т.е. различны в разных СО. Однако взятые в виде комбинации образуют абсолютную характеристику состояния частицы, инвариантную относительно преобразований Лоренца.

Задача 1. Солнечная постоянная (плотность падающего на Землю потока энергии излучения Солнца) равна С = 1,4 кВт/м2. Определить массу Δm, которую теряет Солнце за один год. Решение: Земля находится от Солнца на расстоянии За время Δt на единицу площади падает энергия Умножая на площадь сферы радиусом L, получаем полную энергию, излученную Солнцем за время Δt: Эта энергия возникает в результате термоядерных реакций за счет уменьшения энергии покоя Солнца.

Следовательно, его масса за год уменьшится на величину За время своего существования (5 млрд. лет) Солнце потеряло в массе Учитывая, что масса Солнца равна потери массы на излучение составляют 0,03%.

Пример демонстрирует важный вывод СТО: в природе нет закона сохранения массы, есть лишь закон сохранения полной энергии. Закон сохранения массы возник в классической физике только потому, что кинетические энергии продуктов химических реакций были намного меньше их энергий покоя.

Частицы, для которых W = cp называются ультрарелятивистскими. Для них . Такие частицы способны к множественному рождению других частиц (если ультрарелятивистские частицы присутствуют в космических лучах, то при их столкновении с атомами атмосферы возникают ливни рожденных частиц ). Не утрачивает смысл при m = 0. Тогда W = cp и V = c. Т.е. частицы с m = 0 движутся со скоростью света. Эти скорости являются врожденными для них, изначальными. Представители – фотоны , нейтрино .

Задача 2. Элементарная частица, называемая нейтральным - мезоном ( 0) распадается на два фотона: Определить импульсы фотонов, если распавшийся пи-мезон покоился. Масса частицы Решение: Так как вначале пи-мезон покоился, полный импульс системы был равен нулю. Из закона сохранения импульсы фотонов равны по величине и направлены в противоположные стороны. Следовательно, равны и энергии фотонов Закон сохранения энергии в этой реакции:

1916 г. Эйнштейн, обобщая идеи СТО не НИСО создал теорию гравитации (ОТО): любой объект, обладающий энергией Е, будет подвержен действию гравитационного поля как если бы он имел гравитационную массу mg. Связь mg с энергией определяется: Масса фотона равна нулю, но в любом гравитационном поле он должен вести себя как частица с гравитационной массой

При движении фотона вблизи поверхности Земли вверх по вертикали на расстояние l фотон должен затратить часть своей энергии на совершение работы против сил тяжести: Соответственно первоначальная энергия фотона должна уменьшится на величину Значит, частота фотона в конце пути будет меньше на величину

Относительное уменьшение частоты фотона при распространении по вертикали было измерено в 1960 г. американскими учеными Паундом и Ребкой. В условиях опыта оно составило малую величину . Следовательно, перепад высот в опыте Паунда-Ребки составлял Эффект изменения частоты света при удалении от большой тяготеющей массы называется гравитационным красным смещением.

Лекция окончена Нажмите клавишу для выхода