Презентация на тему: Основы специальной теории относительности

Основы специальной теории относительности

Г.Н. Степанова. Физика-11, ч.1 стр. 130 – Введение§ 28 – знать:В чем проявляется относительность механического движенияПринцип относительности ГалилеяСуть и принцип опыта МайкельсонаПостулаты СТО§ 29 – знать: Смысл и формулы для кинематических следствий СТО

Специальная (или частная) теория относительности (СТО) представляет собой современную физическую теорию пространства и времени. Наряду с квантовой механикой, СТО служит теоретической базой современной физики и техники. СТО часто называют релятивистской теорией, а специфические явления, описываемые этой теорией, – релятивистскими эффектами. Эти эффекты наиболее отчетливо проявляются при скоростях движения тел, близких к скорости света в вакууме c ≈ 3·108 м/с.

Создатели СТО Специальная теория относительности была создана А. Эйнштейном (1905 г.). Предшественниками Эйнштейна, очень близко подошедшими к решению проблемы, были нидерландский физик Х. Лоренц и выдающийся французский физик А. Пуанкаре.Значительный вклад внесли Д. Лармор, Д.Фитцджеральд, математик Г. Минковский.

Альберт Эйнштейн (Einstein) (14.III.1879–18.IV.1955) Физик-теоретик, один из основателей современной физики. Родился в Германии, с 1893 жил в Швейцарии, в 1933 эмигрировал в США. В 1905 вышла в свет его первая серьезная научная работа, посвященная броуновскому движению: «О движении взвешенных в покоящейся жидкости частиц, вытекающем из молекулярно-кинетической теории». В том же году вышла и другая работа Эйнштейна «Об одной эвристической точке зрения на возникновение и превращение света». Вслед за Максом Планком он выдвинул предположение, что свет испускается и поглощается дискретно, и сумел объяснить фотоэффект. Эта работа была удостоена Нобелевской премии (1921).Наибольшую известность Эйнштейну все же принесла теория относительности, изложенная им впервые в 1905 году, в статье «К электродинамике движущихся тел».

Хендрик Антон Лоренц (Lorentz) (18.VII.1853–4.II.1898) Нидерландский физик-теоретик, создатель классической электронной теории. Работы в области электродинамики, термодинамики, оптики, теории излучения, атомной физики. Исходя из электромагнитной теории Максвелла–Герца и вводя в учение об электричестве атомистику, создал (1880–1909) классическую электронную теорию, основанную на анализе движений дискретных электрических зарядов. Вывел формулу, связывающую диэлектрическую проницаемость с плотностью диэлектрика, и зависимость показателя преломления вещества от его плотности (формула Лоренца–Лоренца), дал выражение для силы, действующей на движущийся заряд в магнитном поле (сила Лоренца), объяснил зависимость электропроводности вещества от теплопроводности, развил теорию дисперсии света. Для объяснения опыта Майкельсона–Морли выдвинул (1892) гипотезу о сокращении размеров тел в направлении их движения (сокращение Лоренца). В 1904 вывел формулы, связывающие между собой пространственные координаты и моменты времени одного и того же события в двух различных инерциальных системах отсчета (преобразования Лоренца). Подготовил переход к теории относительности.

Анри Пуанкаре (Poincare) (29.IV.1854–17.VII.1912) Французский математик и физик. Основные труды по топологии, теории вероятностей, теории дифференциальных уравнений, теории автоморфных функций, неевклидовой геометрии. Занимался математической физикой, в частности теорией потенциала, теорией теплопроводности, а также решением различных задач по механики и астрономии. В 1905 написал сочинения «О динамике электрона», в которой независимо от А. Эйнштейна развил математические следствия «постулата относительности».

Принцип относительности и преобразования Галилея. законы динамики одинаковы во всех инерциальных системах отсчета. Этот принцип означает, что законы динамики инвариантны (т. е. неизменны) относительно преобразований Галилея, которые позволяют вычислить координаты движущегося тела в одной инерциальной системе (K), если заданы координаты этого тела в другой инерциальной системе (K'). В частном случае, когда система K' движется со скоростью υ вдоль положительного направления оси x системы K преобразования Галилея имеют вид: x = x' +  υxt,   y = y',   z = z',   t = t'.В начальный момент оси координат обеих систем совпадают.

Принцип относительности и преобразования Галилея. Следствие преобразований Галилея - закон преобразования скоростей при переходе от одной системы отсчета к другой: υx =  υ'x +  υ,    υy =  υ'y,    υz =  υ'z.Ускорения тела во всех инерциальных системах оказываются одинаковыми. Следовательно, уравнение движения классической механики не меняет своего вида при переходе от одной инерциальной системы к другой.

Постулаты СТО В основе специальной теории относительности лежат два постулата (или принципа), сформулированные Эйнштейном в 1905 г.Эти принципы являются обобщением всей совокупности опытных фактов.

Принцип относительности Эйнштейна: все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. Это означает, что во всех инерциальных системах физические законы (не только механические) имеют одинаковую форму.

Принцип постоянства скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета. Скорость света в СТО занимает особое положение. Это предельная скорость передачи взаимодействий и сигналов из одной точки пространства в другую.

Принцип соответствия Н.Бора новая теория (СТО) не отвергла старую классическую механику Ньютона, а только уточнила пределы ее применимости. Такая взаимосвязь между старой и новой, более общей теорией, включающей старую теорию как предельный случай, носит название принципа соответствия.

Опыты Майкельсона и Морли Майкельсон (Michelson) Альберт (19.XII.1852–9.V.1931).Американский физик. В 1878–82 и 1924–26 провел измерения скорости света, долгое время остававшиеся непревзойденными по точности. В 1881 экспериментально доказал и совместно с Э. У. Морли (1885–87) подтвердил с большой точностью независимость скорости света от скорости движения Земли.Морли (Morley) Эдвард Уильямс (29.I.1839–1923) Американский физик. Наибольшую известность получили его работы в области интерферометрии, выполненные совместно с Майкельсоном. В химии же высшим достижением Морли было точное сравнение атомных масс элементов с массой атома водорода, за которое ученый был удостоен наград нескольких научных обществ.

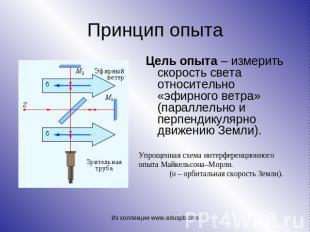
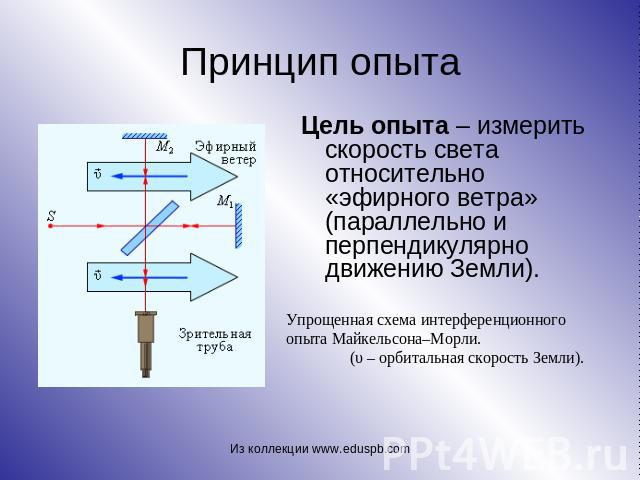
Принцип опыта Цель опыта – измерить скорость света относительно «эфирного ветра» (параллельно и перпендикулярно движению Земли). Упрощенная схема интерференционного опыта Майкельсона–Морли. (υ – орбитальная скорость Земли).

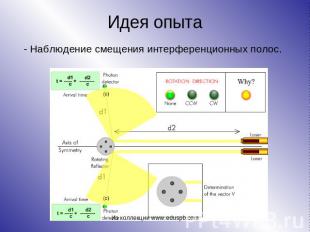
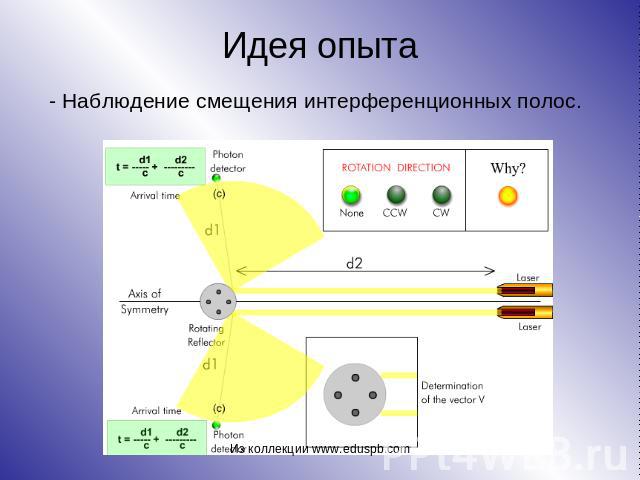
Идея опыта - Наблюдение смещения интерференционных полос.

Преобразования Лоренца Кинематические формулы преобразования координат и времени в СТО называются преобразованиями Лоренца. Они были предложены в 1904 году еще до появления СТО как преобразования, относительно которых инвариантны уравнения электродинамики. Для случая, когда система K' движется относительно K со скоростью υ вдоль оси x, преобразования Лоренца имеют вид:

Относительность одновременности события, являющиеся одновременными в одной ИСО, неодновременны в другой ИСО, движущейся относительно первой

Относительность промежутков времени. Моменты наступлений событий в системе K' фиксируются по одним и тем же часам C, а в системе K – по двум синхронизованным пространственно-разнесенным часам C1 и C2. Система K' движется со скоростью υ в положительном направлении оси x системы K.

Относительность промежутков времени.

Пример если космонавты отправляются к звездной системе (и обратно), находящейся на расстоянии 500 световых лет от Земли, со скоростью v=0,9999c, то на это потребуется по их часам 14,1 года; в то время как на Земле пройдет 10 веков

Относительность расстояний Измерение длины движущегося стержня

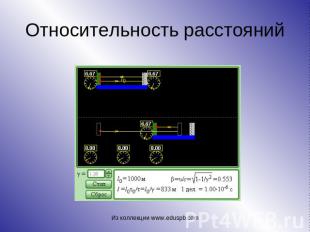
Относительность расстояний

Г.Н. Степанова. Физика-11, ч.1 § 30, 31 – знать:Формулу сложения скоростей и ее смысл.Формулу релятивистского импульсаФормулы полной энергии и энергии покояСвязь энергии и импульсаПонимать задачи и границы применимости СТО, принцип соответствияВ помощь: Таблица «Подведем итоги» на стр. 146.

Сложение скоростей Эти соотношения выражают релятивистский закон сложения скоростей для случая, когда частица движется параллельно относительной скорости систем отсчета K и K'. При υ << c релятивистские формулы переходят в формулы классической механики:

Сложение скоростей Если в системе K' вдоль оси x' распространяется со скоростью u'x = c световой импульс, то для скорости ux импульса в системе K получим В любом случае выполняется условие ux ≤ с. Например, пусть u’x = с и υ = c. Тогда:

Импульс в СТО Уравнения классической механики Ньютона оказались неинвариантными относительно преобразований Лоренца, и поэтому СТО потребовала пересмотра и уточнения законов механики.В основу такого пересмотра Эйнштейн положил требования выполнимости закона сохранения импульса и закона сохранения энергии в замкнутых системах. Для этого оказалось необходимым изменить определение импульса тела. Релятивистский импульс тела с массой m, движущегося со скоростью записывается в виде

Масса в СТО Масса m, входящая в выражение для импульса, есть фундаментальная характеристика частицы, не зависящая от выбора инерциальной системы отсчета, а, следовательно, и от скорости ее движения.(Во многих учебниках прошлых лет ее было принято обозначать буквой m0 и называть массой покоя. Кроме того, вводилась так называемая релятивистская масса, зависящая от скорости движения тела. Современная физика постепенно отказывается от этой терминологии).

Динамика СТО Основной закон релятивистской динамики материальной точки записывается так же, как и второй закон Ньютона, но только в СТО под понимается релятивистский импульс частицы:

Энергия в СТО Вычисление кинетической энергии приводит к следующему выражению: Эйнштейн интерпретировал первый член в правой части этого выражения как полную энергию E движущийся частицы, а второй член как энергию покоя.

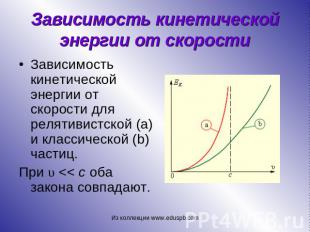
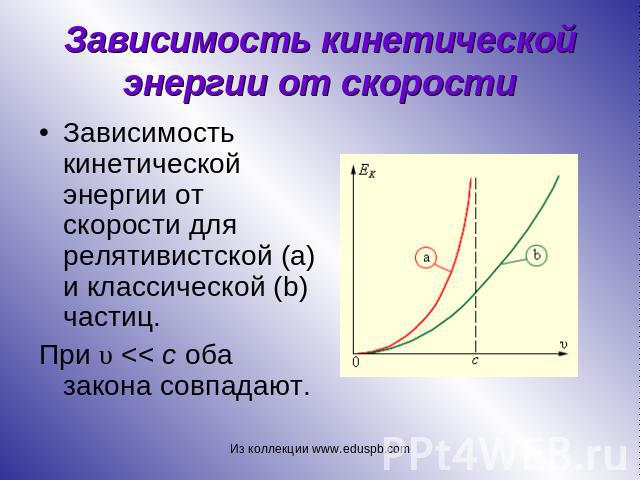
Зависимость кинетической энергии от скорости Зависимость кинетической энергии от скорости для релятивистской (a) и классической (b) частиц. При υ << c оба закона совпадают.

Связь массы и энергии Утверждение о том, что находящаяся в покое масса m содержит огромный запас энергии получило разнообразные практические применения, включая использование ядерной энергии. Если масса частицы или системы частиц уменьшилась на Δm, то при этом должна выделиться энергия ΔE = Δm·c2. Многочисленные прямые эксперименты дают убедительные доказательства существования энергии покоя.

Связь массы и энергии Закон пропорциональности массы и энергии является одним из самых важных выводов СТО. Масса и энергия являются характеристиками материальных объектов. Масса тела характеризует его инертность, а также способность тела вступать в гравитационное взаимодействие с другими телами. Важнейшим свойством энергии является ее способность превращаться из одной формы в другую в эквивалентных количествах при различных физических процессах. Формула Эйнштейна выражает фундаментальный закон природы, который принято называть законом взаимосвязи массы и энергии.

Связь энергии и импульса Между полной энергией, энергией покоя и импульсом существует следующая связь: Отсюда следует, что для покоящихся частиц (p = 0) E = E0 = mc2.

Безмассовые частицы Т.о. частица может иметь энергию и импульс, но не иметь массы (m = 0). Такие частицы называются безмассовыми. Для безмассовых частиц связь между энергией и импульсом выражается простым соотношением Е = pc. К безмассовым частицам относятся фотоны – кванты электромагнитного излучения и, возможно, нейтрино.Безмассовые частицы не могут существовать в состоянии покоя, во всех инерциальных системах отсчета они движутся с предельной скоростью c.

Подведем итоги

Задание 1 Два автомобиля движутся в противоположных направлениях со скоростями υ1 и υ2 относительно поверхности Земли. Чему равна скорость света от фар первого автомобиля в системе отсчета, связанной с другим автомобилем? c + (υ1 + υ2) c - (υ1 – υ2) c – (υ1 + υ2) c – (υ1 – υ2) c

Панель дома массой 200 кг поднята на высоту 10 м. Как изменится при этом его масса? Не изменится Увеличится на 0,22∙10–12 кгУменьшится на 0,22∙10–12 кг Для решения задачи не хватает данных

Опыты по наблюдению спектра водорода, находящегося в спектральной трубке, выполнялись дважды. Первый раз на Земле, второй раз в космическом корабле, движущемся относительно Земли с постоянной скоростью. Наблюдаемые спектры одинаковы существенно различны сходны, но все спектральные линии сдвинуты друг относительно друга

Рассчитайте отношение времени τ в системе отсчета, движущейся со скоростью υ = 1,5∙108 м/с относительно лабораторной системы отсчета, к собственному времени τ 0.

Найдите скорость υ частицы, которой потребовалось бы на 2 года больше, чем световому импульсу, чтобы пройти расстояние в 6,0 световых лет до далекой звезды. Скорость частицы выразите в долях скорости света c.