Презентация на тему: Механические передачи зацепления

Тема 6 Механические передачи зацепления

План лекции Виды зубчатых передач. Основные характеристики зубчатых передач. Геометрия и кинематика эвольвентного зубчатого зацепления. Материалы и допускаемые напряжения. Допускаемые контактные напряжения. Расчет зубчатого зацепления на контактную прочность. . Расчет зубьев на изгиб. Проектировочный расчет на контактную выносливость. Зубчатые редукторы. Червячные передачи. Общие сведения. Классификация червячных передач. Верхнее и нижнее расположение червяка. Геометрия и кинематика червячного зацепления. Расчет червячного зацепления на контактную прочность. Расчет открытых червячных передач. Конструкции червяков и червячных колес. Цепные передачи. Основные характеристики цепных передач, устройство и область применения. Основные геометрические параметры. Разрушающая нагрузка. Критерии работоспособности цепных передач. Передача винт-гайка. Устройство и назначение передач винт-гайка. Силовые соотношения в винтовой паре. Привод винтовой передачи. Критерии работоспособности. Методика расчета передачи. Грузовой винтовой механизм. Расчет винтов и гаек передач на прочность.

Виды цилиндрических зубчатых передач Цилиндрические зубчатые передачи передают вращающий момент между параллельными валами. Прямозубые колёса (около 70%) применяют при невысоких и средних скоростях, когда динамические нагрузки от неточности изготовления невелики, в планетарных, открытых передачах, а также при необходимости осевого перемещения колёс.

Косозубые колёса (более 30%) имеют большую плавность хода и применяются для ответственных механизмов при средних и высоких скоростях. Косозубые колёса (более 30%) имеют большую плавность хода и применяются для ответственных механизмов при средних и высоких скоростях. Шевронные колёса имеют достоинства косозубых колёс плюс уравновешенные осевые силы и используются в высоконагруженных передачах. Колёса внутреннего зацепления вращаются в одинаковых направлениях и применяются обычно в планетарных передачах. Выбор параметров цилиндрических зубчатых передач обусловлен конструктивными и технологическими условиями.

Передаточное отношение U определяется соотношением угловых скоростей (ω) или частот вращения (n) ведомого и ведущего колёс Передаточное отношение U определяется соотношением угловых скоростей (ω) или частот вращения (n) ведомого и ведущего колёс U = ω1 / ω2 = n1 / n2. Здесь и далее индексы 1 и 2 расставлены в порядке передачи механической энергии 1- ведущее (шестерня), 2- ведомое (колесо). Учитывая, что в зацепление входят колёса с одинаковым модулем (, можно задавшись числом зубьев шестерни Z1 найти число зубьев колеса Z2 = U * Z1. Передаточное число U ограничено габаритами зубчатой передачи.

Основные характеристики зубчатых передач Расчетная окружная скорость м/с цилиндрической зубчатой передачи Конической передачи где - угловая скорость зубчатого колеса, n- частота вращения зубчатого колеса, мин-1 dw- начальный диаметр цилиндрического зубчатого колеса, м dwm- начальный средний диаметр конического зубчатого колеса

Учитывая, что скорость точек начальных окружностей, находящихся в зацеплении зубчатых колес, одинаково, имеем Учитывая, что скорость точек начальных окружностей, находящихся в зацеплении зубчатых колес, одинаково, имеем Выражая диаметр через модуль зацепления и соответствующее число зубов, получаем Отсюда передаточное отношение пары зубчатых колес (для одноступенчатой передачи) где T1 и T2 - крутящий момент ведущего и ведомого колеса . Отношение числа зубьев Z2 колеса и числа зубьев Z1, шестерни называют передаточным числом зубчатой передачи .

Окружная сила цилиндрической зубчатой передачи определяется по формуле Окружная сила цилиндрической зубчатой передачи определяется по формуле Окружная сила конической зубчатой передачи определяется по формуле

Геометрия эволентного зубчатого зацепления Модуль зубьев m m = p/π = d/z Высота зуба h h = 2,25m 3. Высота головки зуба ha ha = m 4. Высота ножки зуба hf hf = 1,25m Диаметр делительной окружности d d = mz

Модуль зубьев m Модуль зубьев m m = p/π = d/z Высота зуба h h = 2,25m 3. Высота головки зуба ha ha = m 4. Высота ножки зуба hf hf = 1,25m Диаметр делительной окружности d d = mz

10. Шаг зубьев p 10. Шаг зубьев p p =π/m 11. Толщина зуба st st = 0,5p 12. Ширина впадины e e = 0,5p 13. Ширина венца зубчатого колеса (длина зуба) b b ≈ (6...8)m

Материалы и допускаемые напряжения Зубчатые колеса изготовляют из сталей, чугуна и неметаллических материалов. Колеса из неметаллических материалов имеют небольшую массу и не корродируют, а передачи с ними бесшумны в работе. Но невысокая прочность материалов и, как следствие, большие габари­ты передачи и сравнительно высокая стоимость изготовления колес ограничива­ют их применение в силовых механизмах. Чугунные зубчатые колеса дешевле стальных, их применяют в малонагруженных открытых передачах. Они имеют малую склонность к заеданию и хорошо работают при бедной смазке, но не выдерживают ударных нагрузок.

Допускаемые напряжения. Допускаемые напряжения изгиба при расчете на выносливость определяют по формуле Где σFlim — предел выносливости зубьев, соответствующий заданному (установленному) числу циклов нагружений; SF— коэффициент безопасности (допускаемый запас прочности); YS= 1,08—0,16lgm— коэффициент, учитывающий влияние абсолютных размеров зубьев; KxF=( 1 — 8,3X 10-5)da—то же, для колес (da — диаметр вершин колеса, мм; m — модуль, мм); YR — коэффициент, учитывающий влияние шероховатости поверхности (при полировании переходной поверхности равен 1.05÷1,2).

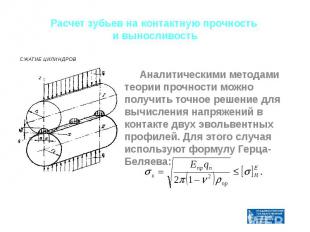
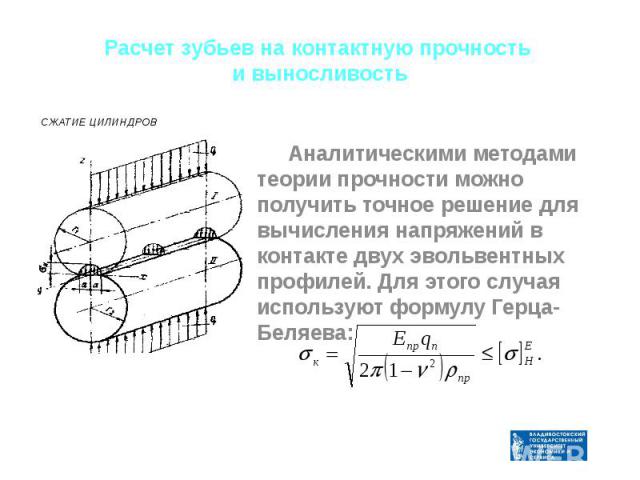
Расчет зубьев на контактную прочность и выносливость Аналитическими методами теории прочности можно получить точное решение для вычисления напряжений в контакте двух эвольвентных профилей. Для этого случая используют формулу Герца-Беляева:

Здесь Епр – приведённый модуль упругости материалов шестерни и колеса Здесь Епр – приведённый модуль упругости материалов шестерни и колеса Епр = 2 Е1 Е2 / ( Е1 + Е2), пр – приведённый радиус кривизны зубьев 1/ пр = 1/ 1 1/ 2, 1,2 = 0,5dW 1,2 sin W , - коэффициент Пуассона, qn - удельная погонная нормальная нагрузка, [ ]HE - допускаемые контактные напряжения с учётом фактических условий работы.

Расчёт зубьев на контактную выносливость для закрытых передач (длительно работают на постоянных режимах без перегрузок) выполняют как проектировочный. В расчёте задаются передаточным отношением, которое зависит от делительных диаметров и определяют межосевое расстояние Аw (или модуль m), а через него и все геометрические параметры зубьев. Для открытых передач контактные дефекты не характерны и этот расчёт выполняют, как проверочный, вычисляя контактные напряжения и сравнивая их с допускаемыми. Расчёт зубьев на контактную выносливость для закрытых передач (длительно работают на постоянных режимах без перегрузок) выполняют как проектировочный. В расчёте задаются передаточным отношением, которое зависит от делительных диаметров и определяют межосевое расстояние Аw (или модуль m), а через него и все геометрические параметры зубьев. Для открытых передач контактные дефекты не характерны и этот расчёт выполняют, как проверочный, вычисляя контактные напряжения и сравнивая их с допускаемыми.

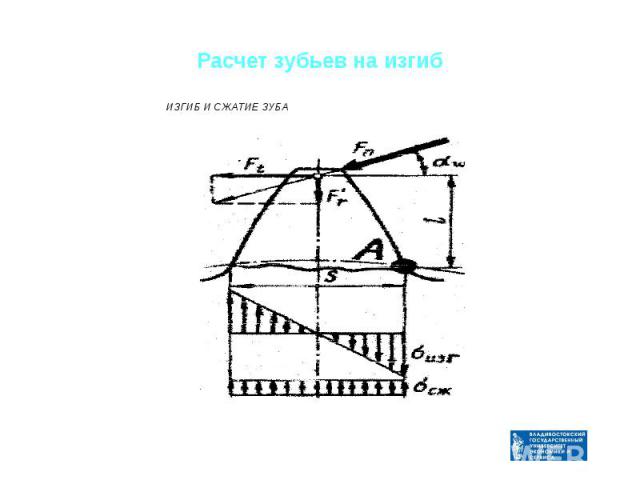
Расчет зубьев на изгиб

Напряжения сжатия вычитаются из напряжений изгиба. Учитывая, что напряжения изгиба в консольной балке равны частному от деления изгибающего момента Mизг на момент сопротивления корневого сечения зуба W, а напряжения сжатия это сила Fr, делённая на площадь корневого сечения зуба, получаем: Напряжения сжатия вычитаются из напряжений изгиба. Учитывая, что напряжения изгиба в консольной балке равны частному от деления изгибающего момента Mизг на момент сопротивления корневого сечения зуба W, а напряжения сжатия это сила Fr, делённая на площадь корневого сечения зуба, получаем: . Здесь b – ширина зуба, m – модуль зацепления, YH – коэффициент прочности зуба.

Зубчатые редукторы Редуктором называют механизм, состоящий из зубчатых или червячных передач, выполненный в виде отдельного агре­гата и служащий для передачи вращения от вала двигателя к валу рабочей машины. Назначение редуктора — понижение угловой скорости и соот­ветственно повышение вращающего момента ведомого вала по сравнению с ведущим. Редуктор состоит из корпуса (литого чугунного или свар­ного стального), в котором помещают элементы передачи — зубчатые колеса, валы, подшипники и т. д.

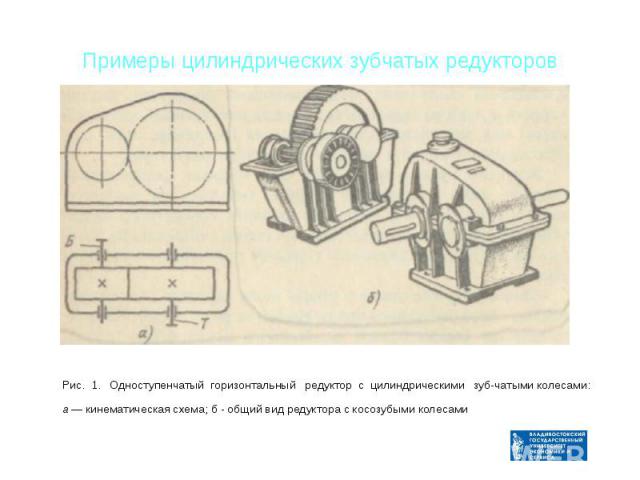
Примеры цилиндрических зубчатых редукторов Рис. 1. Одноступенчатый горизонтальный редуктор с цилиндрическими зуб­чатыми колесами: а — кинематическая схема; б - общий вид редуктора с косозубыми колесами

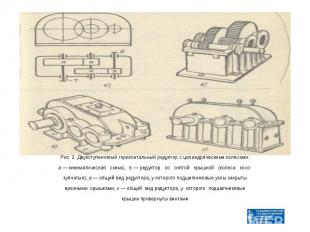
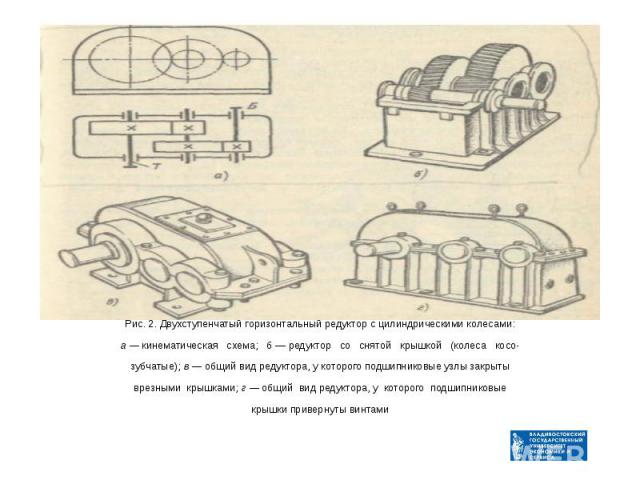
Рис. 2. Двухступенчатый горизонтальный редуктор с цилиндрическими колесами: а — кинематическая схема; б — редуктор со снятой крышкой (колеса косо- зубчатые); в — общий вид редуктора, у которого подшипниковые узлы закрыты врезными крышками; г — общий вид редуктора, у которого подшипниковые крышки привернуты винтами

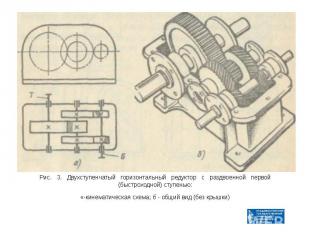
Рис. 3. Двухступенчатый горизонтальный редуктор с раздвоенной первой (быстроходной) ступенью: «-кинематическая схема; б - общий вид (без крышки)

Червячные передачи и передачи винт-гайка Основы проектирования червячных передач и винтовой передачи (винт-гайка) рассмотрены в теме 3 данной презентации.

Цепные передачи Основные характеристики цепных передач, устройств и область применения Рис.1. Схема цепной передачи

Передача (рис. 1) состоит обычно из ведущей 1 и ведомой 2 звездочек, связанных между собой приводной цепью (в машиностроении применяют также грузовые и тяговые цепи). Их применяют в качестве ступеней в приводах стационарных механизмов и машин (станках, роботах, сельскохозяйственной, транспортной технике и др.). Передача (рис. 1) состоит обычно из ведущей 1 и ведомой 2 звездочек, связанных между собой приводной цепью (в машиностроении применяют также грузовые и тяговые цепи). Их применяют в качестве ступеней в приводах стационарных механизмов и машин (станках, роботах, сельскохозяйственной, транспортной технике и др.). Числа зубьев z1 и z2 звездочек выби­рают из условия обеспечения минималь­ных габаритов и более плавного хода цепи. Расстояние а между осями звездочек (см. рис. 1) также влияет на работо­способность цепи, так как оно определяет частоту нагружения шарниров. При малом а цепь быстро изнашивается, а при большом а ведомая ветвь начинает колебать­ся из-за сильного провисания.

На практике стремятся к тому, чтобы На практике стремятся к тому, чтобы а=(30>50)t. Минимальное значение а ограничивают обхватом цепи (amin≥120°): при i≤3 amin = 0,5(d1+ d2) + (30÷50) мм; при i>3 Потребное число звеньев цепи (длина цепи в шагах) определяется по предва­рительно выбранным значениям a, t, z1 и z2: Для обеспечения нормального провиса­ния ведомой ветви цепи межосевое рас­стояние уменьшают на 0,2—0,4%.

Критерии работоспособности цепных передач Износ шарниров в процессе эксплуатации — типичный вид поврежде­ния цепей быстроходных закрытых и полузакрытых передач станков, двигателей и оборудования общего машиностроения. Усталостное разрушение элементов цепи вызывается переменными напряже­ниями от внешней нагрузки, сил инерции и ударных нагрузок, обусловленных вну­тренней динамикой цепного привода. Разрушению часто предшествует контактная коррозия, развивающаяся на стенках отверстий пластин и на поверхностях роликов и осей.

При скоростях vц>15 м/с возрастают ударные нагрузки в передаче, и даже при сравнительно небольших нагрузках может происходить раскалывание роликов и ослабление прессовых соединений вали­ков и втулок с пластинками. При скоростях vц>15 м/с возрастают ударные нагрузки в передаче, и даже при сравнительно небольших нагрузках может происходить раскалывание роликов и ослабление прессовых соединений вали­ков и втулок с пластинками. Таким образом, износостойкость и прочность цепей являются основными критериями работоспособности передач.

Контрольные вопросы 1.Виды зубчатых передач? 2.Основные характеристики зубчатых передач? 3.Как определяются контактные напряжения? 4. Как вычисляются напряжения сжатия? 5.Основные характеристики цепных передач? 6.Критерии работоспособности цепных передач? 7. Как рассчитывают зубья на контактную прочность и выносливость?