Презентация на тему: Импульс тела и импульс силы

Импульс тела и импульс силы

Положим на стол теннисный шарик. Если на него подуть, то шарик немного откатится в сторону. Если подуть сильнее, то шарик откатится дальше. Такого же результата можно достичь, если дуть не сильно, но более длительное время. Другими словами, результат действия силы на тело зависит не только от самой силы, но и от времени ее действия.

Произведение силы на время ее действия называется импульсом силы

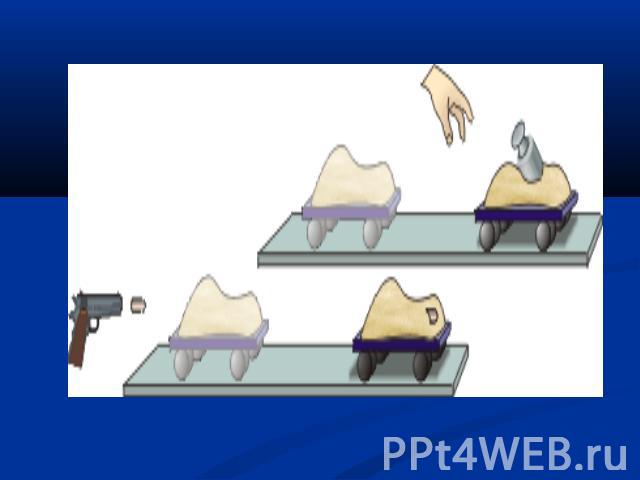
Вообразим, что у нас есть тележка с песком, стоящая на рельсах. Выстрелим из пистолета в тележку так, чтобы пуля застряла в песке. В результате тележка покатится по рельсам. Остановим ее и возьмем тяжелую гирю. Пронося ее над тележкой с небольшой скоростью, уроним на песок. После нескольких тренировок гирю можно уронить так, чтобы тележка двигалась с такой же скоростью, как и после выстрела из пистолета. В этом случае говорят, что пуля и гиря передали тележке одинаковое количество движения.

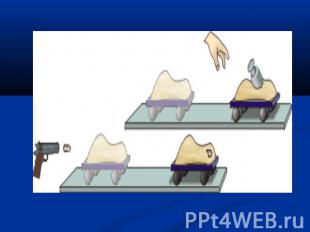
Пуля имела маленькую массу, но большую скорость. Гиря же имела маленькую скорость, но большую массу. Следовательно, количество движения тела зависит от его массы и скорости.

Количеством движения или импульсом тела называют произведение массы тела на вектор его скорости:

Поскольку скорость – векторная величина, а масса – положительный скаляр, то импульс тела, mv – вектор, сонаправленный с вектором скорости.

Закон сохранения импульса Подставим в формулу второго закона Ньютона формулу определения ускорения. В результате получим:

что в левой части равенства мы получили уже знакомую нам величину FDt – импульс силы. В правой части равенства тоже стоят знакомые нам величины: mv – конечный импульс и mv0 – начальный импульс тела. Разность mv – mv0 представляет собой изменение импульса тела. Поэтому полученную нами формулу мы прочтем так: импульс силы равен изменению импульса тела.

Рассмотрим два взаимодействующих тела, например, бильярдные шары. Запишем для них формулу третьего закона Ньютона F1 = – F2

Подставив два последних равенства в формулу третьего закона Ньютона и проведя преобразования, получим: Это утверждение называют законом сохранения импульса: сумма импульсов тел до взаимодействия равна сумме их импульсов после взаимодействия. Однако закон справедлив лишь в том случае, если рассматриваемые тела взаимодействуют только друг с другом.

Быстро летящие бильярдные шары можно приблизительно считать взаимодействующими только друг с другом. Поэтому на чертеже выполяется векторное равенство: 5 м/с = 3 м/с + 4 м/с .

Реактивное движение Реактивным движением называют движение тела, возникающее при отделении от него некоторой его части.