Презентация на тему: Электромагнитные волны

Лекция 4. Электромагнитные волны 900igr.net

Лекция 4. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ 4.1 Генерация ЭМВ Сегодня: * 4.2 Дифференциальное уравнение ЭМВ 4.3 Экспериментальное исследование ЭМВ 4.4 Энергия и импульс ЭМП

4.1 Генерация ЭМВ Максвелл Джеймс Клерк (1831 – 1879) – английский физик, член Эдинбургского (1855) и Лондонского (1861) королевских обществ, первый профессор экспериментальной физики в Кембридже. Под его руководством создана известная Кавендишская лаборатория, которую он возглавлял до конца своей жизни. Самым большим научным достижением Максвелла является созданная им теория электромагнитного поля, которую он сформулировал в виде системы нескольких уравнений (уравнения Максвелла), выражающих все основные закономерности электромагнитных явлений. В своей теории Максвелл дал определение электромагнитного поля и предсказал новый важный эффект: существование в свободном пространстве электромагнитных волн и их распространение в пространстве со скоростью света. Последнее дало ему основание считать свет одним из видов электромагнитного излучения.

Герц Генрих Рудольф (1857 – 1894) – немецкий физик. Окончил Берлинский университет (1880 г.) и был ассистентом у Г. Гельмгольца. В 1885 – 89 гг. – профессор Высшей технической школы в Карлсруэ. В 1887 г. в работе «Об очень быстрых электрических колебаниях» предложил удачную конструкцию генератора электромагнитных колебаний (вибратор Герца) и метод их обнаружения с помощью резонанса (резонатор Герца). Экспериментально доказал существование электромагнитных волн, распространяющихся в свободном пространстве, предсказанных теорией Максвелла. Экспериментируя с электромагнитными волнами, наблюдал их отражение, преломление, интерференцию, поляризацию. Развивая теорию Максвелла, он придал уравнениям электродинамики форму, которая хорошо обнаруживала полную взаимосвязь между электрическими и магнитными явлениями.

В колебательном контуре, образованном конденсатором С и катушкой L, электрическое поле сосредоточено в зазоре между обкладками, а магнитное – внутри катушки. В окружающем конденсатор и катушку пространстве поля практически равны нулю…

Вибратор Герца Вибратор R – разрядник; Т - газоразрядная трубка; D – дроссели. Резонатор Движущийся с ускорением электрический заряд испускает электромагнитные волны.

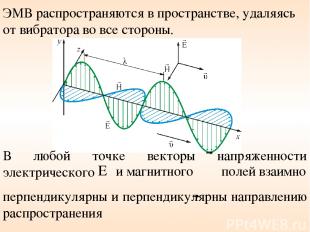
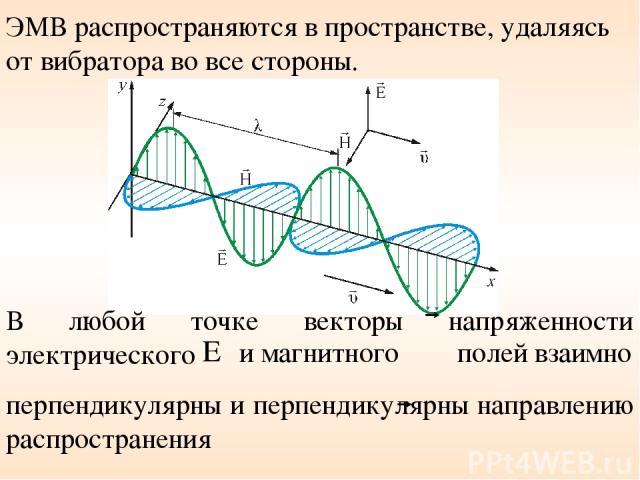
ЭМВ распространяются в пространстве, удаляясь от вибратора во все стороны. В любой точке векторы напряженности электрического и магнитного полей взаимно перпендикулярны и перпендикулярны направлению распространения

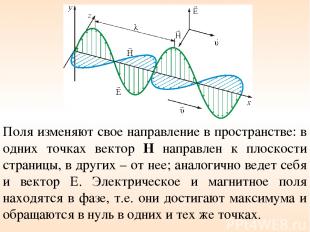
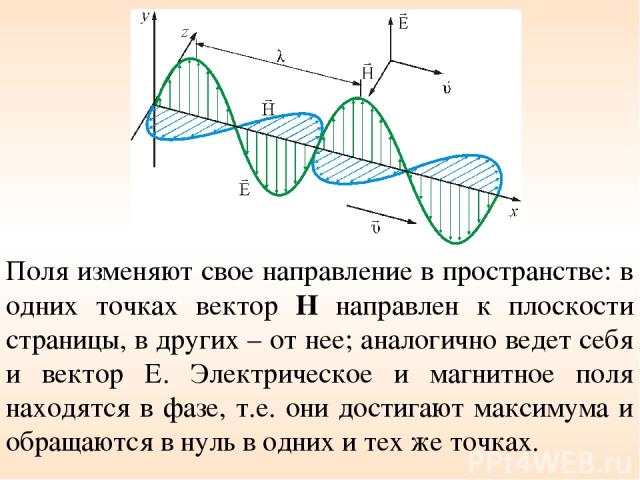
Поля изменяют свое направление в пространстве: в одних точках вектор Н направлен к плоскости страницы, в других – от нее; аналогично ведет себя и вектор Е. Электрическое и магнитное поля находятся в фазе, т.е. они достигают максимума и обращаются в нуль в одних и тех же точках.

Электромагнитные волны представляют собой поперечные волны и, в этом, аналогичны другим типам волн. Однако в ЭМВ происходят колебания полей, а не вещества, как в случае распространения волн на воде или в натянутом шнуре.

4.2 Дифференциальное уравнение ЭМВ Векторы напряженности и поля удовлетворяют волновым уравнениям типа электромагнитного где – оператор Лапласа, υ – фазовая скорость.

Фазовая скорость ЭМВ определяется выражением где – скорость света в вакууме; В веществе скорость распространения электромагнитных возмущений меньше в раз.

Скорость распространения электромагнитных волн в среде зависит от ее электрической и магнитной проницаемостей. Величину абсолютным показателем преломления. С учетом последнего имеем: называют и Следовательно, показатель преломления есть физическая величина, равная отношению скорости электромагнитных волн в вакууме к их скорости в среде.

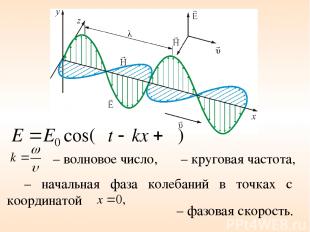
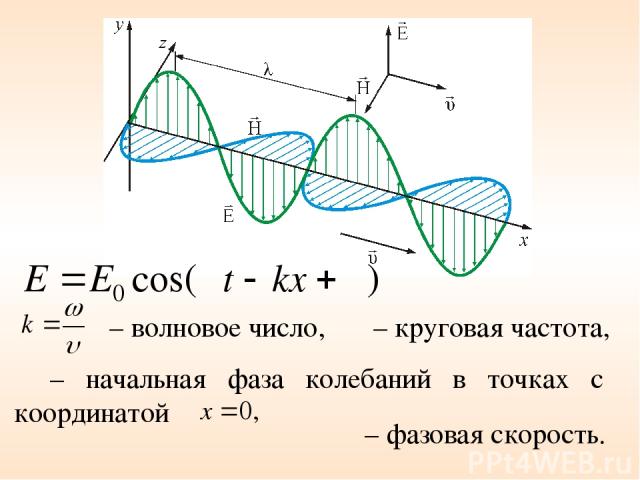
ω – круговая частота, φ – начальная фаза колебаний в точках с координатой – волновое число, υ – фазовая скорость.

Таким образом: • векторы взаимно перпендикулярны, т. к. и направлены одинаково; • электромагнитная волна является поперечной; • электрическая и магнитная составляющие распространяются в одном направлении; колеблются в одинаковых фазах. • векторы

4.3 Энергия и импульс ЭМП Распространение электромагнитных волн связано с переносом ЭМ энергии (подобно тому, как распространение упругих волн в веществе связано с переносом механической энергии). Сама возможность обнаружения ЭМВ указывает на то, что они переносят энергию. ЭМВ - способ передачи энергии и информации (в вакууме)

Для характеристики переносимой волной энергии русским ученым Н.А. Умовым были введены понятия о скорости и направлении движения энергии, о потоке энергии. Спустя десять лет после этого, в 1884 г. английский ученый Джон Пойнтинг описал процесс переноса ЭМ энергии с помощью вектора плотности потока энергии.

Поток энергии через единичную площадку, перпендикулярную направлению распространения волны в единицу времени: Объемная плотность энергии w электромагнитной волны Вектор плотности потока электромагнитной энергии называется вектором Умова-Пойнтинга:

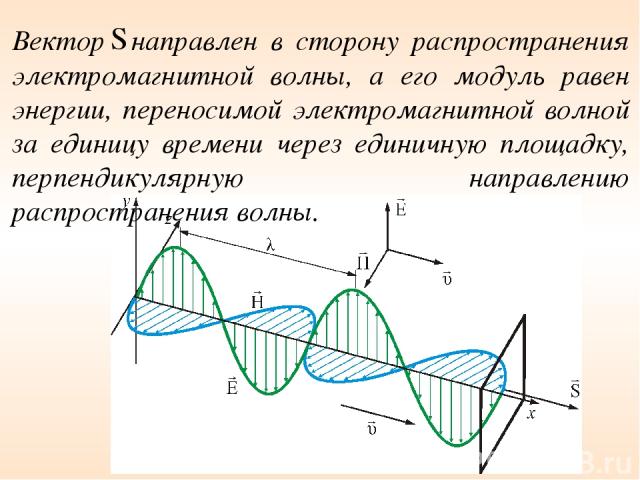
Вектор направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.

“Электромагнитная” масса и импульс Существование давления ЭМВ приводит к выводу о том, что электромагнитному полю (световым квантам) присущ электромагнитный импульс и масса. Модуль среднего значения вектора Умова-Пойнтинга называется интенсивностью:

Опыты Герца были продолжены П. Н. Лебедевым, который в 1894 г. получил ЭМВ длиной 4 – 6 мм и исследовал прохождение их в кристаллах. При этом было обнаружено двойное преломление волн. Дальнейшее развитие методики эксперимента продолжено в 1923 г. А.А. Глаголева-Аркадьева сконструировала массовый излучатель, в котором короткие ЭМВ, возбужденные колебаниями электрических зарядов в атомах и молекулах, генерировались с помощью искр, между металлическими опилками, взвешенными в масле. Так были получены волны длиной λ от 50 мм до 80 мкм. 4.4 Дальнейшее экспериментальное исследование ЭМВ

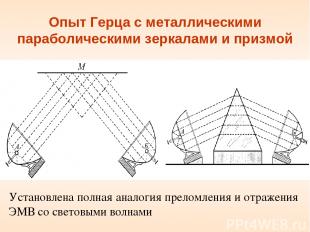
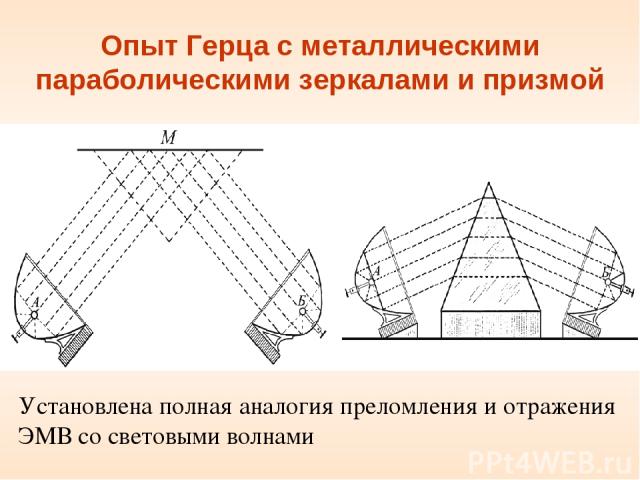
Опыт Герца с металлическими параболическими зеркалами и призмой Установлена полная аналогия преломления и отражения ЭМВ со световыми волнами

Усовершенствовав вибратор Герца и применив свой приемник, профессор Петербургского электротехнического института А.С. Попов 1896 г. наладил опытную радиотелеграфную связь и осуществил с помощью электромагнитных волн передачу сообщения на расстояние около 250 м. В 1899 г. Попов довел расстояние беспроволочной передачи сигналов до 50 км. В 1901 г. была осуществлена радиотелеграфная связь через Атлантический океан. Изобретение электронных ламп (1904 1907) и применение их для генерирования незатухающих колебаний (1913 г.) сделали возможным развитие радиотелеграфии и радиовещания. В 20 30-ых гг. весь мир покрылся сетью мощных радиопередающих станций. Человечество вступило в новую эру коммуникационных отношений.

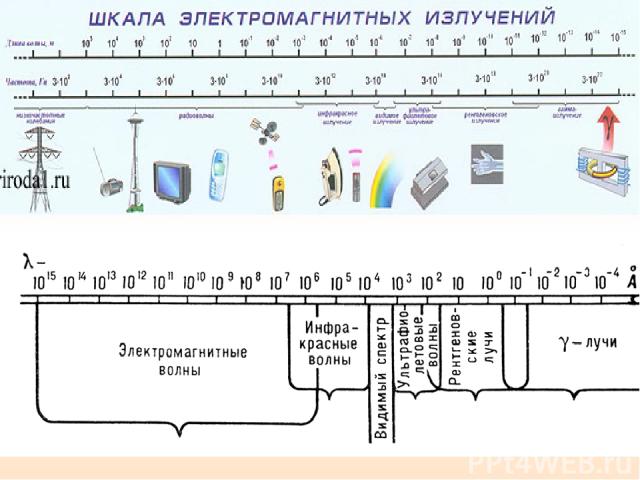
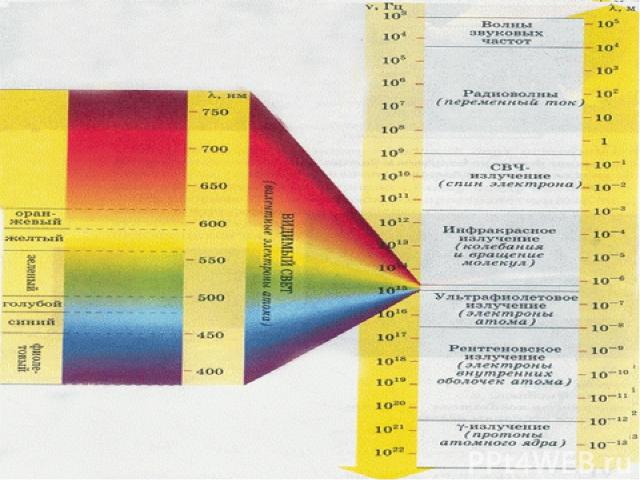
4.5. Шкала ЭМВ В оптике условно рассматривается три области: Длина волны (λ) < размеров приборов; геометрическая оптика. λ сравнима с размеров приборов; волновая оптика. Λ < размеров приборов; квантовая оптика.

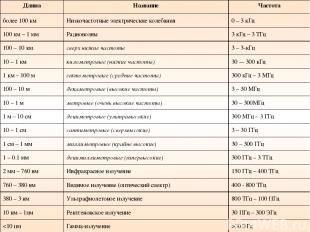
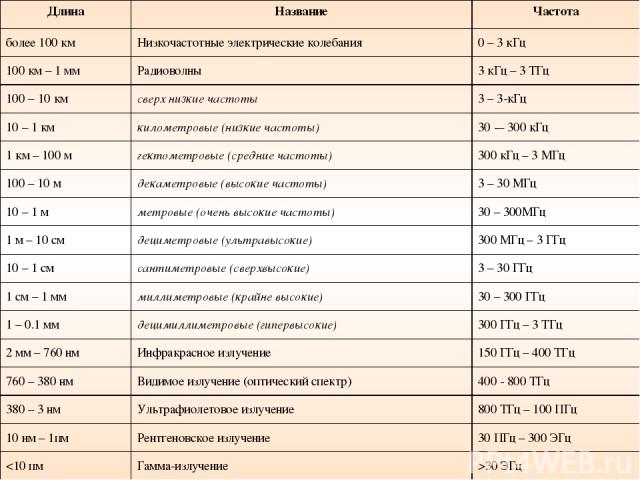
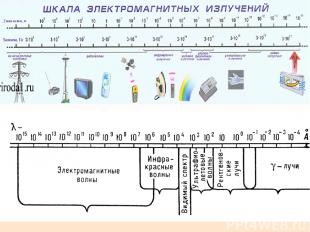
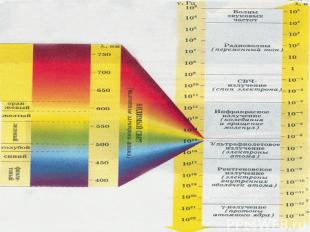
Длина Название Частота более 100 км Низкочастотные электрические колебания 0 – 3 кГц 100 км – 1 мм Радиоволны 3 кГц – 3 ТГц 100 – 10 км сверх низкие частоты 3 – 3-кГц 10 – 1 км километровые (низкие частоты) 30 -– 300 кГц 1 км – 100 м гектометровые (средние частоты) 300 кГц – 3 МГц 100 – 10 м декаметровые (высокие частоты) 3 – 30 МГц 10 – 1 м метровые (очень высокие частоты) 30 – 300МГц 1 м – 10 см дециметровые (ультравысокие) 300 МГц – 3 ГГц 10 – 1 см сантиметровые (сверхвысокие) 3 – 30 ГГц 1 см – 1 мм миллиметровые (крайне высокие) 30 – 300 ГГц 1 – 0.1 мм децимиллиметровые (гипервысокие) 300 ГГц – 3 ТГц 2 мм – 760 нм Инфракрасное излучение 150 ГГц – 400 ТГц 760 – 380 нм Видимое излучение (оптический спектр) 400 - 800 ТГц 380 – 3 нм Ультрафиолетовое излучение 800 ТГц – 100 ПГц 10 нм – 1пм Рентгеновское излучение 30 ПГц – 300 ЭГц 30 ЭГц

КОРПУСКУЛЯРНО-ВОЛНОВАЯ ТЕОРИЯ СВЕТА. ИНТЕРФЕРЕНЦИЯ СВЕТА 3.5 Развитие взглядов на природу света 3.6 Интерференция световых волн 3.7 Опыт Юнга 3.8 Когерентность и монохроматичность 3.9 Методы наблюдения интерференции 3.10 Интерференция в тонких пленках 3.11 Применение интерференции света

3.5 Развитие взглядов на природу света Основные законы геометрической оптики известны ещё с древних времен. Так, Платон (430 г. до н.э.) установил закон прямолинейного распространения света. В трактатах Евклида формулируется закон прямолинейного распространения света и закон равенства углов падения и отражения. Аристотель и Птолемей изучали преломление света. Но точных формулировок этих законов геометрической оптики греческим философам найти не удалось. В конце XVII века, на основе многовекового опыта и развития представлений о свете возникли две мощные теории света – корпускулярная (Ньютон-Декарт) и волновая (Гук-Гюйгенс).

Геометрическая оптика является предельным случаем волновой оптики, когда длина световой волны стремится к нулю. Простейшие оптические явления, например возникновение теней и получение изображений в оптических приборах, могут быть поняты в рамках геометрической оптики. В основу формального построения последней положено четыре закона, установленных опытным путем: • закон прямолинейного распространения света; • закон независимости световых лучей; • закон отражения; • закон преломления света.

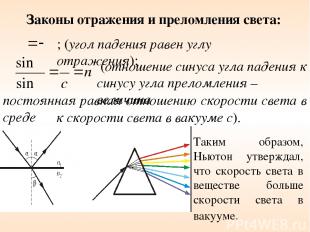
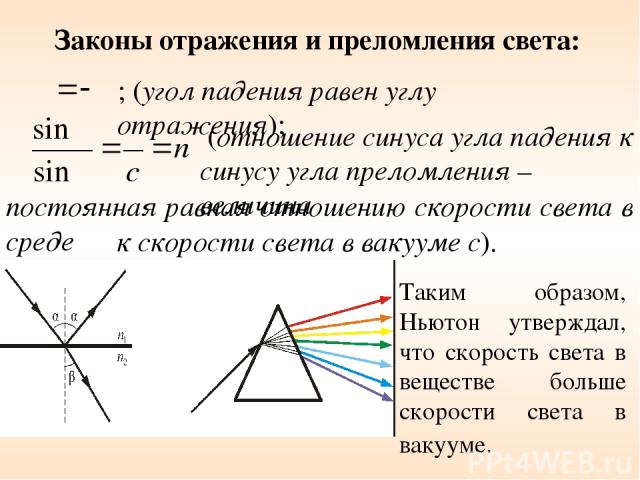
постоянная равная отношению скорости света в среде Законы отражения и преломления света: ; (угол падения равен углу отражения); (отношение синуса угла падения к синусу угла преломления – величина к скорости света в вакууме с). Таким образом, Ньютон утверждал, что скорость света в веществе больше скорости света в вакууме.

Опубликовал в 1690 г. созданную им волновую теорию света, объяснил двойное лучепреломление. Усовершенствовал телескоп; сконструировал окуляр, названный его именем. Открыл кольцо у Сатурна и его спутник Титан. Автор одного из первых трудов по теории вероятностей. Гюйгенс Христиан (1629 – 1695), нидерландский ученый. Жил и работал в Париже. Изобрел маятниковые часы, установил законы колебаний физического маятника. Принцип Гюйгенса

Принцип Гюйгенса Каждая точка, до которой доходит световое возбуждение, является в свою очередь центром вторичных волн; поверхность, огибающая в некоторый момент времени эти вторичные волны, указывает положение к этому моменту фронта действительно распространяющейся волны.

Ферма Пьер (1601 – 1665) – французский математик и физик. Его исследования относятся в большинстве к оптике, где он установил основной принцип геометрической оптики (принцип Ферма). Аналогия между принципом Ферма и вариационными принципами механики сыграла значительную роль в развитии современной динамики и теории оптических инструментов. Принцип Ферма

Согласно принципу Ферма, свет распространяется между двумя точками по пути, для прохождения которого необходимо наименьшее время. Принцип Ферма

Начало XIX в. характеризуется интенсивным развитием математической теории колебаний и волн и ее приложением к объяснению ряда оптических явлений. В связи с работами Т. Юнга и О. Френеля, победа временно перешла к волновой оптике: 1801 г. Т. Юнг сформулировал принцип интерференции и объяснил цвета таких пленок; 1818 г. О. Френель получает премию Парижской Академии за объяснение дифракции; 1840 г. О. Френель и Д. Арго исследуют интерференцию поляризованного света и доказывают поперечность световых колебаний; 3.6 Интерференция световых волн

Френель Огюст Жан (1788 -1827) - французский физик, член Парижской академии наук. Научные работы посвящены физической оптике. Дополнил известный принцип Гюйгенса, введя так называемые зоны Френеля (принцип Гюйгенса - Френеля). Разработал в 1818 году теорию дифракции света. Член Лондонского королевского общества.

Фраунгофер Йозеф (1787-1826) - немецкий физик, профессор Мюнхенского университета. Научные работы относятся к физической оптике. Внёс существенный вклад в исследование дисперсии и создание ахроматических линз. Фраунгофер изучал дифракцию в параллельных лучах (так называемая дифракция Фраунгофера) сначала от одной щели, а потом от многих. Большой заслугой учёного является использование дифракционных решеток для исследования спектров (некоторые ученые считают его изобретателем первой дифракционной решетки).

Волновые свойства света наиболее отчетливо обнаруживают себя в интерференции и дифракции. Пусть две волны одинаковой частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления.

Амплитуда результирующего колебания при сложении колебаний направленных вдоль одной прямой Если разность фаз колебаний возбужденных волнами в некоторой точке пространства остается постоянной во времени, то такие волны называются когерентными.

В случае некогерентных волн разность фаз непрерывно изменяется. Для некогерентных источников интенсивность результирующей волны всюду одинакова и, равна сумме интенсивностей, создаваемых каждой из волн в отдельности:

В случае когерентных волн (для каждой точки пространства) так, что (7.2.2) Последнее слагаемое в этом выражении называется интерференционным членом. В точках пространства, где , (в максимуме ). , интенсивность

Некогерентность естественных источников света обусловлена тем, что излучение тела слагается из волн, испускаемыми многими атомами. Периодическая последовательность горбов и впадин волны и образующиеся в процессе акта излучения одного атома, называется цугом волн или волновым цугом. Фазы каждого цуга волны никак не связаны друг с другом. Атомы излучают хаотически. Процесс излучения одного атома длится примерно с. При этом, длина цуга В одном цуге укладывается примерно длин волн.

Условие максимума и минимума интерференции а вторая разности фаз двух когерентных волн Оптическая разность хода двух волн: L – оптическая длина пути.

Если разность хода равна целому числу длин волн в вакууме условие интерференционного максимума. Если оптическая разность хода то это - условие интерференционного минимума.

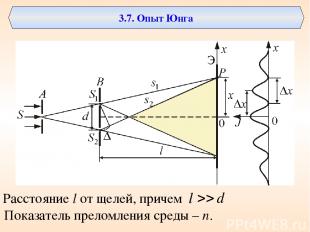
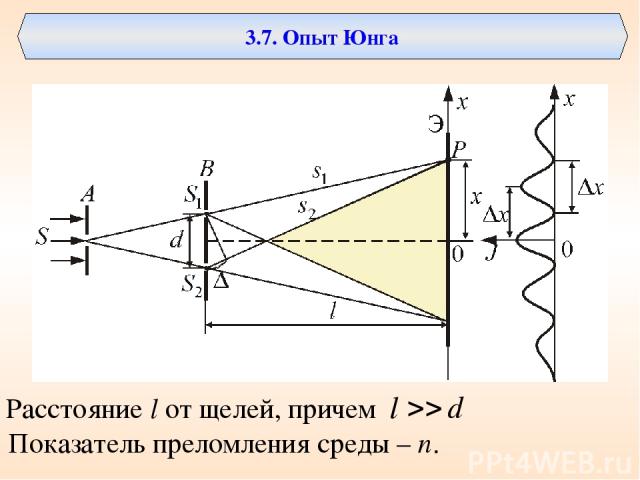
3.7. Опыт Юнга Расстояние l от щелей, причем Показатель преломления среды – n.

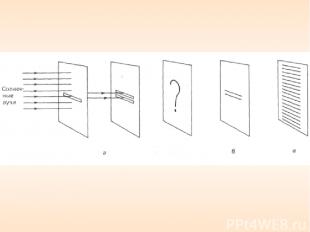
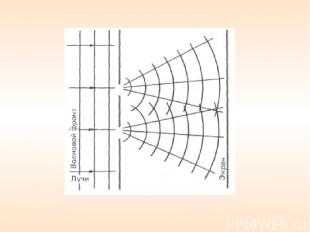
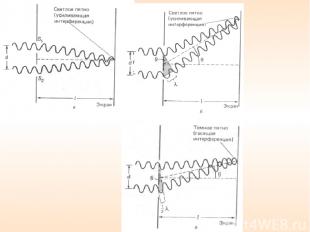
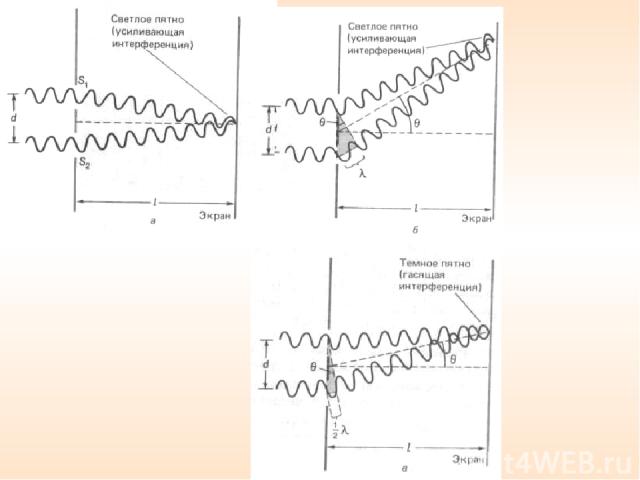
В этом случае происходит ослабляющая (гасящая) интерференция и экран оказывается темным. Так образуется серия светлых и темных полос (или линий). Определим теперь точное положение светлых линий. Прежде всего заметим, что на рис. а масштаб несколько нарушен. В действительности расстояние d между щелями очень мало по сравнению с расстоянием l до экрана. Поэтому лучи от каждой щели, по существу, параллельны, и θ - угол, образуемый ими с горизонталью. Из затемненного треугольника на рис. б видно, что дополнительное расстояние, проходимое нижним лучом, равно dsinθ.

Расстояние между двумя соседними максимумами (или минимумами) равно максимумы интенсивности будут наблюдаться в случае, если (m = 0, 1, 2, …), а минимумы – в случае, если ширина интерференционной полосы.

Главный максимум, соответствующий проходит через точку О. Вверх и вниз от него располагаются максимумы (минимумы) первого , ( ), второго ( ) порядков, и т. д.

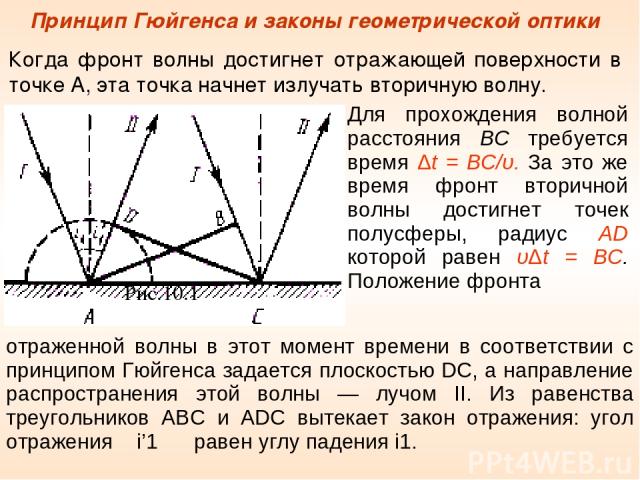
Принцип Гюйгенса и законы геометрической оптики Когда фронт волны достигнет отражающей поверхности в точке А, эта точка начнет излучать вторичную волну. Рис.10.1 Для прохождения волной расстояния ВС требуется время Δt = BC/υ. За это же время фронт вторичной волны достигнет точек полусферы, радиус AD которой равен υΔt = ВС. Положение фронта отраженной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление распространения этой волны — лучом II. Из равенства треугольников ABC и ADC вытекает закон отражения: угол отражения i’1 равен углу падения i1.

Тогда ВС = с t. За это же время фронт волны, возбуждаемой точкой А в среде со скоростью , достигнет точек полусферы, радиус которой AD = t. Положение фронта преломленной волны в этот момент времени в соответствии с принципом Гюйгенса задается плоскостью DC, а направление ее распространения - лучом III. Из рисунка следует, что Для вывода закона преломления предположим, что плоская волна (фронт волны — плоскость АВ), распространяющаяся в вакууме вдоль направления I со скоростью света с, падает на границу раздела со средой, в которой скорость ее распространения равна . Пусть время, затрачиваемое волной для прохождения пути ВС, равно t.

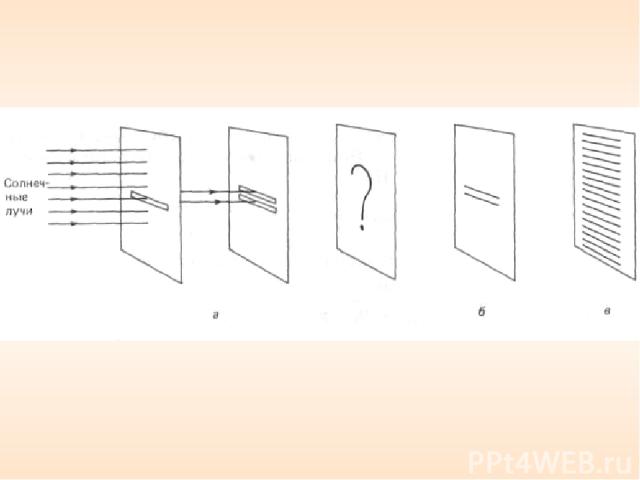
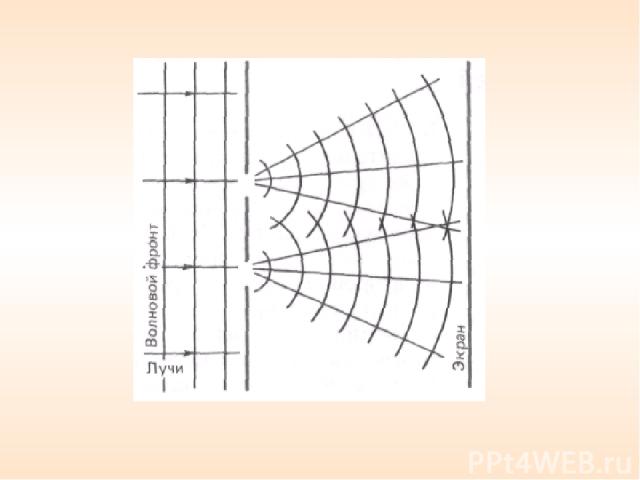
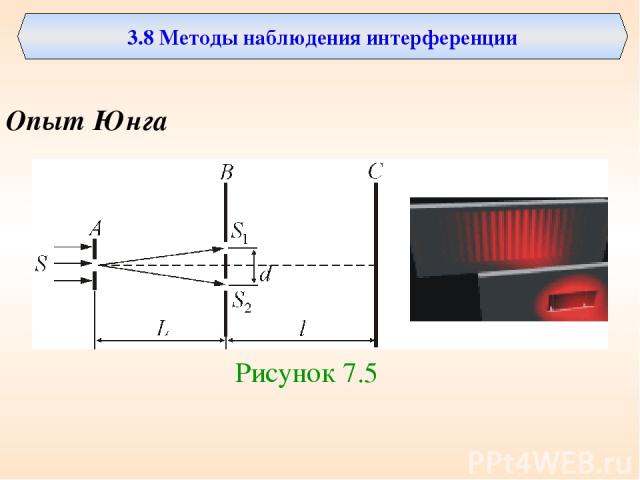
3.8 Методы наблюдения интерференции Опыт Юнга Рисунок 7.5

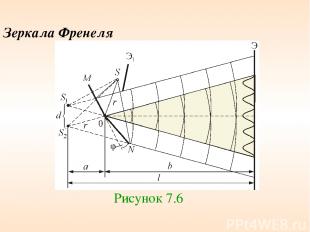
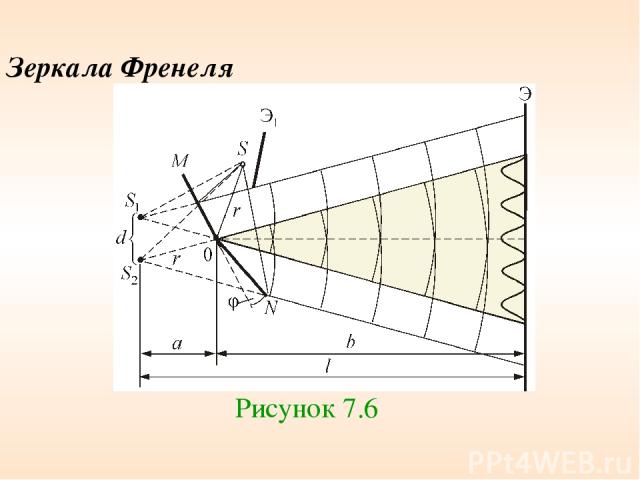
Зеркала Френеля Рисунок 7.6

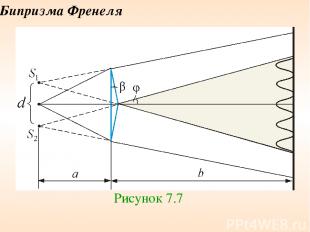
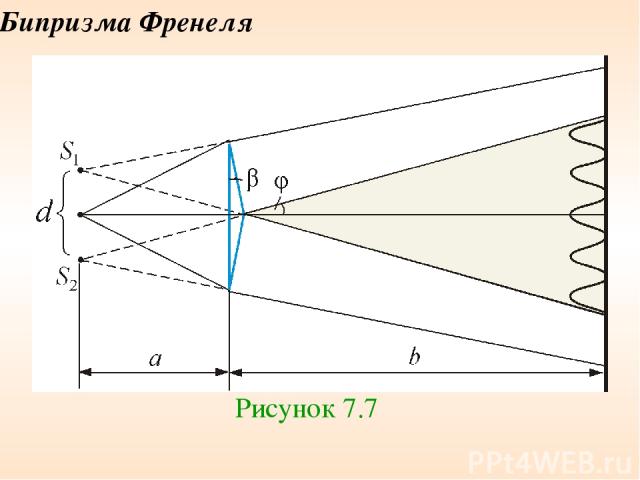
Бипризма Френеля Рисунок 7.7

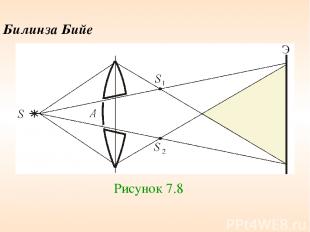
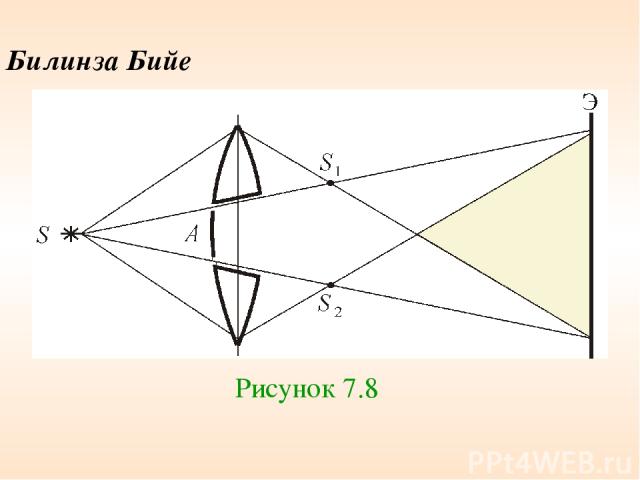
Билинза Бийе Рисунок 7.8

а - световые лучи, отражаясь от верхней и нижней поверхностей тонкого воздушного клина, интерферируют и образуют светлые и темные полосы: б - интерференционная картина, наблюдаемая в случае оптически плоских стеклянных пластин; в - интерференционная картина, наблюдаемая в случае неплоских пластин. 3.9 Интерференция в тонких пленках

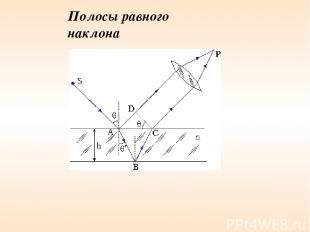
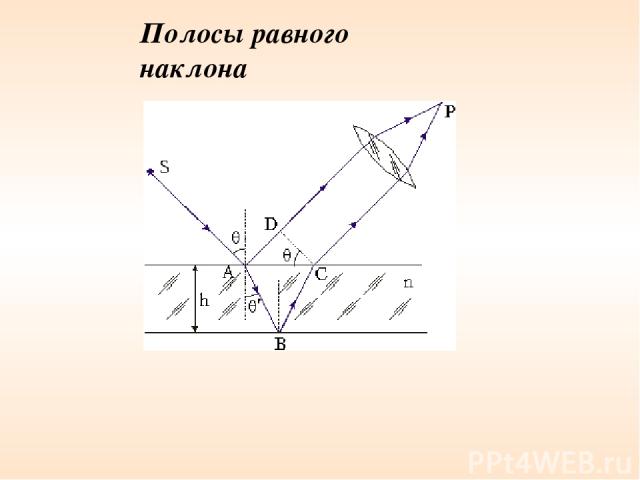
Полосы равного наклона

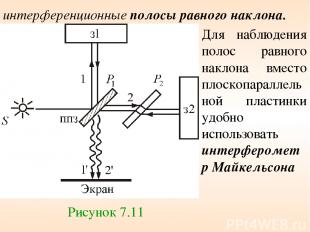
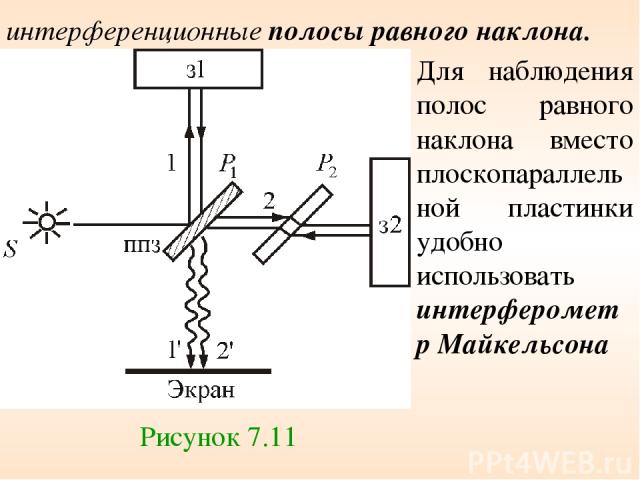
Для наблюдения полос равного наклона вместо плоскопараллельной пластинки удобно использовать интерферометр Майкельсона Рисунок 7.11 интерференционные полосы равного наклона.

Интерференция от клина. Полосы равной толщины В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цвета тонких пленок. Его легко наблюдать на мыльных пузырях, на тонких пленках масла или бензина, плавающих на поверхности воды, на пленках окислов, возникающих на поверхности металлов при закалке, и т.п.

Полосы равной толщины

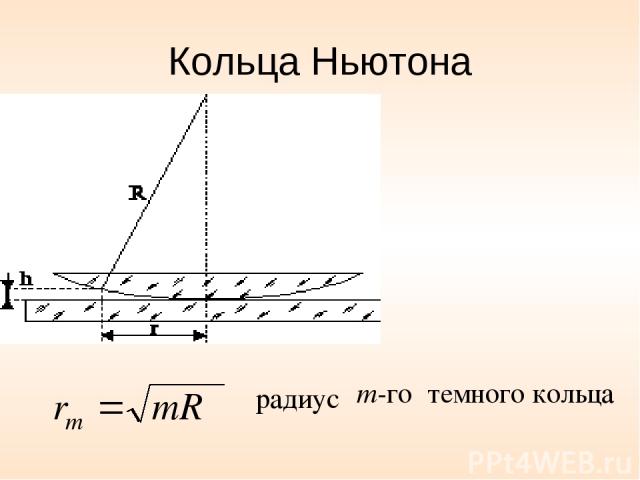
Кольца Ньютона Ньютон объяснил это явление на основе корпускулярной теории света. Кольцевые полосы равной толщины, наблюдаемые в воздушном зазоре между соприкасающимися выпуклой сферической поверхностью линзы малой кривизны и плоской поверхностью стекла, называют кольцами Ньютона.

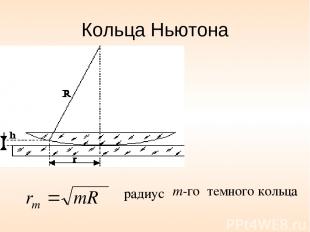
Кольца Ньютона темного кольца m-го радиус

Итак: полосы равного наклона получаются при освещении пластинки постоянной толщины ( ) рассеянным светом в котором содержаться лучи разных направлений. Полосы равной толщины наблюдаются при освещении пластинки переменной толщины (клина) ( ) параллельным пучком света.

3.10 Применение интерференции света • Тот факт, что расположение интерференционных полос зависит от длины волны и разности хода лучей, позволяет по виду интерференционной картины (или их смещению) проводить точные измерения расстояний при известной длине волны или, наоборот, определять спектр интерферирующих волн (интерференционная спектроскопия).

• Кроме того, по интерференционной картине можно выявлять и измерять неоднородности среды (в т.ч. фазовые), в которой распространяются волны, или отклонения формы поверхности от заданной. • Явление интерференционных волн, рассеянных от некоторого объекта (или прошедших через него), с «опорной» волной лежит в основе голографии (в т.ч. оптической, акустической или СВЧ-голографии).

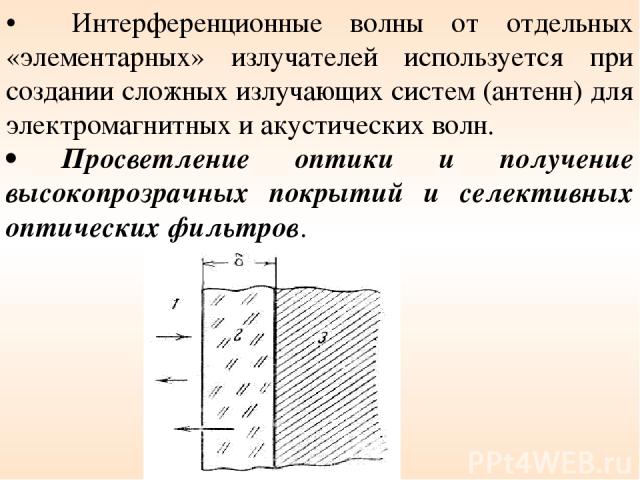
• Интерференционные волны от отдельных «элементарных» излучателей используется при создании сложных излучающих систем (антенн) для электромагнитных и акустических волн. • Просветление оптики и получение высокопрозрачных покрытий и селективных оптических фильтров.

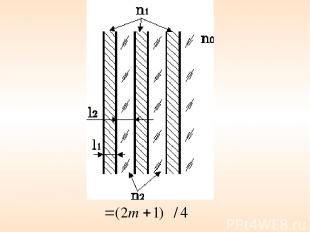
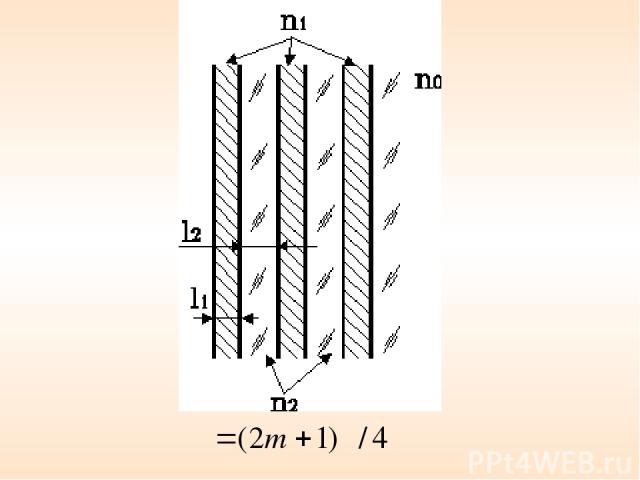
• Получение высокоотражающих электрических зеркал Для получения коэффициента отражения (такие зеркала используются в лазерных резонаторах) надо нанести 11 – 13 слоев.

КОНЕЦ ЛЕКЦИИ