Презентация на тему: Движение молекул

Сегодня * 900igr.net

МОЛЕКУЛЯРНАЯ ФИЗИКА ТЕРМОДИНАМИКА Т П У Доцент кафедры Общей физики Кузнецов Сергей Иванович Сегодня *

Тема 3. ЭЛЕМЕНТЫ ФИЗИЧЕСКОЙ КИНЕТИКИ 3.1. Явления переноса в газах 3.2. Число столкновений и средняя длина свободного пробега молекул в газах 3.3. Диффузия газов 3.4. Внутреннее трение. Вязкость газов 3.5. Теплопроводность газов 3.6. Коэффициенты переноса и их зависимость от давления 3.7. Понятие о вакууме

3.1. Явления переноса в газах Из прошлых лекций мы знаем, что молекулы в газе движутся со скоростью звука, с такой же скоростью движется пуля. Однако, находясь в противоположном конце комнаты, запах разлитой пахучей жидкости мы почувствуем через сравнительно большой промежуток времени. Это происходит потому, что молекулы движутся хаотически, сталкиваются друг с другом, траектория движения у них ломанная.

Рассмотрим некоторые явления, происходящие в газах. Распространение молекул примеси в газе от источника называется диффузией. В состоянии равновесия температура Т и концентрация n во всех точках системы одинакова. При отклонении плотности от равновесного значения в некоторой части системы возникает движение компонент вещества в направлениях, приводящих к выравниванию концентрации по всему объему системы.

Связанный с этим движением перенос вещества обусловлен диффузией. Диффузионный поток будет пропорционален градиенту концентрации:

Если какое либо тело движется в газе, то оно сталкивается с молекулами газа и сообщает им импульс. С другой стороны, тело тоже будет испытывать соударения со стороны молекул, и получать собственный импульс, но направленный в противополож-ную сторону. Газ ускоряется, тело тормозиться, то есть, на тело действуют силы трения. Такая же сила трения будет действовать и между двумя соседними слоями газа, движущимися с разными скоростями.

Это явление носит название внутреннее трение или вязкость газа, причём сила трения пропорциональна градиенту скорости: (3.1.1)

Если в соседних слоях газа создана и поддерживается разность температур, то между ними будет происходить обмен тепла. Благодаря хаотическому движению, молекулы в соседних слоях будут перемешиваться и, их средние энергии будут выравниваться. Происходит перенос энергии от более нагретых слоев к более холодным.

называется теплопроводностью. Поток тепла пропорционален градиенту температуры: (3.1.2) Перенос энергии от более нагретых слоев к более холодным

В состоянии равновесия в среде, содержащей заряженные частицы, потенциал электрического поля в каждой точке соответствует минимуму энергии системы. При наложении внешнего электрического поля возникает неравновесное движение электрических зарядов в таком направлении, чтобы минимизировать энергию системы в новых условиях.

Связанный с этим движением перенос электрического заряда называется электропроводностью, а само направленное движение зарядов электрическим током.

В процессе диффузии, при тепло и электропроводности происходит перенос вещества, а при внутреннем трении – перенос энергии. В основе этих явлений лежит один и тот же механизм – хаотическое движение молекул. Общность механизма, обуславливающего все эти явления переноса, приводит к тому, что их закономерности должны быть похожи друг на друга.

3.2. Число столкновений и средняя длина свободного пробега молекул в газах Обозначим – длина свободного пробега молекулы. Медленность явлений переноса, например диффузии ароматических веществ – «распространение запаха», при относительно высокой скорости теплового движения молекул ( ) объясняется столкновениями молекул.

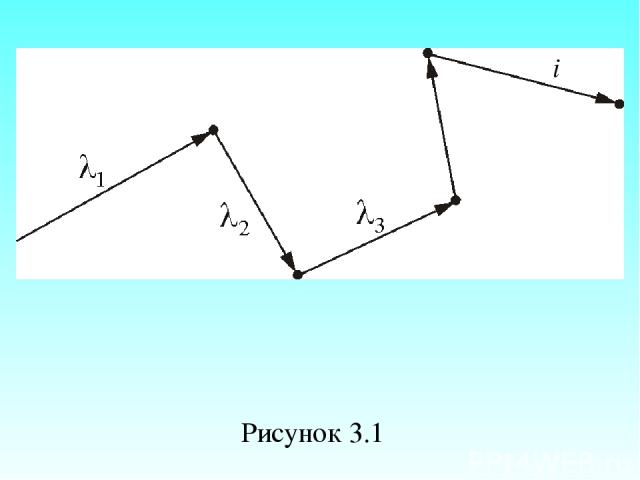
Расстояние, проходимое молекулой в среднем без столкновений, называется средней длиной свободного пробега: – средняя скорость теплового движения, – среднее время между двумя столкновениями. Именно средняя длина свободного пробега, нас и интересует (рисунок 3.1).

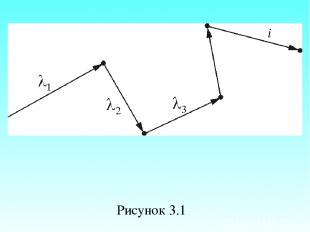
Рисунок 3.1

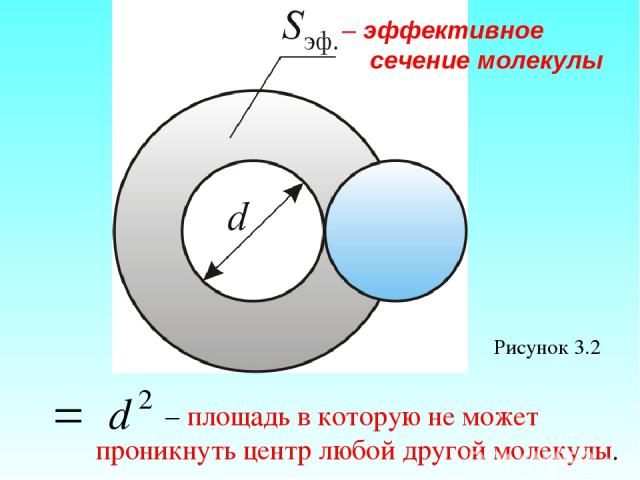
Модель идеального газа – твёрдые шарики одного диаметра, взаимодействую-щие между собой только при столкновении. Обозначим σ – эффективное сечение молекулы – полное поперечное сечение рассеяния, характеризующее столкновение между двумя молекулами (рисунок 3.2).

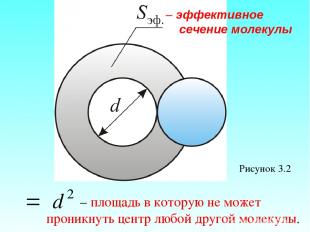
Рисунок 3.2 – эффективное сечение молекулы – площадь в которую не может проникнуть центр любой другой молекулы.

За одну секунду молекула проходит путь, равный средней арифметической скорости За ту же секунду молекула претерпе-вает ν столкновений.

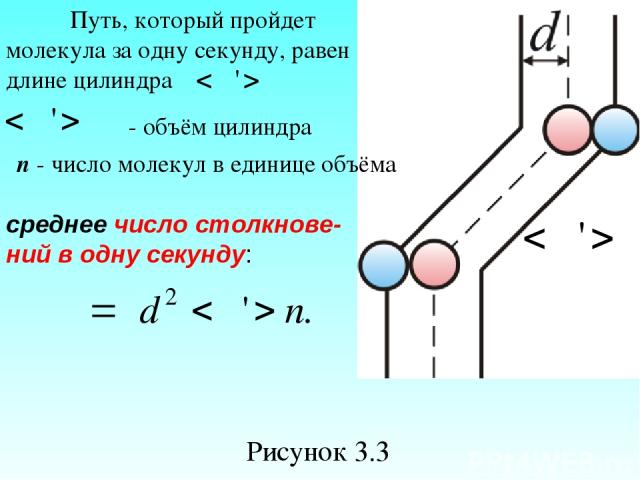
Подсчитаем число столкновений ν. Вероятность столкновения трех и более молекул бесконечно мала. Предположим, что все молекулы застыли, кроме одной. Её траектория будет представлять собой ломаную линию. Столкновения будут только с теми молекулами, центры которых лежат внутри цилиндра радиусом d (рисунок 3.3).

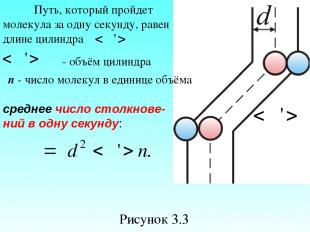
Рисунок 3.3 Путь, который пройдет молекула за одну секунду, равен длине цилиндра - объём цилиндра n - число молекул в единице объёма среднее число столкнове- ний в одну секунду:

На самом деле, все молекулы движутся (и в сторону и навстречу друг другу), поэтому число соударений определяется средней скоростью движения молекул относительно друг друга По закону сложения случайных величин: Так как - средняя длина свободного пробега Тогда:

Из уравнения состояния идеального газа выразим n через давление P и температуру Т Так как , то есть тогда

Таким образом, при заданной температуре, средняя длина свободного пробега обратно пропорциональна давлению Р: Например: d = 3 Å = 3 10 10 м, Р = 1 атм., Т = 300 К, а, т.к столкновений.

3.3. Диффузия газов Диффузия от латинского diffusio – распространение, растекание взаимное проникновение соприкасающихся веществ друг в друга, вследствие теплового движения частиц вещества. Диффузия происходит в направлении уменьшения концентрации вещества и ведет к его равномерному распределению по занимаемому объему.

Диффузия имеет место в газах, жидкостях и твердых телах. Наиболее быстро диффузия происходит в газах, медленнее в жидкостях, еще медленнее в твердых телах, что обусловлено характером движения частиц в этих средах. Для газа диффузия – это распределение молекул примеси от источника (или взаимная диффузия газа).

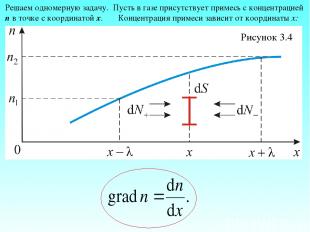
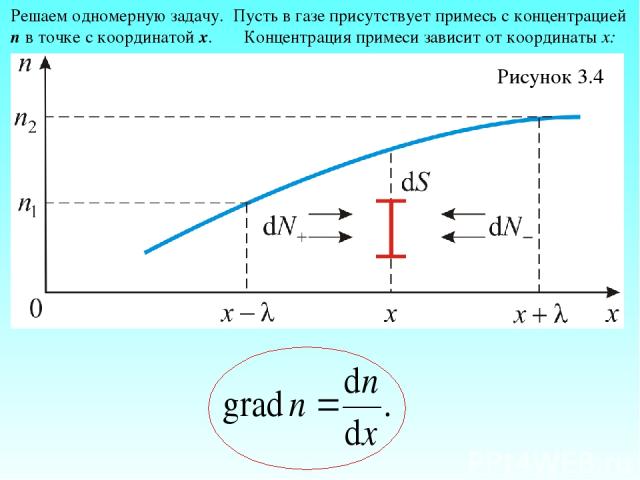
Рисунок 3.4 Решаем одномерную задачу. Пусть в газе присутствует примесь с концентрацией n в точке с координатой х. Концентрация примеси зависит от координаты х:

Градиент концентрации, в общем случае равен . (3.3.1) Так как у нас одномерная задача, то При наличии grad n, хаотическое движение будет более направленным и возникнет поток молекул примеси, направленный от мест с большей концентрацией к местам с меньшей концентрацией. Найдём этот поток.

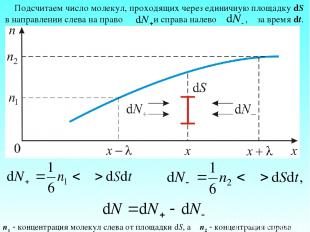
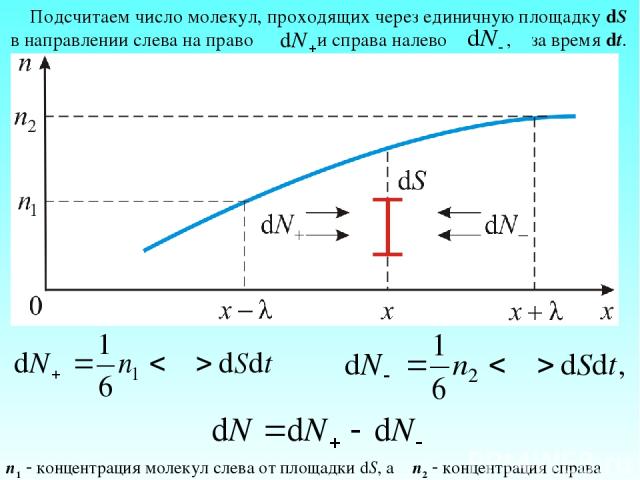
Подсчитаем число молекул, проходящих через единичную площадку dS в направлении слева на право и справа налево , за время dt. n1 концентрация молекул слева от площадки dS, а n2 концентрация справа

Результирующий диффузионный поток через единицу площади в единицу времени: но тогда

Обозначим: – коэффициент диффузии. Тогда диффузионный поток будет равен: (3.3.2) или в общем случае (в трёхмерной системе) (3.3.3) – уравнение Фика.

Из уравнения Фика видно, что диффузионный поток, направлен в сторону уменьшения концентрации. При этом коэффициент диффузии D численно равен диффузионному потоку через единицу площади в единицу времени при Измеряется коэффициент диффузии D в м/с2.

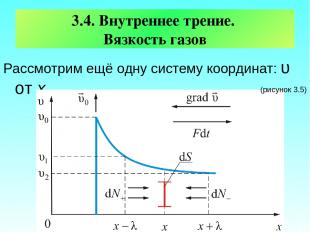
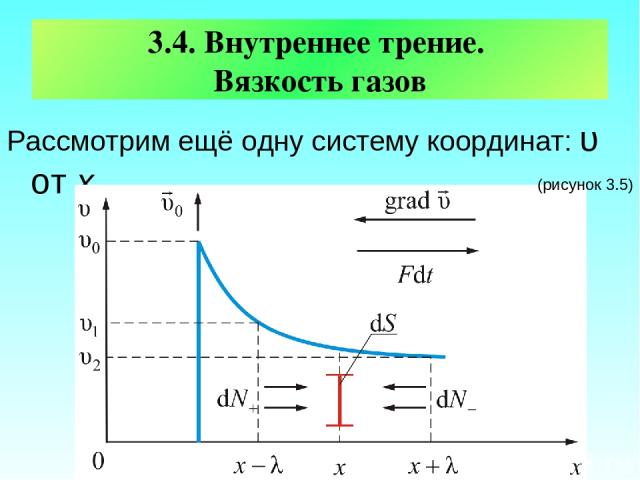
3.4. Внутреннее трение. Вязкость газов Рассмотрим ещё одну систему координат: υ от х (рисунок 3.5)

Пусть в покоящемся газе вверх, перпендикулярно оси х движется пластинка со скоростью υ0, причём (υT – скорость теплового движения молекул). Пластинка увлекает за собой прилегающий слой газа, тот слой – соседний и так далее. Весь газ делится, как бы на тончайшие слои, скользящие вверх тем медленнее, чем дальше они от пластинки. Раз слои газа движутся с разными скоростями, возникает трение. Выясним причину трения в газе.

Каждая молекула газа в слое принимает участие в двух движениях: тепловом и направленном. Так как направление теплового движения хаотически меняется, то в среднем вектор тепловой скорости равен нулю . При направленном движении вся совокупность молекул будет дрейфовать с постоянной скоростью υ.

Средний импульс отдельной молекулы в слое определяется только дрейфовой скоростью υ: Но так как молекулы участвуют в тепловом движении, они будут переходить из слоя в слой. При этом они будут переносить с собой добавочный импульс, который будет определяться молекулами того слоя, куда перешла молекула. Перемешивание молекул разных слоёв приводит к выравниванию дрейфовых скоростей разных слоёв, что и проявляется макроскопически как действие сил трения между слоями.

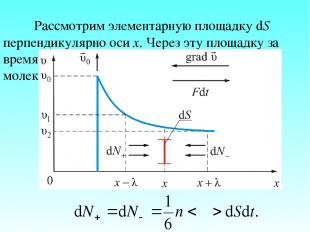
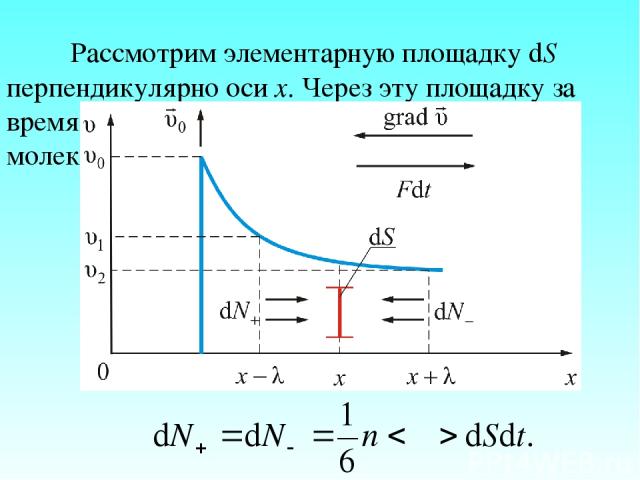
Рассмотрим элементарную площадку dS перпендикулярно оси х. Через эту площадку за время dt влево и вправо переходят потоки молекул.

Но эти потоки переносят разный импульс: и При переносе импульса от слоя к слою происходит изменение импульса этих слоёв. Это значит, что на каждый из этих слоёв действует сила, равная изменению импульса. Сила эта есть не что другое, как сила трения между слоями газа, движущимися с различными скоростями. Отсюда и название – внутреннее трение.

Закон вязкости был открыт И. Ньютоном в 1687 г. Переносимый за время dt импульс равен: Или Отсюда получим силу, действующую на единицу площади поверхности, разделяющей два соседних слоя газа:

Сила, действующая на единицу площади поверхности, разделяющей два соседних слоя газа: Или, в общем виде Это уравнение Ньютона. Здесь η – коэффициент вязкости: (3.4.3) где D – коэффициент диффузии; ρ – плотность газа

Физический смысл коэффициента вязкости η в том, что он численно равен импульсу, переносимому в единицу времени через единицу площади при градиенте скорости равном единице.

3.5. Теплопроводность газов Учение о теплопроводности начало развиваться в XVIII в. и получило свое завершение в работах французского ученого Ж. Фурье (1786 – 1830), опубликовавшего в 1822 г. книгу «Аналитическая теория теплоты».

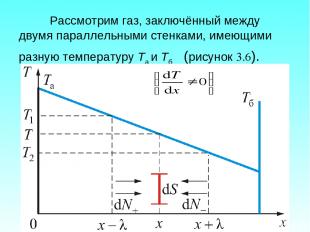
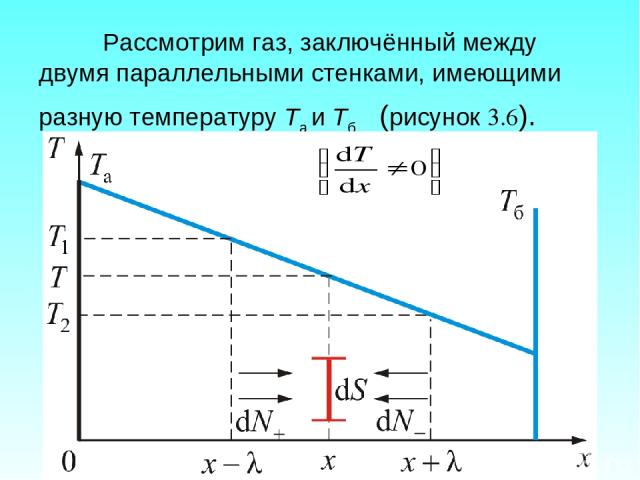
Рассмотрим газ, заключённый между двумя параллельными стенками, имеющими разную температуру Та и Тб (рисунок 3.6).

Итак, у нас имеется градиент температуры Тогда через газ в направлении оси х будет идти поток тепла. Хаотично двигаясь, молекулы будут переходить из одного слоя газа в другой, перенося с собой энергию. Это движение молекул приводит к перемешиванию молекул, имеющих различную кинетическую энергию : здесь i – число степеней свободы молекулы.

При подсчёте потока тепла введём следующие упрощения: Среднеарифметическая скорость теплового движения молекул Концентрация молекул в соседних слоях одинакова, (хотя на самом деле она различается, что даёт ошибку 10 %).

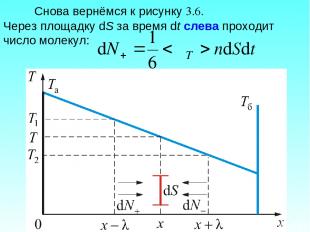
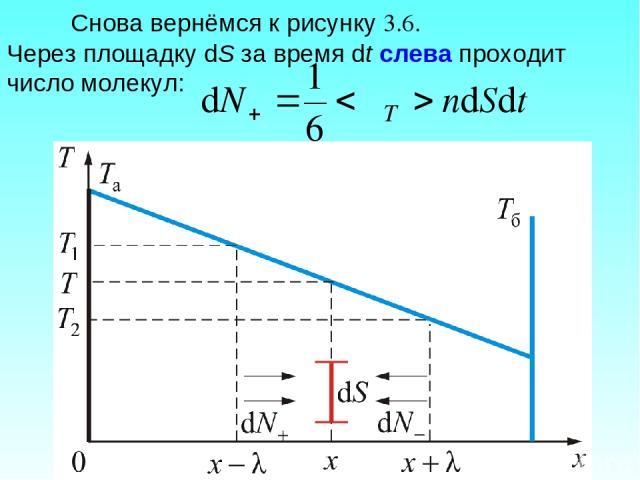
Снова вернёмся к рисунку 3.6. Через площадку dS за время dt слева проходит число молекул:

Средняя энергия этих молекул К – соответствует значению энергии в том месте, где они испытывают последний раз столкновение. Для одной молекулы газа: Соответственно, справа проходит молекул. Каждая из этих молекул перенесёт энергию

Результирующий поток энергии через dS равен разности потоков и , то есть Применяя те же рассуждения, получим: результирующий поток через единичную площадку в единицу времени равен q и направлен он в сторону противоположную направлению градиента: ,

или (3.5.1) – уравнение теплопроводности Ж.Фурье. Здесь q – тепловой поток; χ – коэффициент теплопроводности, равный: или (3.5.2) (3.5.3)

υТ – тепловая скорость молекул; – удельная теплоемкость при постоянном объеме. Найдем размерность коэффициента теплопроводности:

3.6. Уравнения и коэффициенты переноса Сопоставим уравнения переноса Уравнение Фика для диффузии. Коэффициент диффузии

или Уравнение Ньютона для трения. Коэффициент вязкости:

или Уравнение Фурье для теплопроводности. Коэффициент теплопроводности:

Все эти законы были установлены опытно, задолго до обоснования молекулярно-кинетической теорией. Эта теория позволила установить, что внешнее сходство уравнений обусловлено общностью лежащих в их основе молекулярного механизма перемешивания молекул в процессе их теплового хаотического движения.

Однако к концу XIX века, несмотря на блестящие успехи молекулярно-кинетической теории ей недоставало твёрдой опоры – прямых экспериментов, доказывающих существование атомов и молекул. Это дало возможность некоторым, философам, проповедовавшим субъективный идеализм заявлять, что схожесть формул – это произвол учёных, упрощённое математическое описание явлений.

Но это конечно не так. Все выше указанные коэффициенты связаны между собой и все выводы молекулярно – кинетической теории подтверждены опытно.

Зависимость коэффициентов переноса от давления Р Так как скорость теплового движения молекул и не зависит от давления Р, а коэффициент диффузии D ~ λ , то и зависимость D от Р должна быть подобна зависимости λ(Р). При обычных давлениях и в разряженных газах в высоком вакууме D = const.

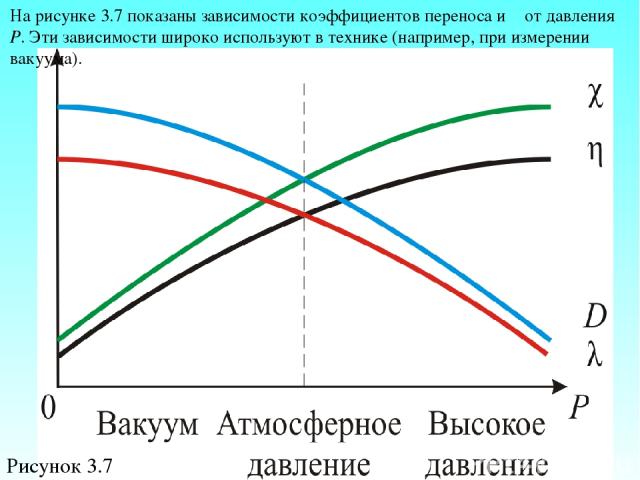
С ростом давления λ уменьшается и затрудняется диффузия ( ). В вакууме и при обычных давлениях отсюда, и С увеличением Р и ρ, повышается число молекул переносящих импульс из слоя в слой, но зато уменьшается расстояние свободного пробега λ. Поэтому, вязкость η и теплопроводность χ, при высоких давлениях, не зависят от Р (η и χ – const). Все эти результаты подтверждены экспериментально (Рис 3.7).

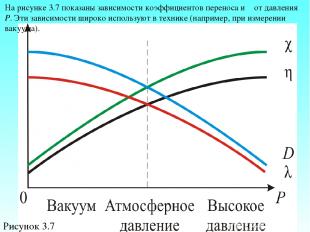
Рисунок 3.7 На рисунке 3.7 показаны зависимости коэффициентов переноса и λ от давления Р. Эти зависимости широко используют в технике (например, при измерении вакуума).

Молекулярное течение. Эффузия газов Молекулярное течение – течение газов в условиях вакуума, то есть когда молекулы не сталкиваются друг с другом. Течение газа в условиях вакуума через отверстие (под действием разности давлений) называется эффузией газа.

В вакууме происходит передача импульса непосредственно стенкам сосуда, то есть, происходит трение газа о стенки сосуда. Трение перестаёт быть внутренним, и понятие вязкости теряет свой прежний смысл (как трение одного слоя газа о другой).

Как при молекулярном течении, как и при эффузии, количество протекающего в единицу времени газа обратно пропорционально корню квадратному из молярной массы: . Эту зависимость тоже широко используют в технике, например – для разделения изотопов газа U235 (отделяют от U238, используя газ UF6).

3.7. Понятие о вакууме Газ называется разреженным, если его плотность столь мала, что средняя длина свободного пробега молекул может быть сравнима с линейными размерами l сосуда, в котором находится газ. Такое состояние газа называется вакуумом. Различают следующие степени вакуума: сверхвысокий ( ), высокий ( ), средний ( ) и низкий вакуум.

Свойства разряженных газов отличаются от свойств неразряженных газов. Это видно из таблицы, где приведены некоторые характеристики различных степеней вакуума.

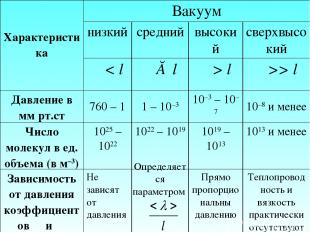
Определяется параметром Характеристика Вакуум низкий средний высокий сверхвысокий λ < l λ ≈ l λ > l λ >> l Давление в мм рт.ст 760 – 1 1 – 10–3 10–3 – 10–7 10–8 и менее Число молекул в ед. объема (в м–3) 1025 – 1022 1022 – 1019 1019 – 1013 1013 и менее Зависимость от давления коэффициентов χ и η Не зависят от давления Прямо пропорциональны давлению Теплопроводность и вязкость практически отсутствуют

Если из сосуда откачивать газ, то по мере понижения давления число столкновений молекул друг с другом уменьшается, что приводит к увеличению их длины свободного пробега. При достаточно большом разрежении столкновения между молекулами относительно редки, поэтому основную роль играют столкновения молекул со стенками сосуда.

В состоянии высокого вакуума уменьшение плотности разряженного газа приводит к соответствующей убыли частиц без изменения . Следовательно, уменьшается число носителей импульса или внутренней энергии в явлениях вязкости и теплопроводности. Коэффициент переноса в этих явлениях прямо пропорциональны плотности газа. В сильно разряженных газах внутреннее трение по существу отсутствует.

Удельный тепловой поток в сильно разряженных газах пропорционален разности температур и плотности газа. Стационарное состояние разряженного газа, находящегося в двух сосудах, соединенных узкой трубкой, возможно при условии равенства встречных потоков частиц, перемещающихся из одного сосуда в другой: , где n1 и n2 – число молекул в 1 см3 в обоих сосудах; и – их средние арифметические скорости.

Если Т1 и Т2 – температуры газа в сосудах, то предыдущее условие стационарности можно переписать в виде уравнения, выражающего эффект Кнудсена: где P1 и P2 – давления разряженного газа в обоих сосудах.

Вопросы создания вакуума имеют большое значение в технике, так как например, во многих современных электронных приборах используются электронные пучки, формирование которых возможно лишь в условиях вакуума. Для получения различных степеней разряжения применяются вакуумные насосы, позволяющие получить предварительное разряжение (форвакуум) до ≈ 0,13 Па, а также вакуумные насосы и лабораторные приспособления, позволяющие получить давление до 13,3 мкПа – 1, 33 пПа (10–7 – 10–14 мм рт.ст.).