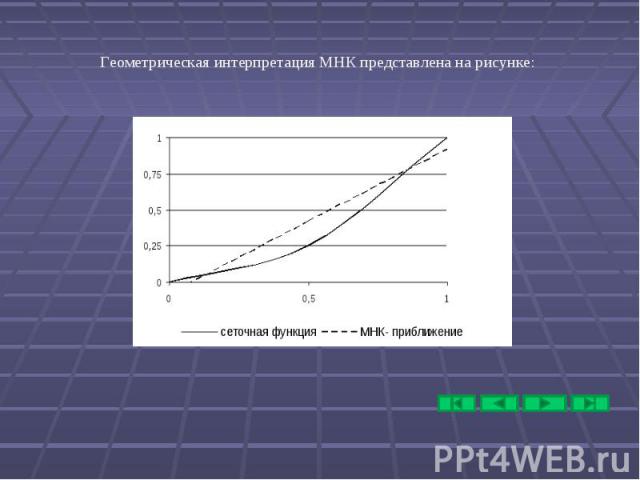
Презентация на тему: МЕТОДЫ ВЫЧИСЛЕНИЙ В ЭКОНОМИКЕ"

Методы вычислений в экономическом моделировании

Методы вычислений в экономическом моделировании Использование математических методов в экономике восходит к работам Ф.Кенэ («Экономическая таблица»), А. Смита (классическая макроэкономическая модель), Д.Риккардо (модель международной торговли). Моделированию рыночной экономики посвящены работы Л.Вальраса, О.Курно, В.Парето. С применением математических методов связаны работы В.В. Леонтьева, Р.Солоу, П.Самуэльсона, Д.Хикса, В.С Немчинова, В.В Новожилова, Л.В. Канторовича и многих других выдающихся ученых. Примерами экономических моделей являются модели фирмы, модели экономического роста, модели потребительского выбора, модели равновесия на финансовых и товарных рынках. Построение экономической модели требует выполнения ряда шагов. Сначала формулируется предмет и цель исследования. Затем экономисты выявляют структурные и функциональные элементы модели, взаимосвязи между ними, существенные факторы, отвечающие цели исследования и отбрасывают то, что несущественно для решения задачи. На заключительном этапе проводятся расчеты по математической модели и анализ полученного решения. Именно на завершающем этапе применяются численные методы. В данном разделе на материале ряда экономических моделей иллюстрируется применение методов численного решения нелинейных уравнений, систем алгебраических уравнений, численного интегрирования и методов решения дифференциальных уравнений.

Статические балансовые модели Системы линейных алгебраических уравнений применяются в макроэкономике для проведения балансового анализа многоотраслевого хозяйства. Цель балансового анализа — ответить на вопрос, каким должен быть объем производства каждой из отраслей хозяйства, чтобы удовлетворить все потребности в продукции этой отрасли? Предполагается, что каждая отрасль выступает одновременно как производитель некоторого вида продукции и как потребитель продукции других (в том числе своей) отраслей. Процесс производства рассматривается за некоторый период времени, например, за год.

Статические балансовые модели

Статические балансовые модели

Статические балансовые модели

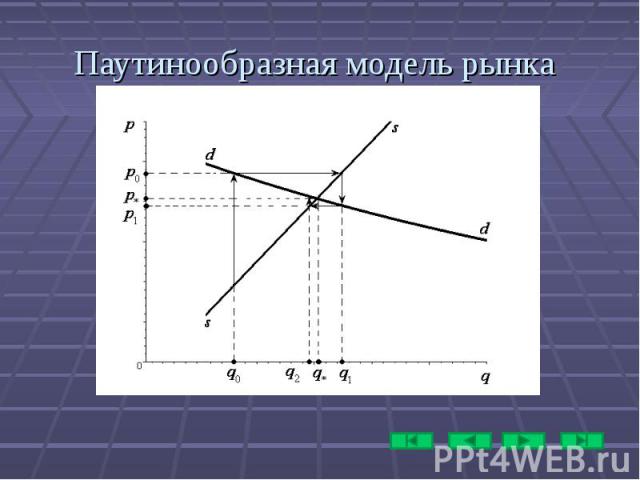
Некоторые модели экономической динамики Паутинообразная модель рынка Дифференциальные уравнения в экономической динамике. Модель экономического роста.

Паутинообразная модель рынка

Паутинообразная модель рынка

Паутинообразная модель рынка

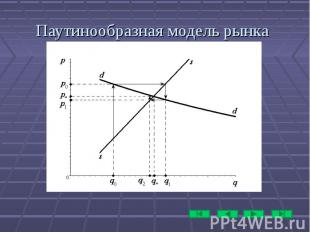
Паутинообразная модель рынка

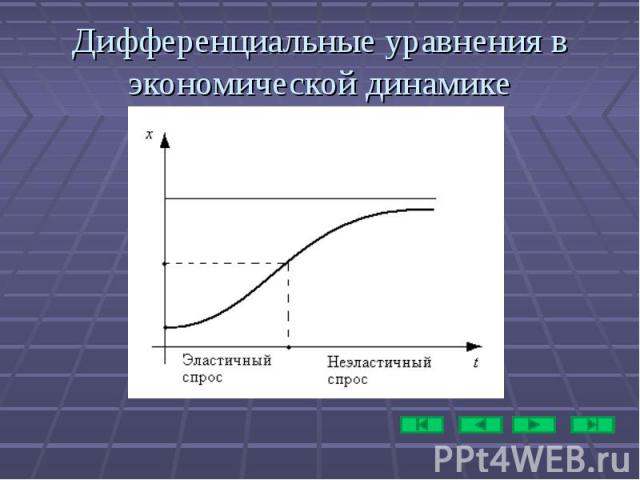
Дифференциальные уравнения в экономической динамике

Дифференциальные уравнения в экономической динамике

Дифференциальные уравнения в экономической динамике

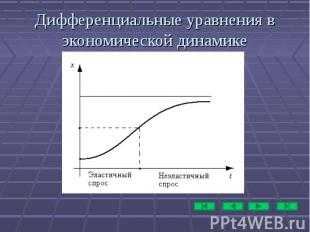
Дифференциальные уравнения в экономической динамике

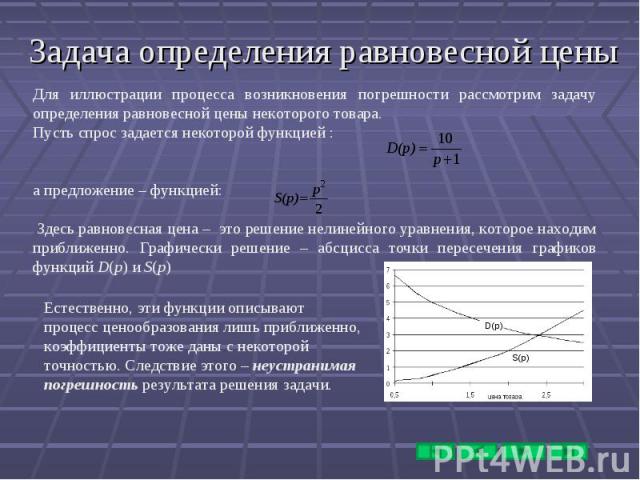
Методы вычислений в финансовых расчетах

Определение уровня процентной ставки. Пусть в течение n лет фирма перечисляет в банк p раз в году средства в размере R/p денежных единиц (R – величина суммарного годового платежа) с целью создания фонда накопления. Банк начисляет проценты на данные взносы m раз в году по сложной процентной ставке j. Определим наращенную сумму (величину фонда накопления) такого потока платежей на момент окончания выплат.

Определение уровня процентной ставки.

Определение уровня процентной ставки.

Вычисление наращенных сумм на основе непрерывных процентных ставок Силой роста называется специальная процентная ставка, характеризующая относительный прирост наращенной суммы. Согласно данному определению на бесконечно малом промежутке имеем

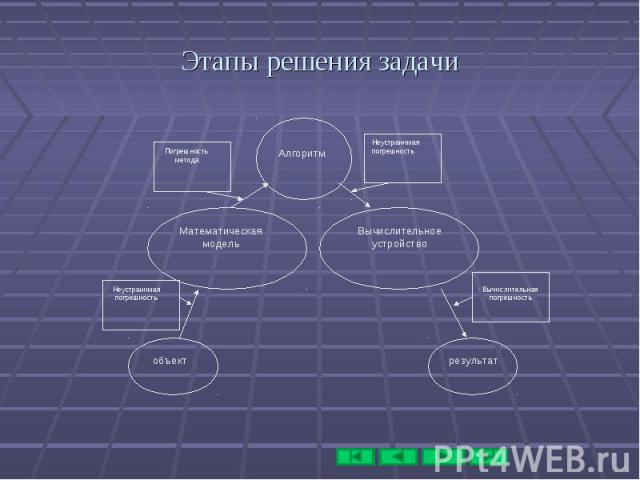
Погрешность результата численного решения задачи. Основные этапы решения задачи с помощью компьютера. Характеристика погрешности Приближенные методы решения нелинейных уравнений Решение задач линейной алгебры Интерполяция Численное интегрирование Численное решение задачи Коши Метод наименьших квадратов Литература

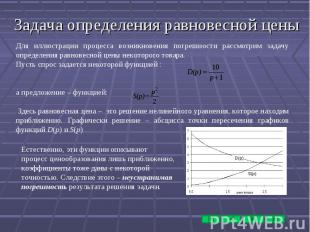
Абсолютная и относительная погрешности. Пусть x* - приближенное  значение x. Абсолютной погрешностью приближения  называется величина А(x*), для которой справедливо неравенство: |x - x*|≤ А(x*) Величина Δ(x*), удовлетворяющая неравенству |x - x*|/ |x*| ≤ Δ(x*) называется относительной погрешностью x*. Абсолютная погрешность зависит от выбора системы единиц измерения x*. Относительная погрешность – величина безразмерная, иногда вычисляется в процентах. Абсолютная и относительная погрешности связаны соотношением: А(x*) = |x*| Δ(x*). Значащими цифрами в записи числа называются все цифры в его записи, начиная с первой ненулевой. Значащая цифра называется верной, если абсолютная погрешность этого числа не превосходит половины единицы разряда, соответствующего этой цифре. Остальные цифры называются сомнительными. Таким образом, в числе x* = a110n + a210n – 1 + … +am10n – m + 1 цифра ak считается верной, если А(x*) ≤ 0,5·10n – k + 1. Количеством верных цифр после запятой называется количество цифр в числе после запятой до первой сомнительной.

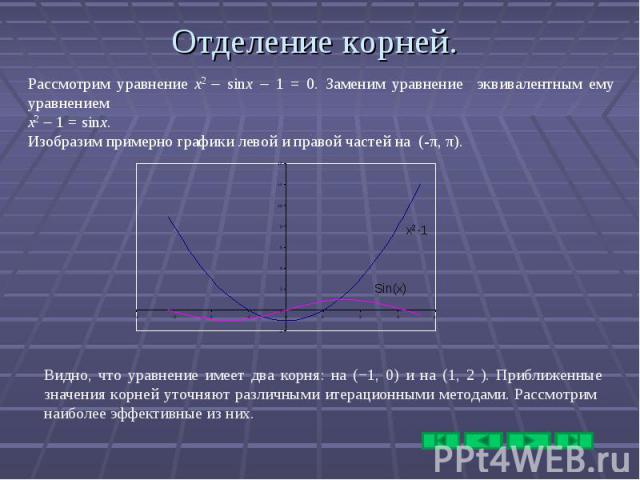
Отделение корней Отделение корней Метод дихотомии Метод простой итерации Метод Ньютона Метод хорд

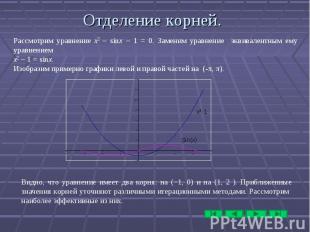
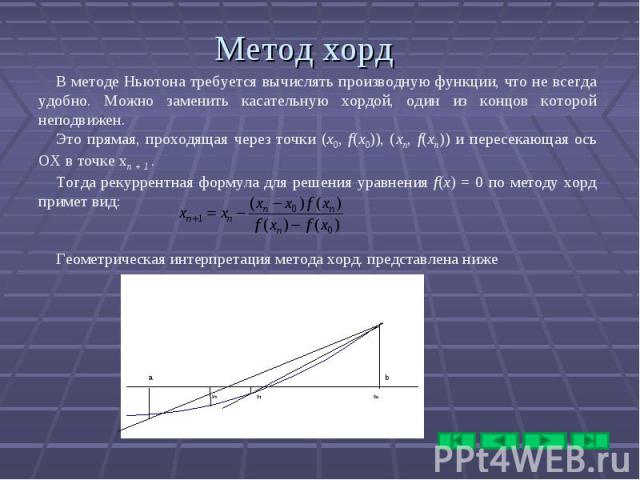
Пусть мы нашли такие точки a и b, что на отрезке [a, b] лежит единственный корень уравнения. Найдем середину отрезка c = (a+b)/2 и вычислим f(c). Из двух половин отрезка выберем ту, на концах которой функция имеет разные знаки, тогда корень лежит на этой половине. Затем новый отрезок опять делим пополам и т.д. Пусть мы нашли такие точки a и b, что на отрезке [a, b] лежит единственный корень уравнения. Найдем середину отрезка c = (a+b)/2 и вычислим f(c). Из двух половин отрезка выберем ту, на концах которой функция имеет разные знаки, тогда корень лежит на этой половине. Затем новый отрезок опять делим пополам и т.д. Если требуется найти корень с точностью ε, то продолжаем деление пополам до тех пор, пока длина отрезка не станет меньше 2ε. Тогда середина последнего отрезка даст значение корня с требуемой точностью. Дихотомия проста и очень надежна: к простому корню она сходится для любых непрерывных функций f(x); при этом она устойчива к ошибкам округления. Скорость сходимости невелика: за k итераций длина отрезка уменьшится в 2k раза (уточнение трех цифр требует 10 итераций). Погрешность метода на шаге k оценивается следующим образом: где ξ- точное решение уравнения, xk — значение одного из концов отрезка на шаге к. Дихотомия применяется тогда, когда требуется высокая надежность счета, а скорость сходимости малосущественна

Заменим уравнение f(x) = 0 эквивалентным ему уравнением х = φ(х), Заменим уравнение f(x) = 0 эквивалентным ему уравнением х = φ(х), где φ(х) ─ дифференцируемая функция. Это можно сделать многими способами, например, положив φ(х) ≡ x + ψ(x)f(x), где ψ(x) — произвольная непрерывная знакопостоянная функция. Выберем некоторое нулевое приближение х0 и вычислим дальнейшие приближения по формулам xn+1 = φ(xn), где n = 0, 1, 2, . . . (1) Исследуем условия сходимости. Если φ(х) имеет непрерывную производную, то: хn + 1 ξ = φ(хn) φ(ξ) = (хп ξ)φ'(θ), где точка θ лежит между точками хn и ξ. Поэтому, если всюду |φ'(х)| ≤ q < 1, то значения Іхп ξІ убывают не медленней членов геометрической прогрессии со знаменателем q < 1, и последовательность хп сходится при любом нулевом приближении. Если |φ'(ξ)| > 1, то, в силу непрерывности, |φ'(х)| больше единицы и в некоторой окрестности корня; в этом случае итерации не могут сходиться. Если |φ'(ξ)| < 1, но вдали от корня |φ'(х)| > 1, то итерации сходятся, если нулевое приближение выбрано достаточно близко к корню; при произвольном нулевом приближении сходимости может не быть. Очевидно, что чем меньше q, тем быстрей сходимость. Погрешность метода можно оценить соотношением: │хk ξ│ ≤ qk│х0 ξ│ где ξ ─ точное решение уравнения, xk ─ значение итерации на шаге k. Тогда количество итераций, необходимых для достижения точности ε, можно определить из неравенства: qk│х0 ξ│ < ε.

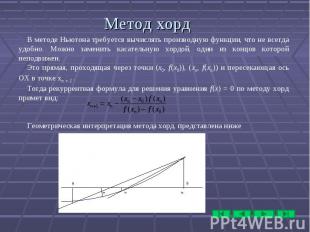
Пусть на [a, b] существует единственный корень уравнения f(x) = 0, f(x) – функция непрерывная вместе с первой производной на [a, b]. Заменим f(x) линейной функцией f(xn) + f′(xn)(x xn) ─ выражением для касательной в точке xn, принадлежащей отрезку [a, b]. Тогда точка пересечения графика этой функции с осью OX (решение уравнения f(xn) + f′(xn)(x xn) = 0) ─ очередное приближение к решению уравнения по методу Ньютона. Пусть на [a, b] существует единственный корень уравнения f(x) = 0, f(x) – функция непрерывная вместе с первой производной на [a, b]. Заменим f(x) линейной функцией f(xn) + f′(xn)(x xn) ─ выражением для касательной в точке xn, принадлежащей отрезку [a, b]. Тогда точка пересечения графика этой функции с осью OX (решение уравнения f(xn) + f′(xn)(x xn) = 0) ─ очередное приближение к решению уравнения по методу Ньютона. Отсюда, (2)

Теорема (о достаточных условиях сходимости метода Ньютона). Пусть выполняются следующие условия: 1.Функция f(x) определена и дважды непрерывно дифференцируема на [a, b]; 2.Отрезку [a, b] принадлежит только один простой корень (f(a) f(b) < 0) 3.Производные f (х), f (х) сохраняют знак на [a, b] и f (х) не обращается в 0; 4.Начальное приближение х0 удовлетворяет неравенству f(х0)·f (х0) ≥ 0. Тогда последовательность{xn} монотонно сходится к корню уравнения f(x) = 0. Скорость сходимости метода Ньютона квадратичная:|xk+1 ξ| ≤ C∙|xk ξ|2,где

Оценка погрешности При решении уравнения f(x) = 0 приближенным методом можно оценить погрешность следующим образом: пусть f (х) m на [a, b] , это справедливо, т.к. f (х) 0 и она непрерывна на [a, b]. Из │f(xn) f(ξ)│ = │f′(θ)│∙│xn ξ│ следует, что

Решение задач линейной алгебры Точные методы Метод Гаусса Пример Приближенные методы

Метод Гаусса

Пример

Приближенные методы Метод простой итерации Метод Якоби Метод Зейделя Пример

Метод простой итерации

Метод Якоби

Метод Зейделя

Пример

Интерполяция

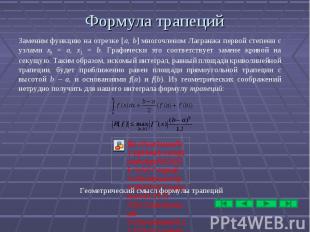
Постановка задачи Постановка задачи Формулы прямоугольников Формула трапеций Формула Симпсона Погрешность составных формул Пример

Постановка задачи

Формулы прямоугольников

Формула левых прямоугольников

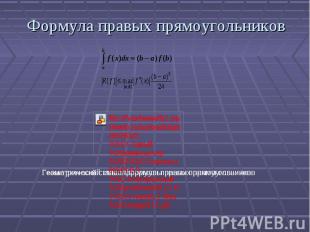
Формула правых прямоугольников

Формула средних прямоугольников

Составная формула Симпсона

Постановка задачи Постановка задачи Методы, основанные на разложении решения в ряд Тейлора Методы Рунге - Кутты Разностные методы Пример

Постановка задачи

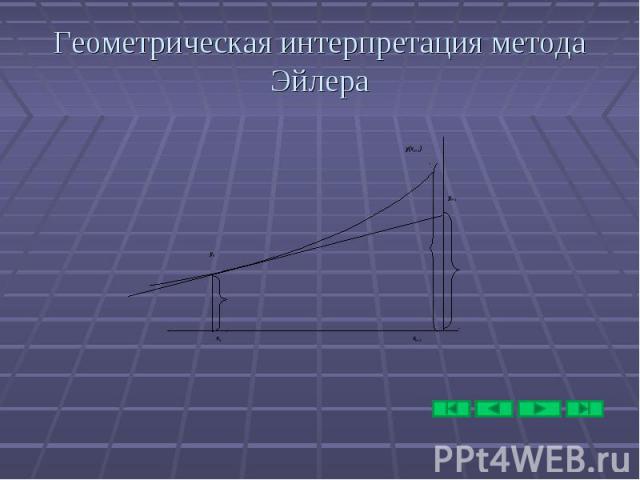
Геометрическая интерпретация метода Эйлера

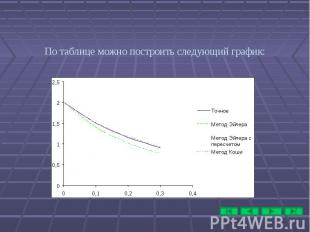
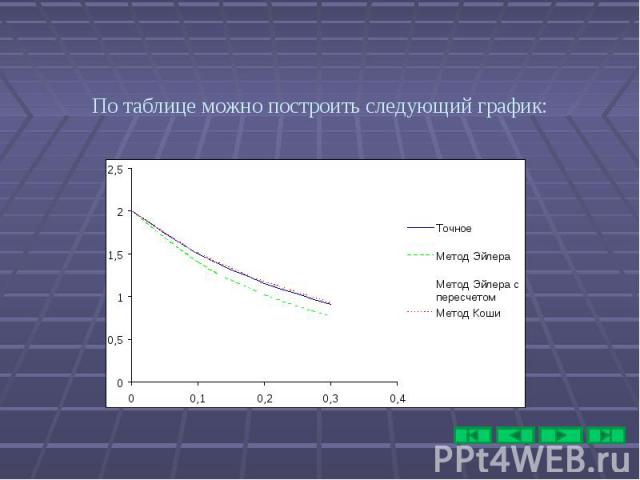
По таблице можно построить следующий график:

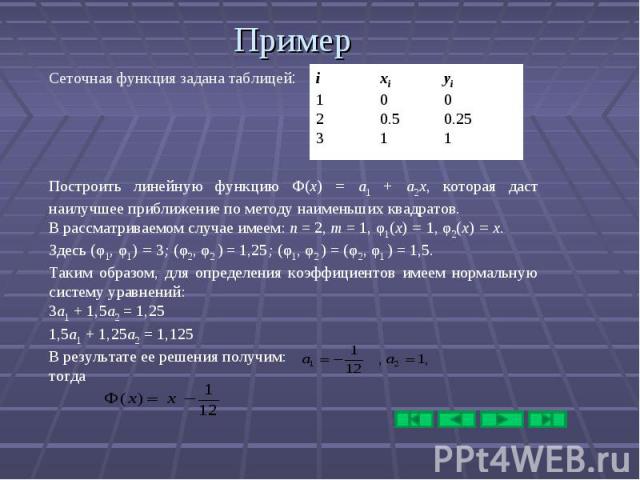
Пример

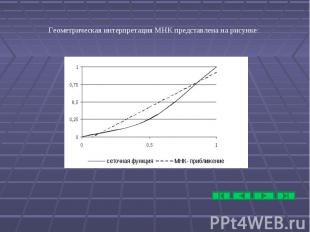
Литература Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. М.: БИНОМ, 2006. Вержбицкий В. М. Численные методы. М.: ОНИКС 21 век, 2005. Костомаров Д. П., Фаворский А. П. Вводные лекции по численные методам. М.: Логос, 2004. Киреев В. И., Пантелеев А. В. Численные методы в примерах и задачах. М.: Высшая школа, 2004. Бахвалов Н. С., Лапин А. В., Чижонков Е. В. Численные методы в задачах и упражнениях. М.: Высшая школа,2000.