Презентация на тему: Движение космических аппаратов

В.Г. Петухов E-mail: [email protected] Государственный космический научно-производственный центр им. М.В. Хруничева 900igr.net

СОДЕРЖАНИЕ ВВЕДЕНИЕ 1. МЕТОД ПРОДОЛЖЕНИЯ ПО ПАРАМЕТРУ 2. ОПТИМАЛЬНЫЕ МЕЖПЛАНЕТНЫЕ ПЕРЕЛЕТЫ КА С ИДЕАЛЬНО РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ 3. ОПТИМИЗАЦИЯ ТРАЕКТОРИИ ПЕРЕЛЕТА НА ОРБИТУ ВОКРУГ ЛУНЫ КА С ИДЕАЛЬНО РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ 4. ОПТИМИЗАЦИЯ МНОГОВИТКОВЫХ ПЕРЕЛЕТОВ МЕЖДУ ЭЛЛИПТИЧЕСКИМИ НЕКОМПЛАНАРНЫМИ ОРБИТАМИ КА С ДВИГАТЕЛЕМ ПОСТОЯННОЙ СКОРОСТИ ИСТЕЧЕНИЯ ЗАКЛЮЧЕНИЕ 2

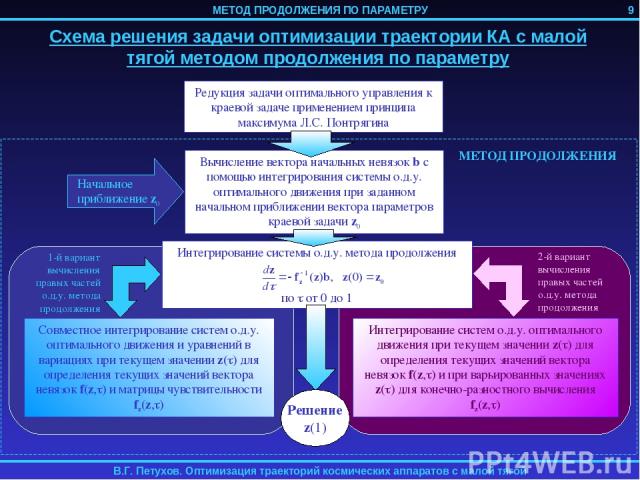
ВВЕДЕНИЕ Представлен единый методический подход к решению различных задач численной оптимизации траекторий КА с малой тягой. Основой этого подхода является формальная редукция краевой задачи принципа максимума к задаче Коши. Такая редукция достигается применением метода продолжения по параметру. 3

Оптимизация перелетов КА с малой тягой: Т.М. Энеев, В.А. Егоров, В.В. Белецкий, Г.Б. Ефимов, М.С. Константинов, Г.Г. Федотов, Ю.А. Захаров, Ю.Н. Иванов, В.В. Токарев, В.Н. Лебедев, В.В. Салмин, С.А. Ишков, В.В. Васильев, T.N. Edelbaum, F.W. Gobetz, J.P. Marec, N.X. Vinh, K.D. Mease, C.G. Sauer, C. Kluever, V. Coverstone-Carroll, S.N. Williams, M. Hechler и др. Метод продолжения: M. Kubicek, T.Y. Na и др. 4

Недостатки традиционных численных методов оптимизации малая область сходимости; вычислительная неустойчивость; необходимость подбора начального приближения в условиях отсутствия априорной информации о решении задачи. Часть этих явлений связана с физической сущностью задачи оптимизации (вопросы устойчивости, существования и ветвления решений). Однако, большинство численных методов вносят свои - методические - ограничения, не имеющие непосредственного отношения к свойствам математической задачи. Так, область сходимости практически всех численных методов существенно меньше области притяжения конкретной экстремальной точки в пространстве неизвестных параметров краевой задачи. Методические сложности связаны с вычислительной неустойчивостью и с ограниченностью области сходимости численных методов решения, а в некоторых случаях - например при использовании ряда прямых методов оптимизации - с большой размерностью задачи. 5

Цель разработки метода продолжения “Регуляризация” численной оптимизации траекторий, то есть устранение, по возможности, методических недостатков численной оптимизации. В частности, была поставлена и решена задача определения оптимальной траектории при использовании тривиального начального приближения (например, пассивного движения КА по начальной орбите). Рассматриваемые прикладные задач оптимизации траекторий 1. Оптимизация межпланетных траекторий КА с идеально регулируемым двигателем малой тяги; 2. Оптимизация траекторий перелета к Луне КА с идеально регулируемым двигателем малой тяги в рамках ограниченной задачи трех тел; 3. Оптимизация перелетов между некомпланарными эллиптическими орбитами КА с двигательной установкой с постоянной скоростью истечения. 6

7

8

9

2. ОПТИМАЛЬНЫЕ МЕЖПЛАНЕТНЫЕ ПЕРЕЛЕТЫ КА С ИДЕАЛЬНО РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ 10

11

2.2. УРАВНЕНИЯ ОПТИМАЛЬНОГО ДВИЖЕНИЯ (СЛУЧАЙ ПОСТОЯННОЙ МОЩНОСТИ) 12

13

14

15

16

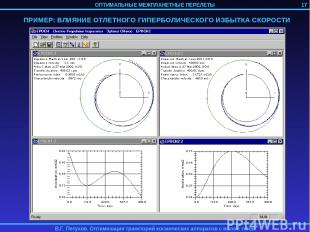
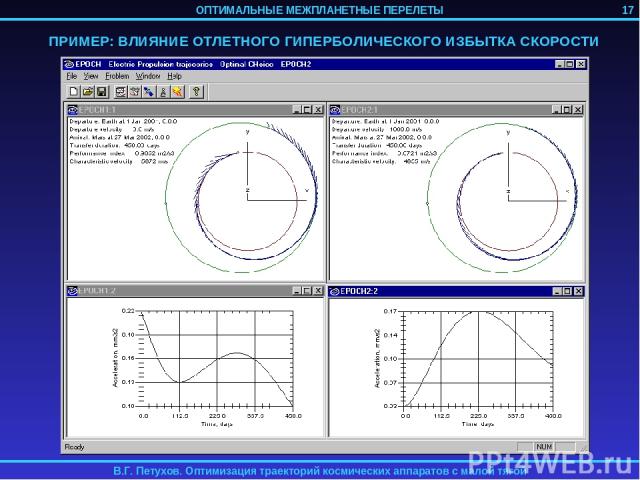
ПРИМЕР: ВЛИЯНИЕ ОТЛЕТНОГО ГИПЕРБОЛИЧЕСКОГО ИЗБЫТКА СКОРОСТИ 17

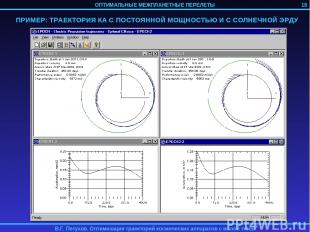
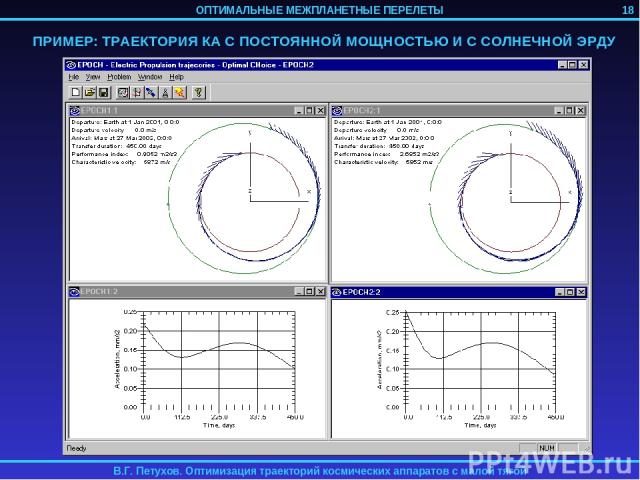
ПРИМЕР: ТРАЕКТОРИЯ КА С ПОСТОЯННОЙ МОЩНОСТЬЮ И С СОЛНЕЧНОЙ ЭРДУ 18

19

20

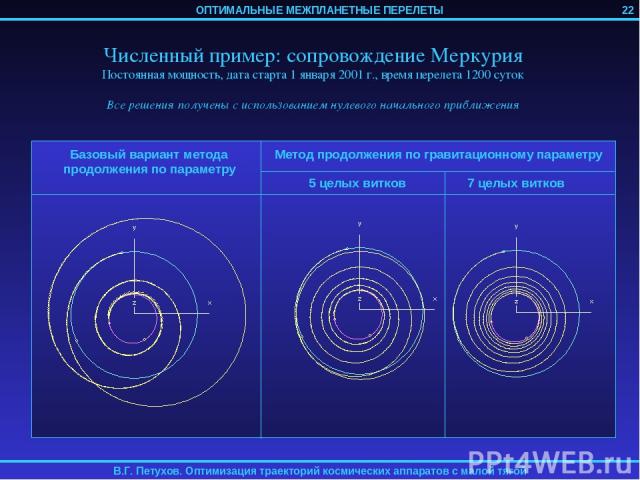
21

22

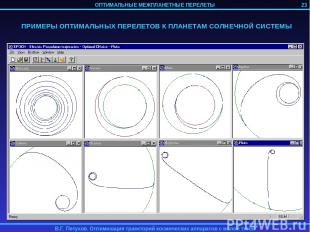
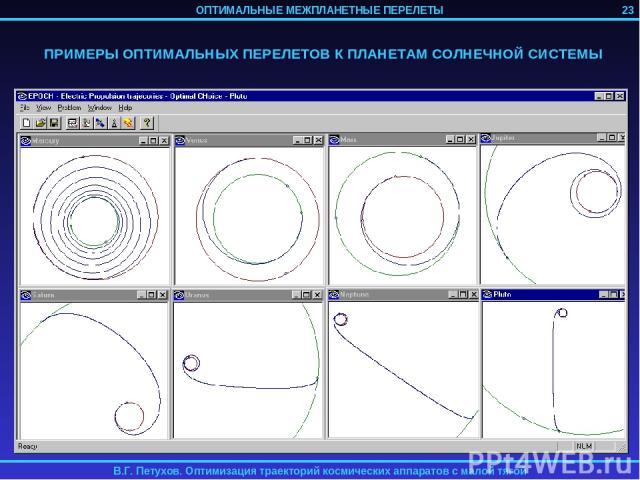
ПРИМЕРЫ ОПТИМАЛЬНЫХ ПЕРЕЛЕТОВ К ПЛАНЕТАМ СОЛНЕЧНОЙ СИСТЕМЫ 23

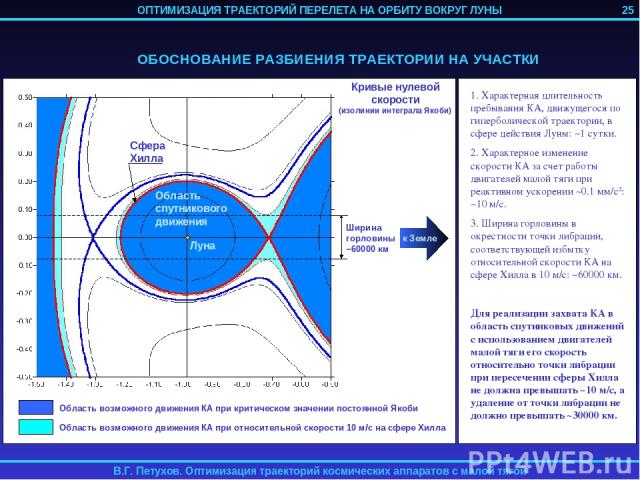
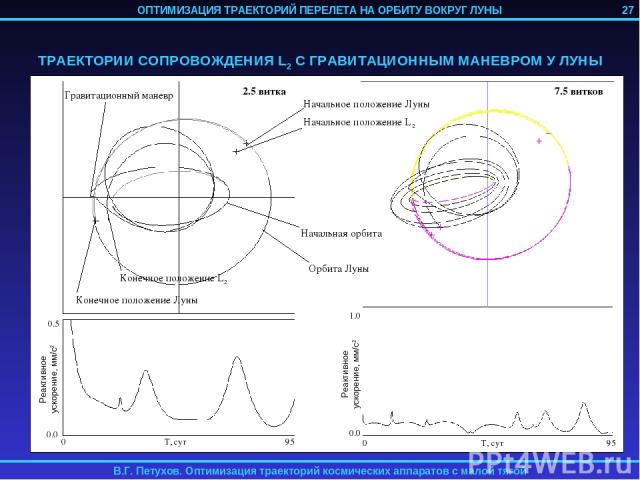
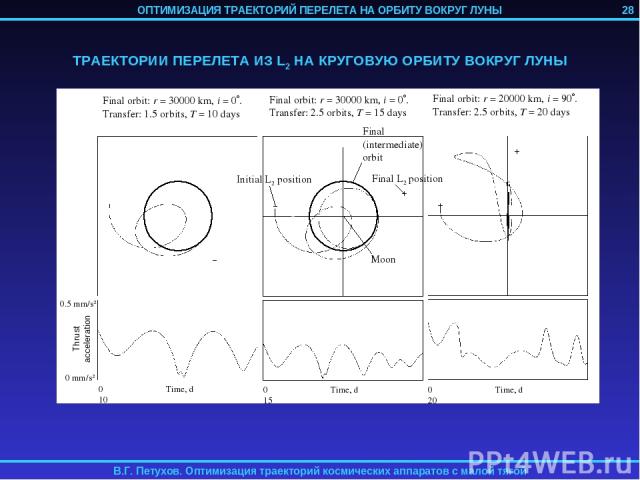
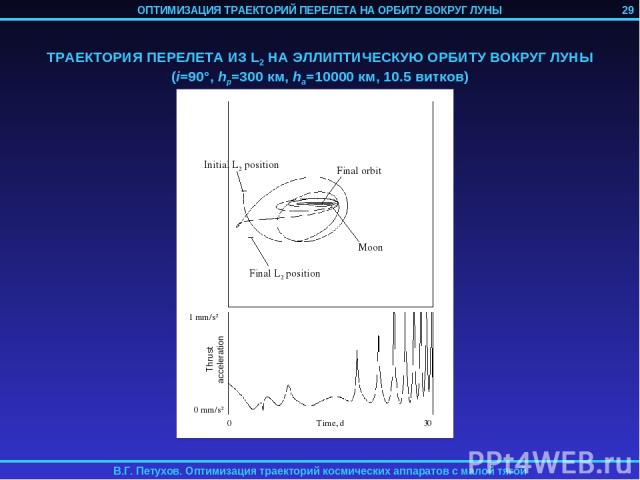
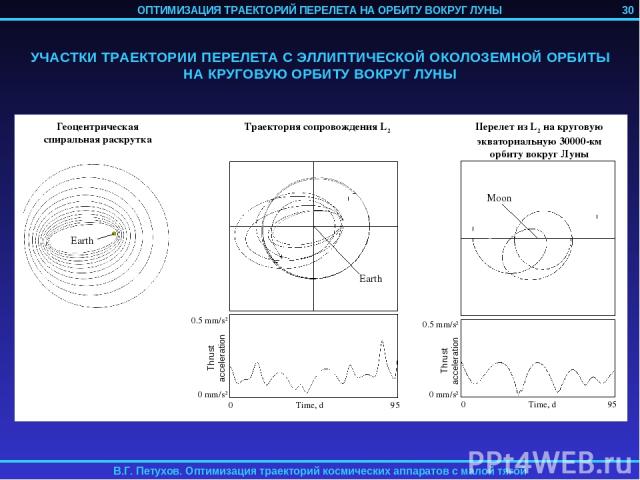
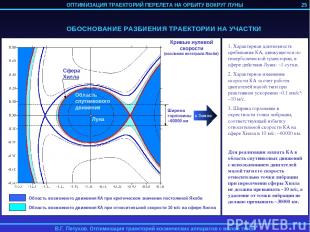
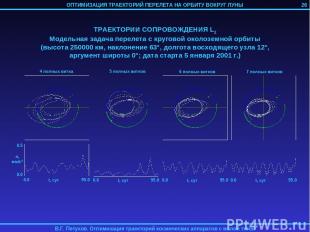
3. ОПТИМИЗАЦИЯ ТРАЕКТОРИИ ПЕРЕЛЕТА НА ОРБИТУ ВОКРУГ ЛУНЫ КА С ИДЕАЛЬНО РЕГУЛИРУЕМЫМ ДВИГАТЕЛЕМ МАЛОЙ ТЯГИ Рассматривается задача перелета КА с идеально регулируемым двигателем малой тяги с геоцентрической орбиты на орбиту спутника Луны. Траектория перелета разбивается на 4 участка: 1) Траектория геоцентрической спиральной раскрутки с начальной орбиты до некоторой промежуточной геоцентрической орбиты; 2) Траектория сопровождения точки либрации L2 системы Земля-Луна; 3) Траектория перелета из точки L2 на некоторую промежуточную селеноцентрическую орбиту; 4) Траектория селеноцентрической скрутки до целевой орбиты. 1-й и 4-й участок могут отсутствовать в случае достаточно высоких начальной геоцентрической и конечной селеноцентрической орбит. Траектории 2-го и 3-го участков определяются с помощью метода продолжения по параметру. 24

25

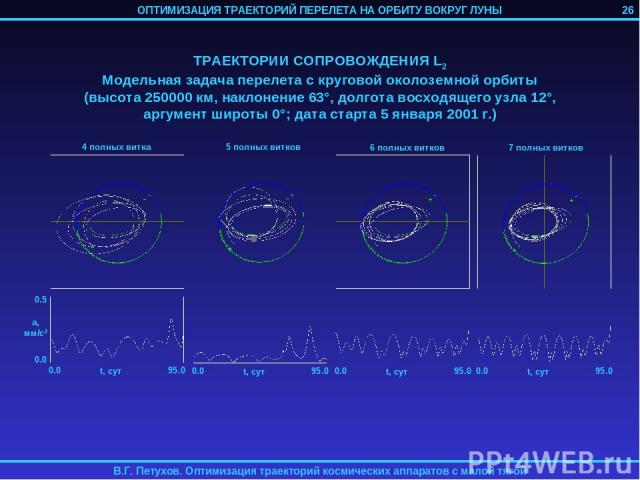
26

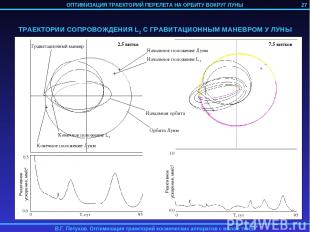
27

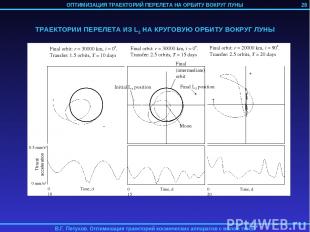
28

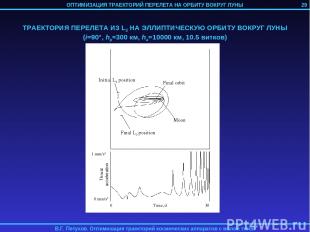
29

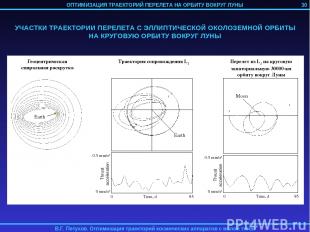
30

4. ОПТИМИЗАЦИЯ МНОГОВИТКОВЫХ ПЕРЕЛЕТОВ МЕЖДУ НЕКОМПЛАНАРНЫМИ ЭЛЛИПТИЧЕСКИМИ ОРБИТАМИ 31

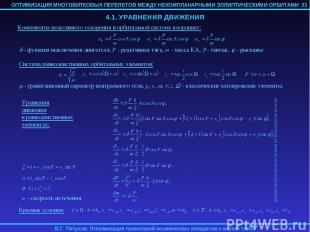
Уравнения орбитального движения КА записываются в равноденственных элементах, не имеющих особенностей при нулевом наклонении и эксцентриситете. Задача оптимального управления редуцируется к двухточечной краевой задаче применением принципа максимума Л.С. Понтрягина. Эта краевая задача, в свою очередь, формально редуцируется к задаче Коши с помощью метода продолжения по параметру. Для вычисления правых частей дифференциальных уравнений метода продолжения необходимо проинтегрировать систему дифференциальных уравнений оптимального движения (П-систему) и вычислить частные производные от конечного фазового вектора П-системы по начальным значениям сопряженных переменных. При численном интегрировании П-системы ее правые части численно осредняются по истинной долготе КА. Частные производные от конечного фазового вектора П-системы по начальным значениям сопряженных переменных определяются по конечно-разностным соотношениям. В результате первого интегрирования П-системы формируется вектор невязок решения краевой задачи. Для определения матрицы чувствительности с помощью конечных разностей требуется 6 дополнительных интегрирований П-системы. В результате, после решения системы линейных алгебраических уравнений формируется вектор правых частей системы дифференциальных уравнений метода продолжения. Система дифференциальных уравнений метода продолжения численно интегрируется по параметру продолжения от 0 до 1, в результате чего определяется оптимальное решения. 32

33

34

35

36

37

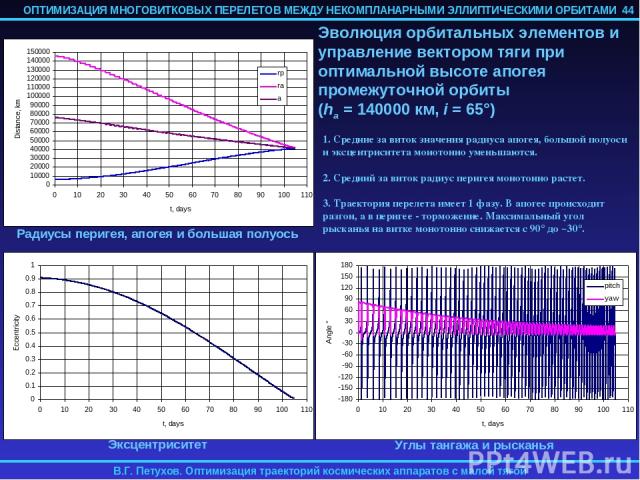
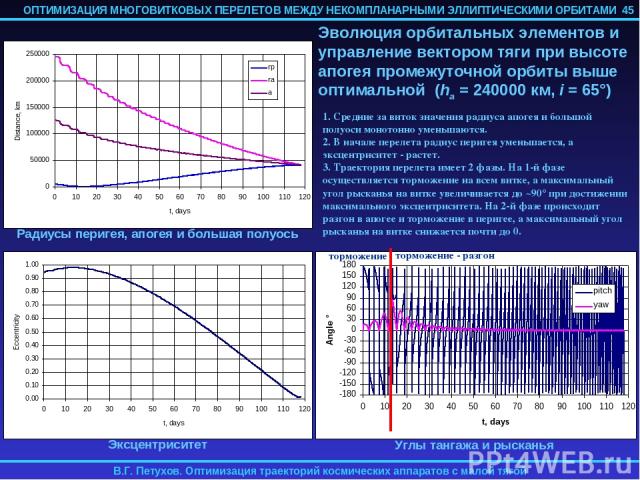
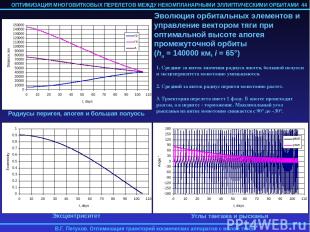
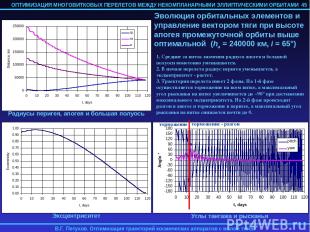
4.5. ОСОБЕННОСТИ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ Краевая задача решается методом продолжения по параметру. Для вычисления невязок f интегрируются осредненные по истинной долготе F уравнения оптимального движения. Эти уравнения имеют особенность при p=0, поэтому использовать нулевое начальное приближение для вектора сопряженных переменных нельзя. В задаче оптимального быстродействия при использовании метода продолжения по параметру в качестве начального приближения для p(0) выбиралось ph=1, если большая полуось конечной орбиты превышает большую полуось начальной орбиты и ph=-1 в противном случае. Остальные компоненты вектора p выбирались равными 0, а начальное приближение для безразмерного времени перелета T| =0=1 (в единицах начальной орбиты). С таким начальным приближением удалось решить задачи об оптимальном по быстродействию перелете с высокоэллиптической промежуточной орбиты (ПО) на ГСО при наклонении ПО 0°-75° и высоте апогея ПО 10000-120000 км. Если высота апогея ПО находилась вне этого диапазона, для решения задачи в качестве начального приближения приходилось использовать предварительно полученное решение задачи перелета с ПО с достаточно близкой высотой апогея. Осреднение уравнений оптимального движения по истинной долготе F осуществляется численно в процессе интегрирования этих уравнений. Вычисление частных производных от функции невязок f по параметрам краевой задачи p(0), T, необходимых для применения метода продолжения, производится также численно по конечно-разностным формулам первого порядка. Таким образом, для вычисления правых частей дифференциальных уравнений метода продолжение используется численное интегрирование численно осредненных уравнений оптимального движения и полученные численным дифференцированием частные производные от функции невязок краевой задачи по ее параметрам. 38

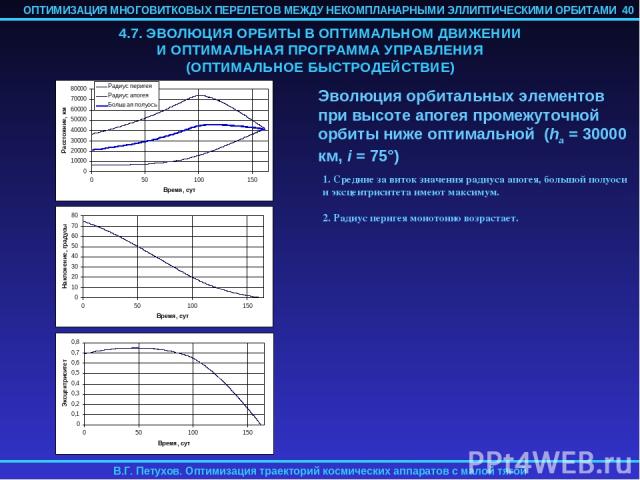
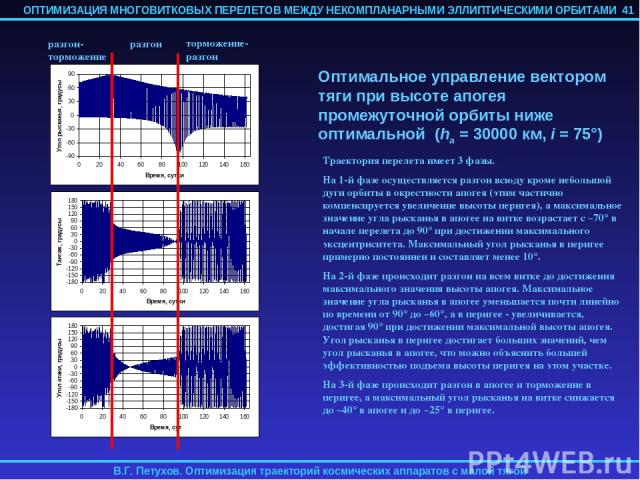
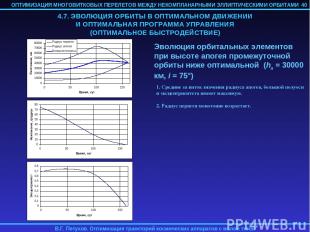
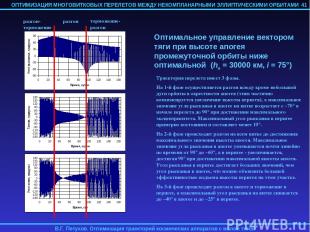
4.6. ОПТИМАЛЬНОЕ РЕШЕНИЕ В НЕОСРЕДНЕННОМ ДВИЖЕНИИ Малый уровень реактивного ускорения (по сравнению с гравитационным) обуславливает близость эволюции орбитальных элементов в осредненном и неосредненном движении в эллиптическом случае. Для проверки применимости найденного для осредненных уравнений движения оптимального управления, найденные оптимальные начальные значения параметров краевой задачи подставлялись в неосредненные уравнения оптимального движения, и эти уравнения численно интегрировались. Начальное значение истинной долготы F выбиралось достаточно произвольно (обычно соответствующее перигею или апогею начальной орбиты), а начальное значение сопряженной к ней переменной pF принималось равной 0 (см. замечание выше). В результате этого численного интегрирования определялись фактические невязки на правым конце траектории и программа оптимального управления. Для перелетов на ГСО с высокоэллиптических промежуточных орбит при уровне реактивного ускорения 0.1-0.5 мм/с2 разница в невязках при решении осредненной и неосредненной задач имела величину порядка 0.1%. Примеры использования оптимального управления, полученного для осредненной задачи к неосредненным уравнениям движения приводятся в следующем разделе. 39

40

41

42

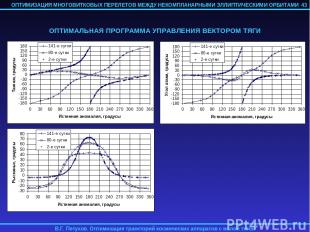
43

44

45

47

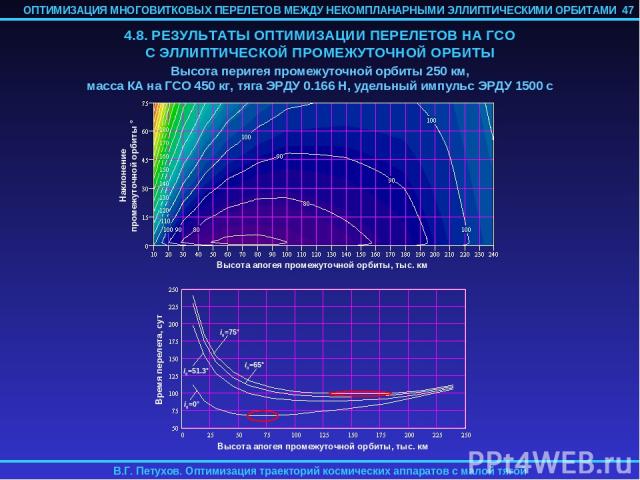
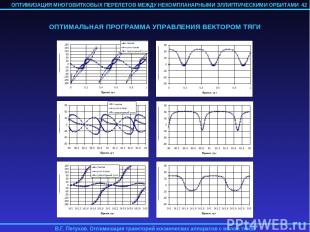
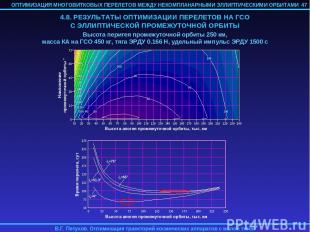
4.9. ВЫВОДЫ 1. Метод продолжения по параметру можно эффективно использовать для оптимизации многовитковых перелетов с малой тягой, что продемонстрировано на примере оптимизации по быстродействию перелетов с эллиптической промежуточной орбиты на ГСО. 2. В настоящее время не обнаружено каких-либо существенных ограничений на возможность использования разработанного метода в задачах с фиксированным временем и с различными краевыми условиями (межорбитальный перелет, набор заданной орбитальной энергии, разворот плоскости орбиты и т.д.). 3. Не обнаружено каких-либо ограничений на возможность учета внешних возмущающих сил при оптимизации траектории КА разработанным методом. Возмущающие силы, выраженные как через орбитальные элементы, так и через фазовый вектор КА, относительно легко могут быть введены в уравнения разработанного метода так как операции осреднения уравнений движения и вычисления производных от невязок краевой задачи по ее параметрам реализованы в рамках этого метода численно. Для учета возмущающих ускорений в уравнениях движения необходимы выражения для частных производных первого порядка от компонент этих ускорений по орбитальным элементам. 4. Разработанный метод позволил провести исчерпывающий анализ оптимальных по быстродействию перелетов с эллиптической промежуточной орбиты на ГСО, включая анализ влияния параметров промежуточной орбиты и основных проектных параметров КА на характеристики перелета и определение номинальных программ управления вектором тяги электроракетной двигательной установки КА. 48

49 ЗАКЛЮЧЕНИЕ Разработанный метод продолжения показал высокую эффективность для задачи оптимизации траекторий КА с идеально регулируемым двигателем малой тяги. Комбинация двух вариантов метода продолжения - базового метода и метода продолжения по гравитационноиу параметру - позволяет быстро и исчерпывающе проводить анализ межпланетных траекторий. С использованием метода продолжения были оптимизированы траектории КА с малой тягой, оканчивающиеся или начинающиеся в точке либрации L2 системы Земля-Луна. Эти траектории использовались для построения квазиоптимальных траекторий перелета между орбитами искусственных спутников Земли и Луны. Специально разработанная версия метода продолжения позволила провести полномасштабный анализ оптимальных по быстродействию пространственных траекторий перелета КА с малой тягой с эллиптической промежуточной орбиты на ГСО. Таким образом, характеристики метода продолжения делают его полезным и эффективным инструментом анализа траекторий КА с ЭРДУ.