Презентация на тему: Корень n-ой степени

МОУ лицей №10 города Советска Калининградской области учитель математики Разыграева Татьяна Николаевна Понятие корня n – й степени из действительного числа. 900igr.net

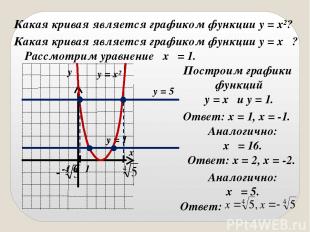
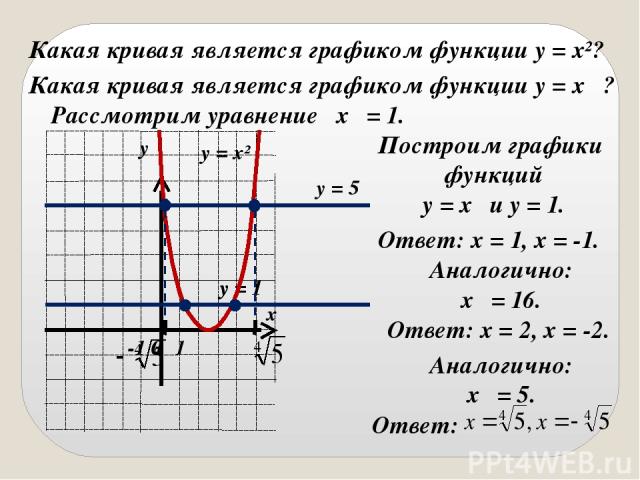
Какая кривая является графиком функции y = x²? Какая кривая является графиком функции y = x⁴ ? Рассмотрим уравнение x⁴ = 1. Построим графики функций y = x⁴ и y = 1. Ответ: x = 1, x = -1. Аналогично: x⁴ = 16. Ответ: x = 2, x = -2. Аналогично: x⁴ = 5. y = 5 Ответ:

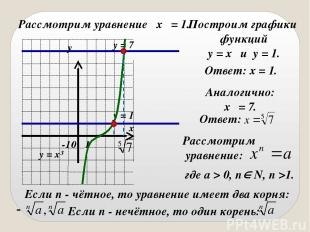
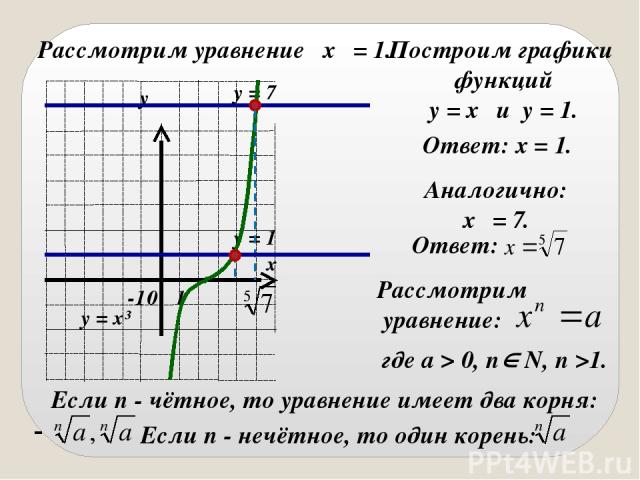
Рассмотрим уравнение x⁵ = 1. Построим графики функций y = x⁵ и y = 1. Аналогично: x⁵ = 7. Ответ: x = 1. Ответ: Рассмотрим уравнение: где a > 0, n N, n >1. Если n - чётное, то уравнение имеет два корня: Если n - нечётное, то один корень:

Определение 1 : Корнем n – й степени из неотрицательного числа a (n = 2,3,4,5,…) называют такое неотрицательное число, которое при возведении в степень n даёт в результате число a. Это число обозначают: a n - подкоренное выражение -показатель корня Операцию нахождения корня из неотрицательного числа называют извлечением корня. Если a 0, n = 2,3,4,5,…, то

Операция извлечение корня является обратной по отношению к возведению в соответствующую степень. 5² = 25 10³ = 1000 0,3⁴ = 0,0081 25 = 5 3 4 Иногда выражение a называют радикалом от латинского слова radix – «корень». n Символ - это стилизованная буква r. Возведение в степень Извлечение корня

Пример 1: Вычислить: а) 49; б) 0,125; в) 0 ; г) 17 3 7 4 Решение: а) 49 = 7, так как 7 > 0 и 7² = 49; 3 б) 0,125 = 0,5, так как 0,5 > 0 и 0,5³ = 0,125; в) 0 ; г) 17 ≈ 2,03 4 Определение 2 : Корнем нечётной степени n из отрицательного числа a (n = 3,5,…) называют такое отрицательное число, которое при возведении в степень n даёт в результате число a.

Итак Вывод: Корень чётной степени имеет смысл (т.е. определён) только для неотрицательного подкоренного выражения; корень нечётной степени имеет смысл для любого подкоренного выражения. Пример 2: Решите уравнения: Если a < 0, n = 3,5,7,…, то

Возведём обе части уравнения в куб: а) б) Возведём обе части уравнения в четвёртую степень: в) Решений нет. Почему? г) Возведём обе части уравнения в шестую степень:

Домашнее задание: § 39, № 1067, 1071, 1076, 1078. Удачи!!!!!