Презентация на тему: Функция в математике

Что такое «функция» Координатная плоскость Что такое «график функции» Декартова координатная плоскость История создания Линейная функция Функция у=кх прямая пропорциональность Обратная пропорциональность прямая пропорциональность Функция у=√х Функция у=х²

-термин, используемый в математике для обозначения такой зависимости между двумя величинами, при которой если одна величина задана, то другая может быть найдена. Обычно функция (с 17 в.) задается формулой, выражающей зависимую переменную через одну или несколько независимых переменных. -термин, используемый в математике для обозначения такой зависимости между двумя величинами, при которой если одна величина задана, то другая может быть найдена. Обычно функция (с 17 в.) задается формулой, выражающей зависимую переменную через одну или несколько независимых переменных. Функцию можно изобразить графически, нанося точки, координатами которых служат независимые и зависимые переменные, на координатную плоскость

- ЭТО Плоскость, на которой задана система координат. - ЭТО Плоскость, на которой задана система координат. Каждой точке на координатной плоскости соответствует пара чисел: её абсцисса и ордината. Наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами. Идея задавать положение точки на плоскости зародилась в древности – прежде всего у астрономов. Во II в. Древнегреческий астроном  Клавдий Птоломей пользовался широтой и долготой в качестве координат. Описание применения координат дал в книге «Геометрия» в 1637 г. французский математик Рене Декарт, поэтому прямоугольную систему координат часто называют декартовой.

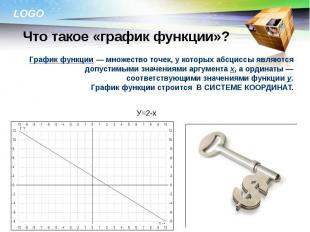
График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты — соответствующими значениями функции y. График функции строится В СИСТЕМЕ КООРДИНАТ.

Наиболее простая и поэтому часто используемая система координат на плоскости и в пространстве. Наиболее простая и поэтому часто используемая система координат на плоскости и в пространстве. Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X'X и Y'Y. Оси координат пересекаются в точке O, которая называется началом координат. Она делится на 4 четверти .

Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.

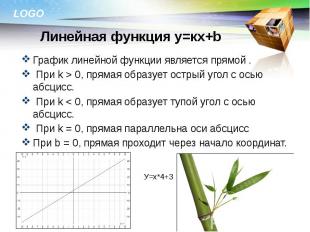
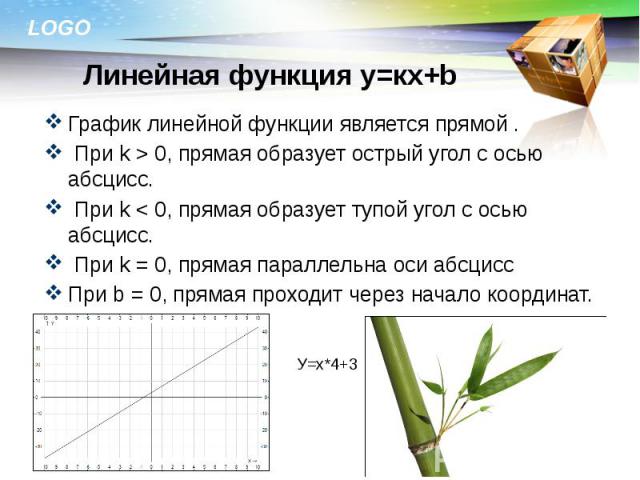
График линейной функции является прямой . График линейной функции является прямой . При k > 0, прямая образует острый угол с осью абсцисс. При k < 0, прямая образует тупой угол с осью абсцисс. При k = 0, прямая параллельна оси абсцисс При b = 0, прямая проходит через начало координат.

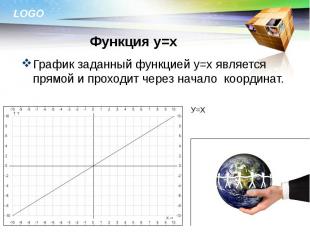
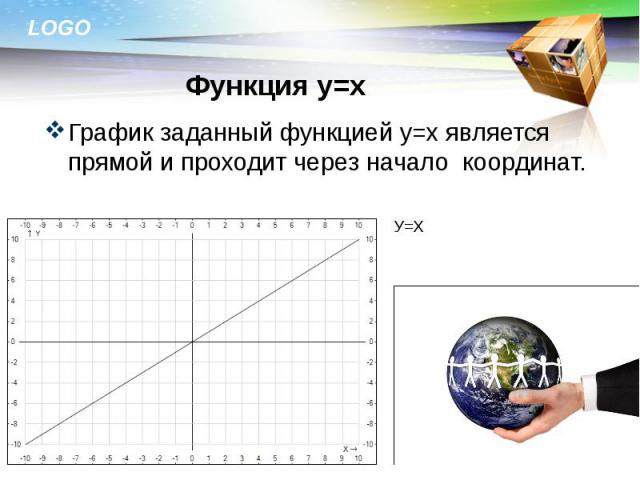
График заданный функцией у=х является прямой и проходит через начало координат. График заданный функцией у=х является прямой и проходит через начало координат.

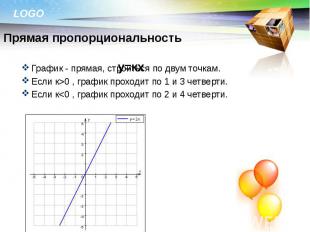
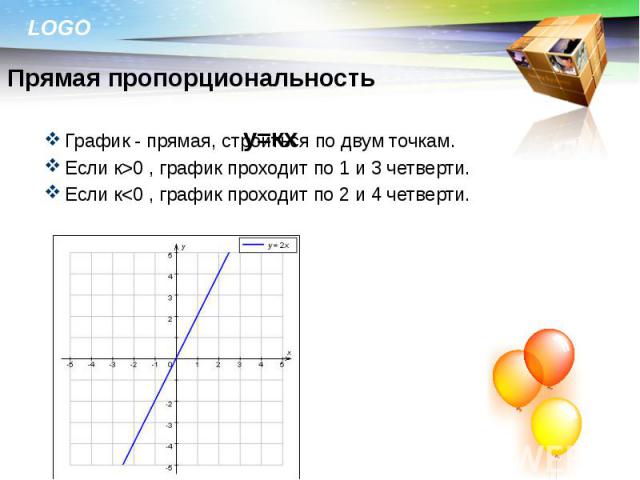
График - прямая, строиться по двум точкам. График - прямая, строиться по двум точкам. Если к>0 , график проходит по 1 и 3 четверти. Если к<0 , график проходит по 2 и 4 четверти.

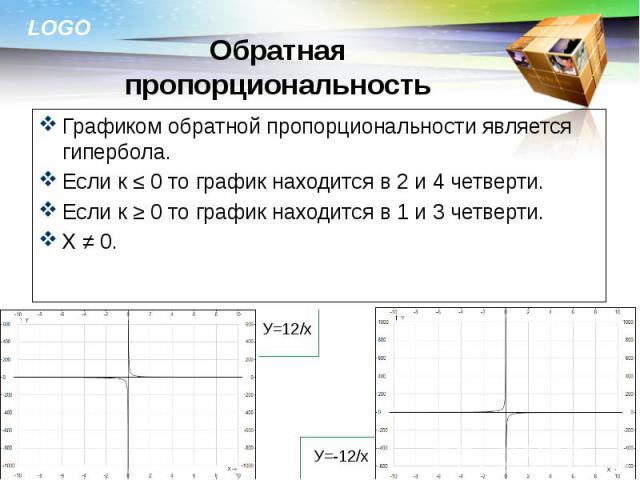
Графиком обратной пропорциональности является гипербола. Графиком обратной пропорциональности является гипербола. Если к ≤ 0 то график находится в 2 и 4 четверти. Если к ≥ 0 то график находится в 1 и 3 четверти. Х ≠ 0.

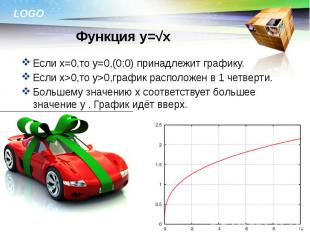
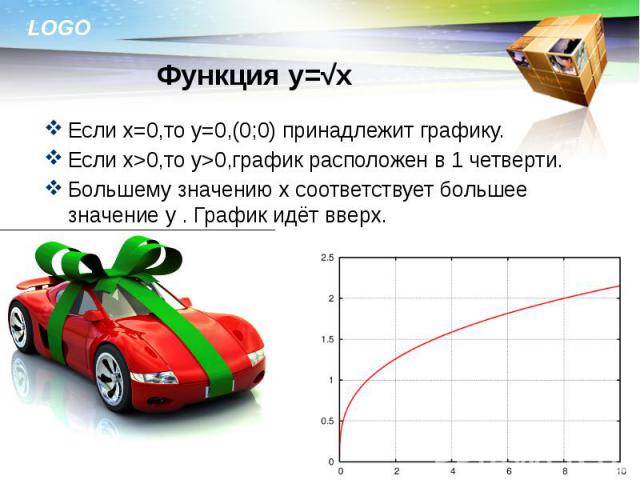
Если х=0,то у=0,(0;0) принадлежит графику. Если х=0,то у=0,(0;0) принадлежит графику. Если х>0,то у>0,график расположен в 1 четверти. Большему значению х соответствует большее значение у . График идёт вверх.

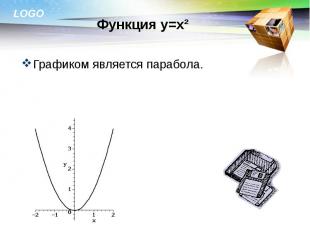
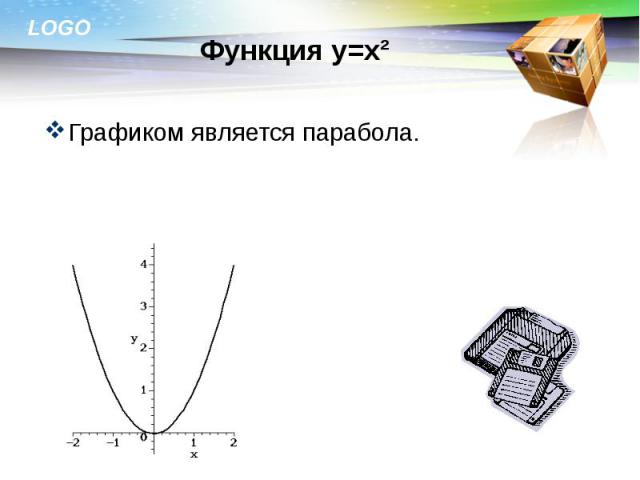
Графиком является парабола. Графиком является парабола.