Презентация на тему: Графики поверхностей и графики кривых в пространстве

Графики поверхностей и графики кривых в пространстве Лекция 6.

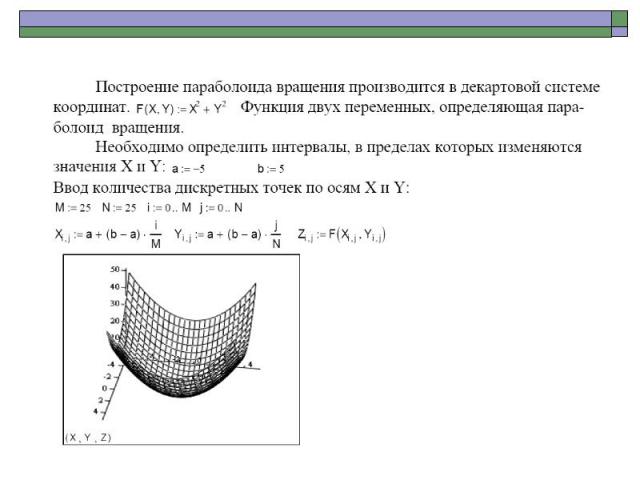
Построение поверхностей, заданных в явном виде в декартовой системе координат

Задана функция f(x,y)=sin(x2+y2). Постройте график соответствующей поверхности В соответствующем поле ввода на графике в качестве аргумента следует указать массив значений функции Mi,j=f(xi,yj) как матрицу соответствующих значений аппликат.

Постройте изображение эллипсоида Для построения поверхности, заданной при помощи параметров, следует знать, что MathCad интерпретирует поверхность как аппликаты точек соответствующей функции абсцисс и ординат. Поэтому вначале следует задать соответствующие значения трех матриц, определяя их как функции дискретных параметров в заданном диапазоне. При этом следует следить за тем, чтобы эти матрицы обязательно имели одинаковое число строк и столбцов. После этого достаточно напечатать имена этих трех матриц в поле ввода графической области. Рис 2. Изображение сферы

Построение поверхностей в сферической и цилиндрической системах координат

Связь между декартовой системой координат и сферической определяется формулами: Y = Rcos(α )sin(φ ) X = Rcos(α ) cos(φ ) Z = Rsin(α ) .

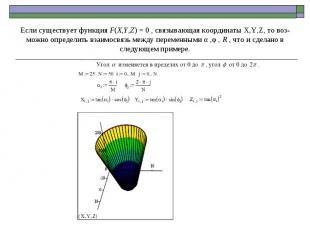
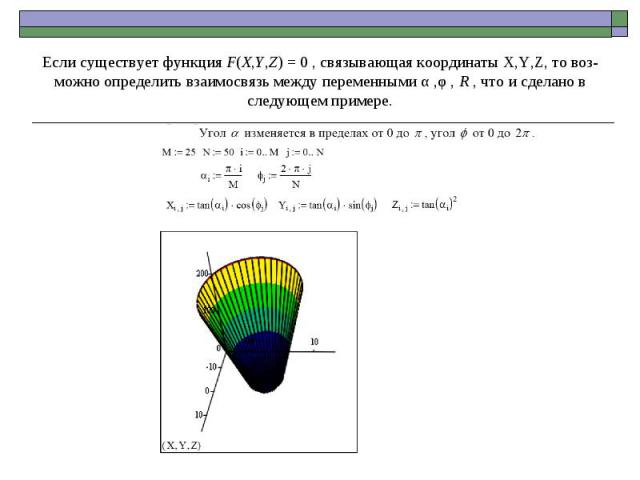
Если существует функция F(X,Y,Z) = 0 , связывающая координаты X,Y,Z, то воз- можно определить взаимосвязь между переменными α ,φ , R , что и сделано в следующем примере.

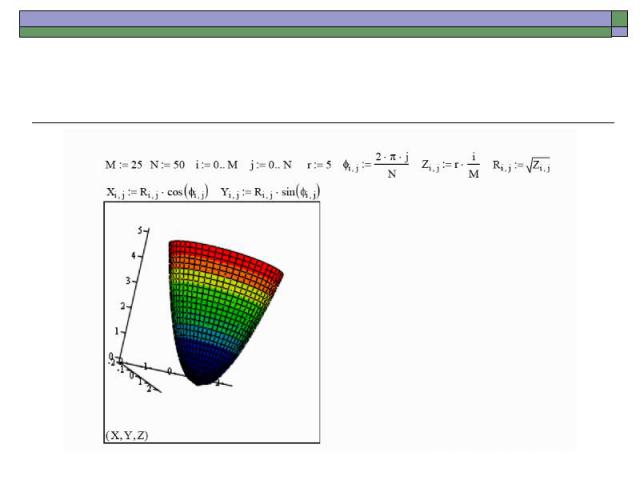
Связь между декартовой и цилиндрической системами координат выражается формулами: Y = r sin(φ ) X = rсos(φ ) Z = Z .

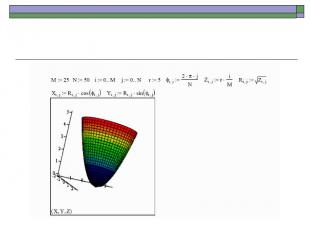
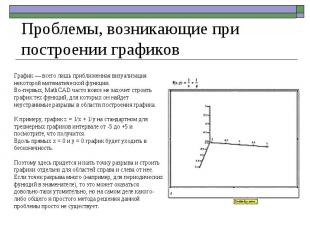
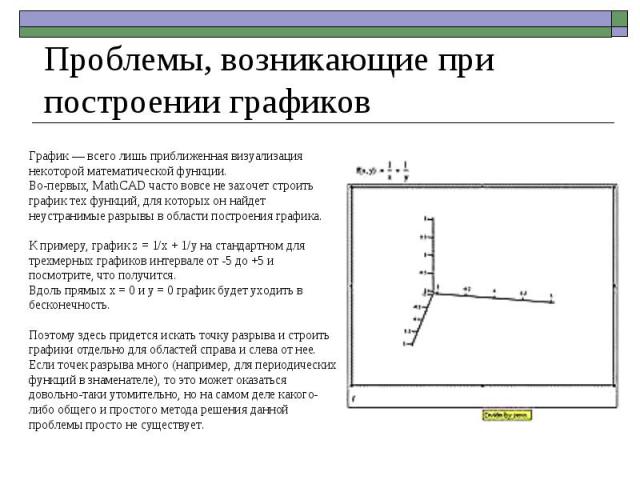
График — всего лишь приближенная визуализация некоторой математической функции. Во-первых, MathCAD часто вовсе не захочет строить график тех функций, для которых он найдет неустранимые разрывы в области построения графика. К примеру, график z = 1/x + 1/y на стандартном для трехмерных графиков интервале от -5 до +5 и посмотрите, что получится. Вдоль прямых x = 0 и y = 0 график будет уходить в бесконечность. Поэтому здесь придется искать точку разрыва и строить графики отдельно для областей справа и слева от нее. Если точек разрыва много (например, для периодических функций в знаменателе), то это может оказаться довольно-таки утомительно, но на самом деле какого-либо общего и простого метода решения данной проблемы просто не существует. Проблемы, возникающие при построении графиков

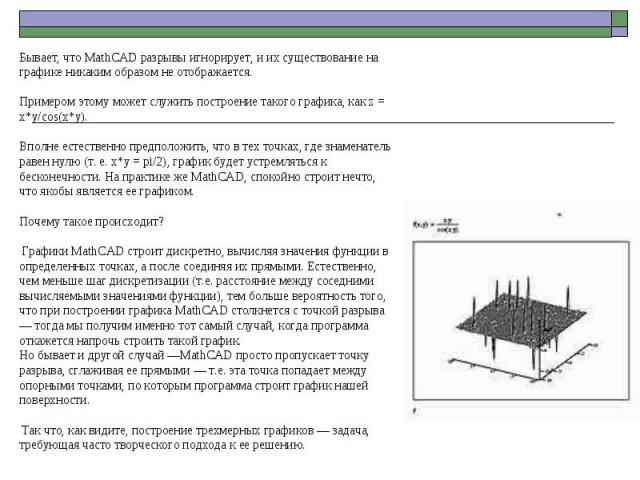
Бывает, что MathCAD разрывы игнорирует, и их существование на графике никаким образом не отображается. Примером этому может служить построение такого графика, как z = x*y/cos(x*y). Вполне естественно предположить, что в тех точках, где знаменатель равен нулю (т. е. x*y = pi/2), график будет устремляться к бесконечности. На практике же MathCAD, спокойно строит нечто, что якобы является ее графиком. Почему такое происходит? Графики MathCAD строит дискретно, вычисляя значения функции в определенных точках, а после соединяя их прямыми. Естественно, чем меньше шаг дискретизации (т.е. расстояние между соседними вычисляемыми значениями функции), тем больше вероятность того, что при построении графика MathCAD столкнется с точкой разрыва — тогда мы получим именно тот самый случай, когда программа откажется напрочь строить такой график. Но бывает и другой случай —MathCAD просто пропускает точку разрыва, сглаживая ее прямыми — т.е. эта точка попадает между опорными точками, по которым программа строит график нашей поверхности. Так что, как видите, построение трехмерных графиков — задача, требующая часто творческого подхода к ее решению.

Функция CreateMesh Использование функции CreateMesh предполагает параметризацию той поверхности, которую вы хотите визуализировать с использованием MathCAD\'а. Итак, во-первых, нужно задать три функции, описывающие зависимость каждой из координат (x, y, z) от двух параметров (с другим числом параметров MathCAD работать не умеет). Для определенности положим, что параметры у нас будут a и b. После того, как функциональная зависимость задана, функции x(a,b), y(a,b) и z(a,b) нужно сгруппировать в вектор-столбец. Напомню, что для этого нужно создать с помощью кнопки Matrix or Vector, расположенной на панели инструментов Matrix, матрицу размером 3 на 1, в элементы которой и вписать указанные функции. Далее добавляем на рабочую область MathCAD поле трехмерного графика, внизу которого пишем следующее (без кавычек): \"CreateMesh(f, 0, 10, 0, 10, 50, 50)\". Результаты построение одной из возможных параметрических поверхностей вы можете увидеть на рисунке. Давайте теперь разберемся с параметрами, которые указаны для функции CreateMesh. Первым стоит имя нашего вектора с функциями. После имени вектора идут соответственно минимальное и максимальное значения для первого и второго параметров. Далее идут два параметра, указывающие MathCAD, на сколько шагов разбить указанный диапазон для построения точек, по которым уже будет чертиться собственно график.

Все параметры, кроме имени вектора, описывающего поверхность, являются необязательными. Для того, чтобы показать всю простоту и мощь применения CreateMesh, приведу еще один пример, а именно построение с помощью данной функции сферы. Для этого нужно задать следующие уравнения в описанном выше примере: x(a,b) := sin(a)*cos(b); y(a,b) := sin(a)*sin(b); z(a,b) := cos(a). Кроме того, нужно поменять также и диапазоны, в которых будут изменяться a и b: первый параметр будет меняться от нуля до двух пи, второй — от нуля до пи. Результат построения сферы вы также можете увидеть на соответствующем рисунке.

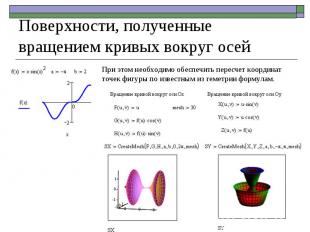
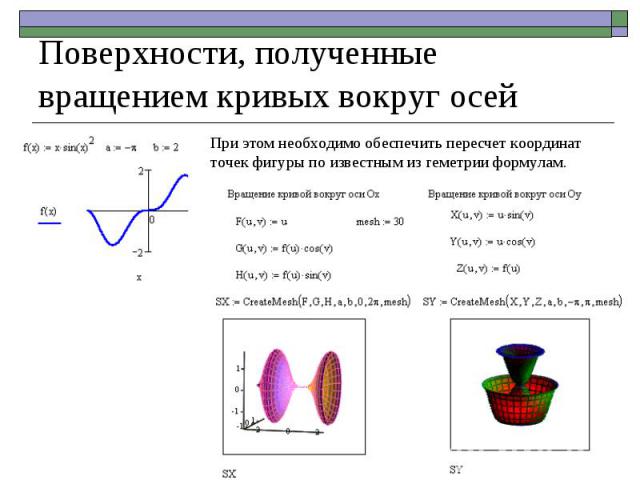
При этом необходимо обеспечить пересчет координат точек фигуры по известным из геметрии формулам. Поверхности, полученные вращением кривых вокруг осей

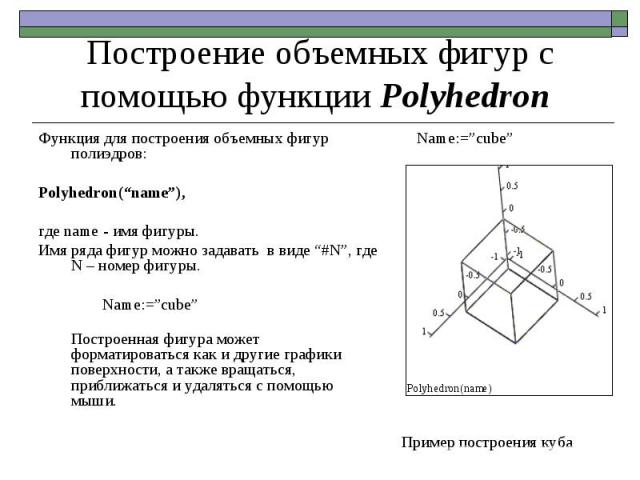
Пример построения куба Name:=”cube” Построение объемных фигур с помощью функции Polyhedron Функция для построения объемных фигур полиэдров: Polyhedron(“name”), где name - имя фигуры. Имя ряда фигур можно задавать в виде “#N”, где N – номер фигуры. Name:=”cube” Построенная фигура может форматироваться как и другие графики поверхности, а также вращаться, приближаться и удаляться с помощью мыши.

Аргументом функции является строка с именем, номером фигуры или с ее описателем в случае создания составных полиэдров. Всего в таблице имеется около 60 полиэдров. Большое число примеров применения функции PolyLookup можно найти в справочной системе Matchad – раздел Polyhedra таблиц Reference Table. Функция задания полиэдров PolyLookup Для описания произвольных полиэдров в Mathcad Professional служит функция PolyLookup, которую можно задать одним из следующих способов: PolyLookup(“имя\") PolyLookup(“#N”) Ро1уLооkuр(“0писатель”).

Функция задания полиэдров PolyLookupДля описания произвольных полиэдров в Mathcad Professional служит функция PolyLookup, которую можно задать одним из следующих способов:PolyLookup(“имя")PolyLookup(“#N”)Ро1уLооkuр(“0писатель”).