Презентация на тему: Гэксаедр

Подготовили: ученики 11 класса Драгунов Игорь и Франк Татьяна Тема:«Многогранники.Икосаэдр»

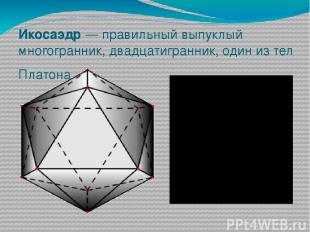
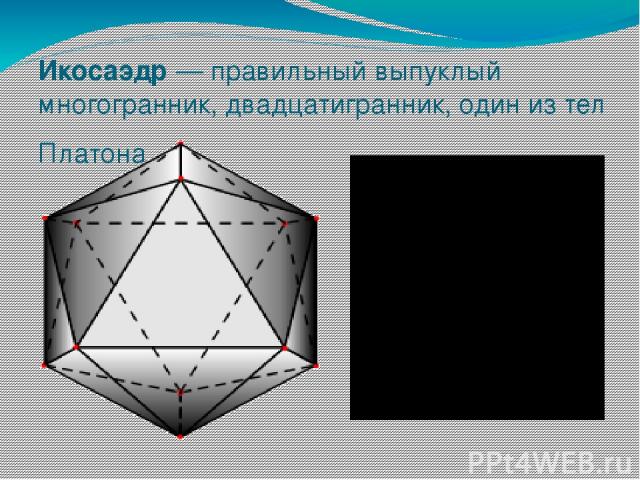
Икосаэдр — правильный выпуклый многогранник, двадцатигранник, один из тел Платона. 

Все 20 граней являются равносторонними треугольниками. количество ребер соответствует 30, количество вершин — 12. Икосаэдр состоит из 59 звёздчатых форм.   Все 12 вершин икосаэдра являются вершинами 5 равносторонних Треугольников, значит, сумма углов у вершины = 300°. У икосаэдра 30 ребер. Как и у всех правильных многогранников ребра икосаэдра имеют равную длину, а грани - равную площадь.

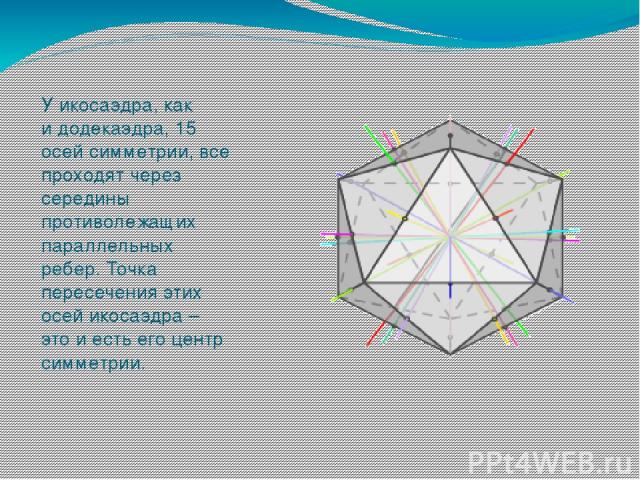
У икосаэдра, как и додекаэдра, 15 осей симметрии, все проходят через середины противолежащих параллельных ребер. Точка пересечения этих осей икосаэдра – это и есть его центр симметрии.

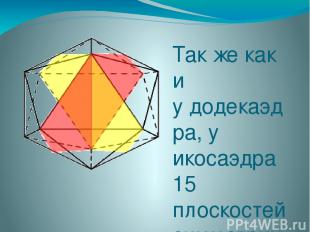
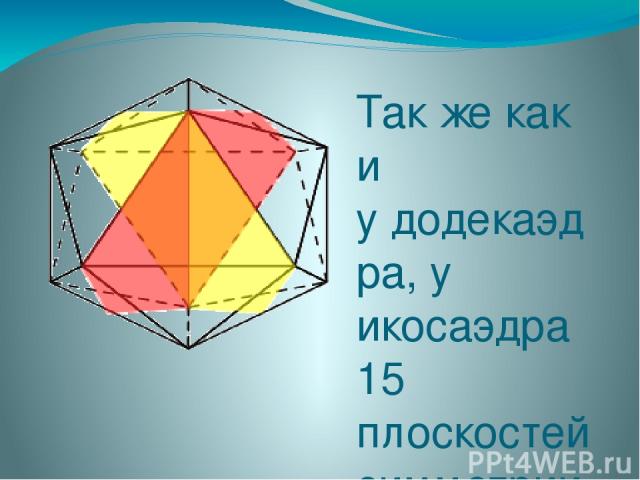
Так же как и у додекаэдра, у икосаэдра 15 плоскостей симметрии. Плоскости симметрии проходят через четыре вершины, которые лежат в одной плоскости, и середины противоположных параллельных ребер. 

Пусть длина ребра икосаэдра будет а тогда:   Сумма длин всех ребер: P = 30a    Площадь икосаэдра:     Объем икосаэдра:     Радиус вписанной в икосаэдр сферы:     Радиус описанной вокруг икосаэдра сферы:  

Свойства икосаэдра.   1. Каждая из 12 вершин икосаэдра лежит по 3 в 4-х параллельных плоскостях, образуя во всех плоскостях правильный треугольник. 2. 10 вершин икосаэдра находятся в 2-х параллельных плоскостях, и образуют в них 2 правильных 5-ти угольника, а оставшиеся 2 — противоположны друг другу и находятся в 2-х концах диаметра описанной вокруг икосаэдра сферы, который перпендикулярен параллельным плоскостям. 3. Икосаэдр возможно вписать в куб, тогда 6 взаимо-перпендикулярных ребер икосаэдра будут находиться соответственно на 6-ти гранях куба, оставшиеся 24 ребра находятся внутри куба, все 12 вершин икосаэдра будут находиться на ше6-ти гранях куба. 4. В икосаэдр можно вписать тетраэдр, таким образом, чтобы 4 вершины тетраэдра станут совмещены с 4-мя вершинами икосаэдра. 5. Икосаэдр возможно вписать в додекаэдр, тогда вершины икосаэдра совместятся с центрами граней додекаэдра.

В икосаэдр возможно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра. Усечённый икосаэдр можно получить, срезав 12 вершин с образованием граней вида правильных 5-ти угольников. Тогда количество вершин нового многогранника увеличится в 5 раз (12×5=60), 20 треугольных граней становятся правильными шестиугольниками (количество граней теперь 20+12=32), а рёбер - 30+12×5=90. Сделать икосаэдра можно из 20 тетраэдров. Нельзя сделать икосаэдр из правильных тетраэдров, потому что радиус описанной сферы вокруг икосаэдра и длина бокового ребра (вершины-центр такой сборки) тетраэдра меньше ребра икосаэдра.  

Усечённый икосаэдр — это многогранник, который состоит из 12 правильных 5-ти угольников и 20 правильных 6-ти угольников. У усеченного икосаэдра икосаэдрический тип симметрии.   Примеры икосаэдров в мире: Обычный футбольный мяч является усечённым икосаэдром(рис 1) Капсиды большинства вирусов (например, бактериофаги, мимивирус(рис2)). Рис.1 Рис.2

Молекула фуллерена C6О — усечённый икосаэдр