Презентация на тему: Основы логики. Повторение

ОСНОВЫ ЛОГИКИПовторениеПодготовил учитель информатики и ИКТМОБУ «Ленинская СОШ№1 им. Борисова П.С.Антропова С.Ю.

логика НАУКА О ФОРМАХ И СПОСОБАХ МЫШЛЕНИЯ НАУКА О ФОРМАХ И СПОСОБАХ МЫШЛЕНИЯ Какие формы мышления вы знаете?

Понятия Понятия Высказывания Умозаключения Что такое понятие?

ПОНЯТИЕ форма мышления, которая выделяет существенные признаки предмета или класса предметов, позволяющие отличать их друг от друга форма мышления, которая выделяет существенные признаки предмета или класса предметов, позволяющие отличать их друг от друга (Пример: Прямоугольник - геометрическая фигура у которой все углы прямые и противоположные стороны равны) Приведите свой пример понятия Что такое высказывание?

ВЫСКАЗЫВАНИЕ формулировка своего понимания окружающего мира (повествовательное предложение в котором что-либо утверждается или отрицается) формулировка своего понимания окружающего мира (повествовательное предложение в котором что-либо утверждается или отрицается) (Пример: Париж – столица Франции) Приведите свой пример высказывания.

ВЫСКАЗЫВАНИЕ ИСТИННОЕ ЛОЖНОЕ ИСТИННОЕ ЛОЖНОЕ (Пример: Буква «А» - (Пример: Компьютер гласная) был изобретен до нашей эры)

УМОЗАКЛЮЧЕНИЕ форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение (знание или вывод) (Пример: любая теорема) Приведите свой пример умозаключения..

АЛГЕБРА ЛОГИКИ наука об общих операциях, аналогичных сложению и умножению, которые выполняются над высказываниями наука об общих операциях, аналогичных сложению и умножению, которые выполняются над высказываниями

Логическая переменная – это простое высказывание, содержащее только одну мысль Логическая переменная – это простое высказывание, содержащее только одну мысль Обозначение: латинская буква (А, В, Х …) Значение: ИСТИНА (1) или ЛОЖЬ (0) Логические операции – логическое действие Какие логические операции вы знаете?

Базовые логические операции

Таблица истинности таблица определяющая значение сложного высказывания при всех возможных значениях простых высказываний таблица определяющая значение сложного высказывания при всех возможных значениях простых высказываний

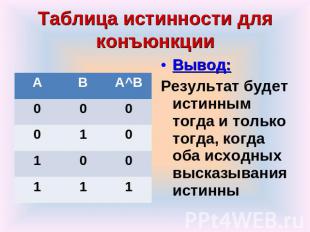
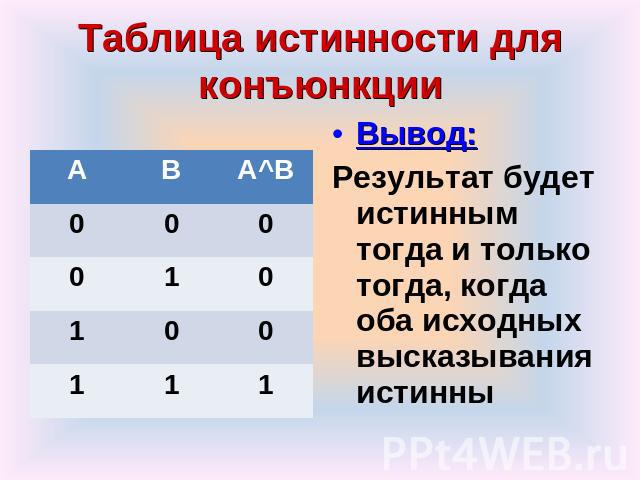
Вывод: Вывод: Результат будет истинным тогда и только тогда, когда оба исходных высказывания истинны

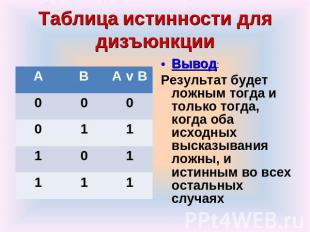
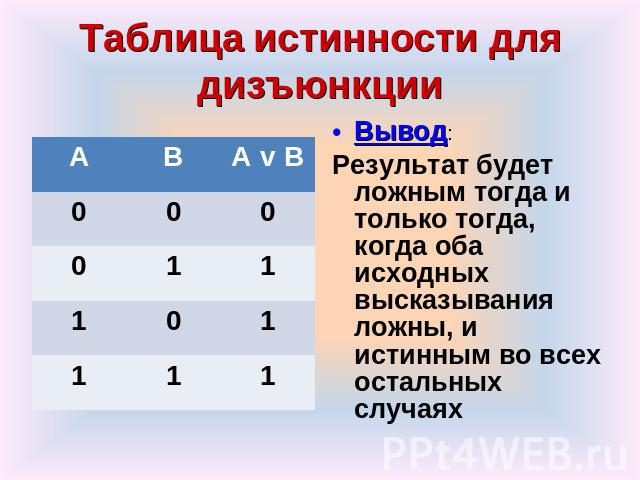
Таблица истинности для дизъюнкции Вывод: Результат будет ложным тогда и только тогда, когда оба исходных высказывания ложны, и истинным во всех остальных случаях

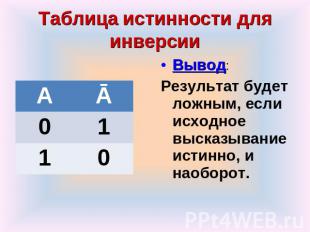
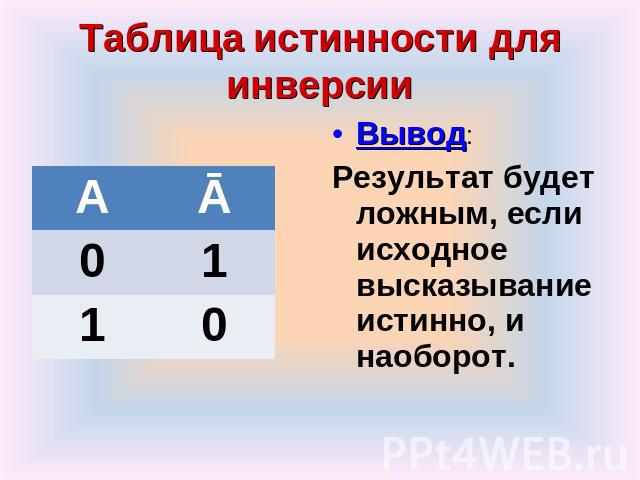
Таблица истинности для инверсии: Вывод: Результат будет ложным, если исходное высказывание истинно, и наоборот.

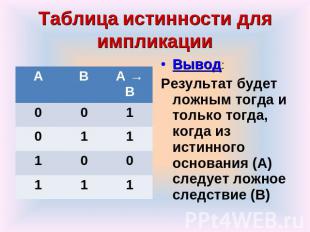
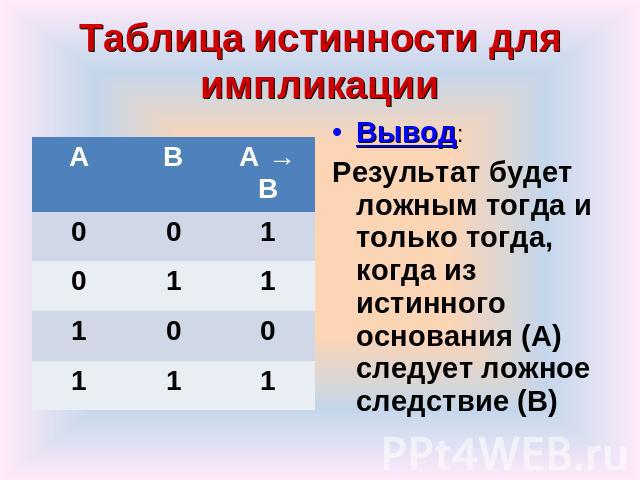
Таблица истинности для импликации Вывод: Результат будет ложным тогда и только тогда, когда из истинного основания (А) следует ложное следствие (В)

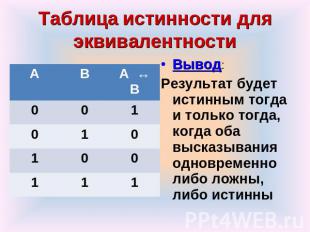
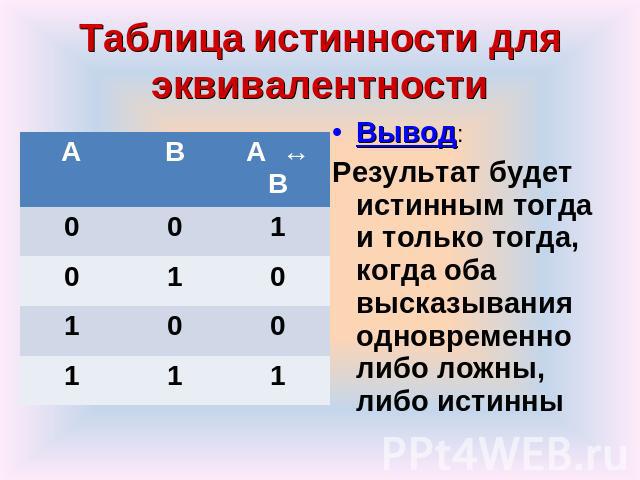
Таблица истинности для эквивалентности Вывод: Результат будет истинным тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны